辐射源信号模糊函数主脊切面特征优化

龙良将，张葛祥，田 波，王 庆

(西南交通大学电气工程学院，四川 成都 610031)

0 引言

自20世纪80年代以来，随着电子战的激烈对抗，复杂体制雷达不断投入使用，雷达信号的体制和调制样式变得越来越多样化［1］。仅靠传统的脉幅(pulse amplitude，PA)、脉宽(pulse width，PW)、载频(radio frequency，RF)、到达时间(time of arrival，TOA)和到达方向(direction of arrival，DOA)这5个参数分析和识别雷达信号已远远不能适应日益严峻的电子对抗环境［2-3］。为此，新一代电子对抗系统除继续利用这5个常规分选参数外，还必须具有提取和补充雷达信号新特征参数的能力［4-5］。

文献［1］利用模糊函数提供了对信号结构较为完整的描述，提出了一种提取模糊函数主脊(定义为过原点的模糊函数能量的主要分布带)切面特征的方法。该方法利用分数自相关(fractional autocorrelation，FA)等价于相应分数域上模糊函数径向切面的关系，通过分数自相关搜索模糊函数的主脊切面，并采用矩方法描述该主脊切面的特征分布信息，从而提取能够表征信号模糊函数能量分布特性的新特征参数。所提取的特征向量不仅能较好地反映不同信号波形在结构上的差异，且具有类内聚敛性强、类间分离度大和抗噪性能好等优点。但是文献［1］通过分数自相关搜索模糊函数的主脊切面时，为满足所需的精度，需在搜索区域内取步长很小的一定数量均匀离散值，因此，计算量特别大，限制了该方法的实际应用。文献［6］提出了一种新的算法，使其计算量大大减少，但该方法只对线性调频信号有效，因此具有一定的局限性。本文利用量子进化算法具有种群小，收敛速度较快，全局寻优能力强的特点，提出基于量子进化算法的模糊函数主脊切面快速算法。实验结果表明，该方法针对各种信号都有效，比文献［6］方法通用性强，且与文献［1］相比，其计算量大大减少。

1 模糊函数及其主脊切面

1.1 模糊函数

对于任意窄带雷达信号s(t)，其模糊函数定义为［7］

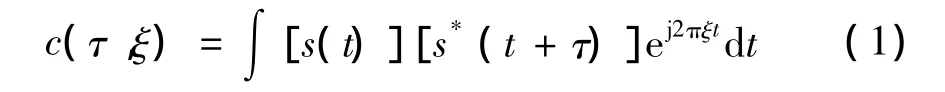
(1)式中:s*(t)为信号s(t)的共轭;t为时间;τ为信号时延;ξ为模糊函数，实质上是信号在时延τ和频移ζ平面上的联合二维时频表示。文献［8］中，Akay等基于算子方法定义了分数自相关运算，并指出分数自相关与模糊函数具有如下关系

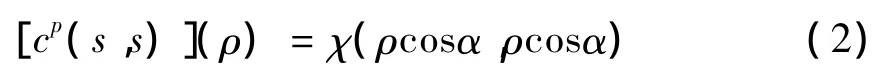
(2)式中:p为分数域阶数;α=pπ/2;cp为旋转角α的分数域uα上的分数相关算子;自变量ρ为uα域的径向距离;χ(·)为模糊函数。由(2)式可知，旋转角为α的分数域上的自相关等价于该分数域上模糊函数的径向切片，因此通过计算信号的分数自相关就可以得到模糊函数任意过原点的径向切面，这是一个非常重要的关系。Akay推导出分数自相关运算［8］为

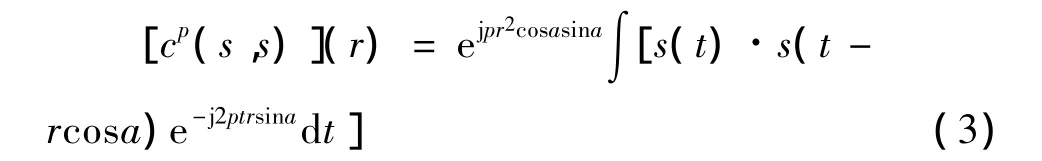
(3)式中:cp为相应的分数相关算子;r为分数域的径向距离。同时，利用算子处理方法，(3)式可进一步改写成为

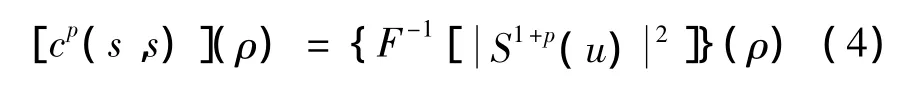
(4)式中:S1+p(u)为信号s(t)的1+p阶分数傅立叶变换;F－1为傅立叶逆变换。

1.2 模糊函数主脊切面

由AF唯一性定理和模糊函数体积不变特性可知，即使能量相同的2个信号，只要信号形式不同，那么它们的模糊函数主脊一般也显示出不同的特征［1］。(4)式为提取模糊函数的径向切面提供了便捷的方法，但为获取主脊切面仍需在一定的角度范围搜索。考虑到模糊函数的对称性，限制搜索范围为π/2，然后对固定的旋转角α作径向积分，构建如下检测量为

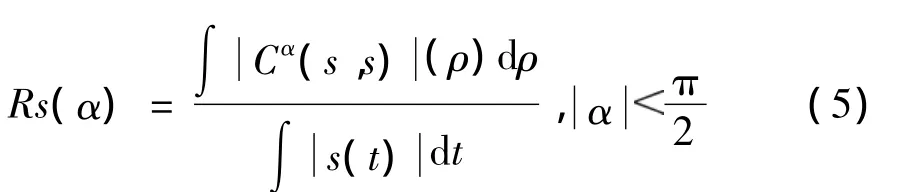
(5)式中，∫s(t)dt为归一化系数，目的是减少噪声和信号能量对Rs(α)取值范围的影响。于是根据(5)式求出最大值所对应的角度α'，则角度α'对应的切面即为模糊函数的主脊切面，同时给出相应的旋转角α'为

(6)式中，α'描述了模糊函数能量在二维时频面上的分布走向。

2 基于量子进化算法的主脊切面快速提取算法

由于搜索模糊函数主脊切面复杂度高，虽然文献［6］的方法能快速搜索主脊切面，但只对LFM信号有效，因此不具有通用性。考虑量子进化算法具有种群小，收敛速度快，全局寻优能力强的优点，本文提出一种基于量子进化算法的主脊切面快速提取算法，利用该算法对主脊切面所对应的旋转角α'进行寻优。

量子进化算法是量子计算与进化算法相融合的产物［9］。它以量子计算的一些概念和理论为基础，用量子位编码来表示染色体，量子门作用和量子门更新来完成进化搜索，具有种群规模小而不影响算法性能，全局寻忧能力强的特点［10］，从而实现了目标的优化求解。

2.1 量子染色体

在常规计算机中，经典信息比特单元用二进制来表示，它不是处于0态就是处于1态，而在二进制量子计算机中，信息比特单元称为量子位，它除了处于0态或1态外，还可处于二者的任意线性叠加态，0态和1态各以一定的概率同时存在，只有通过测量才呈现出确定的0态或1态。一个量子位的叠加态可用二维Hilbert空间单位向量 ψ〉描述为

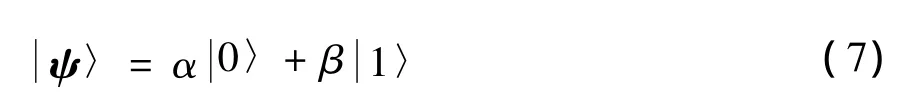
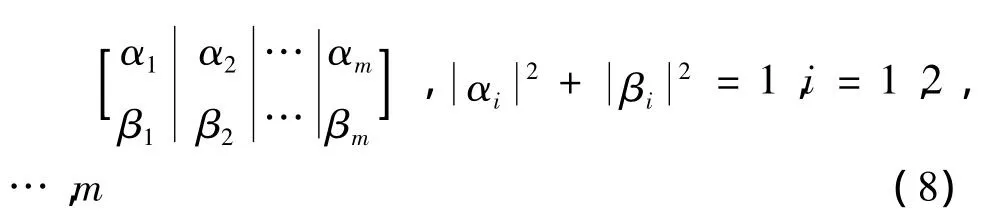
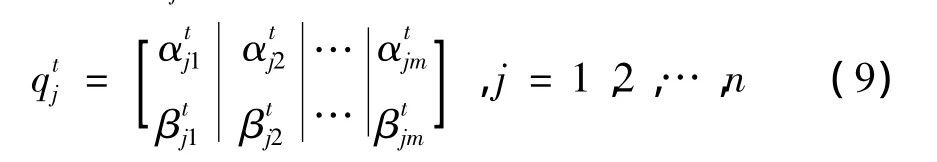
2.2 量子更新

量子进化算法中的更新算子是算法的关键，它取代了经典进化算法中交叉和变异的过程，在更新Q(t)这一步中，可以根据量子的叠加特性和量子变迁理论，运用一些合适的量子门来更新Q(t)。需要指出:由于概率归一化条件的需求，量子门变换矩阵必须是可逆的酉正矩阵，需要满足 U*U=UU*(U*为U的共轭转置)。常用的量子变换矩阵有:异或门、受控的异或门、旋转门和Hadamard门等。本文采用量子旋转门来更新Q(t)。更新采用的是量子旋转门作用于量子位，量子旋转门形式为

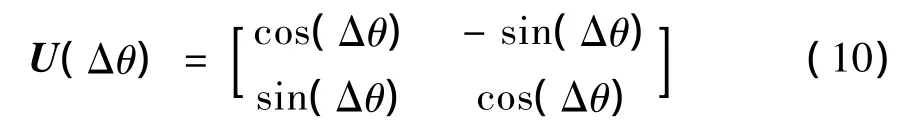
量子旋转门中的旋转角度Δθ由量子位、个体的观测值与当前最优解确定，可通过Δθ查询表确定［11］。量子位通过量子门更新为

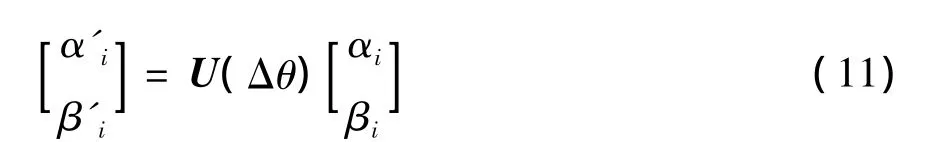
2.3 主脊切面快速提取算法流程

本文利用量子进化算法寻求最佳模糊函数主脊切面，需要先对主脊切面参数进行量子染色体的编码以及种群的初始化，这里的参数是角度α，且搜索范围为π/2。再通过观测和解码，将量子染色体变换到变量空间，将(6)式作为目标函数，进而进行适应度值的评价，保存最优个体的信息，以最优个体的信息为引导，利用量子旋转门实现种群的进化。算法的详细流程如下。

1)首先设代数t=0，产生初始种群Q(t)，初始种群中，个体是所有状态的等概率线性叠加，即所有个体中的α和β均设置为1/;

2)对初始化种群Q(0)中的个体进行观测，得到观测种群 p(0)={，，…}，观测种群中个体均为确定的二进制串;

3)利用适应度函数(6)式评价p(0)中各观测个体，并将最佳个体状态及其适应度值记录于P_best和f_best中;

4)while非结束状态do

begin

①t=t+1;

③利用适应度函数(6)式评价p(t)中各观测个体;

④利用量子旋转门更新Q(t);

⑤记录最佳个体:用p(t)与P_best中的最优解替代当前的全局最优解P_best，并将P_best个体适应度值替代f_best中的值。

end end

3 仿真及结果分析

现选取线性调频信号(linear frequency modulation，LFM)、二相编码(binary phase shift keying，BPSK)、四相编码(quadrature phase shift keying，QPSK)、常规信号(conventionality pulse，CON)、二频率编码(frequency-shift keying，FSK)共5种典型信号进行仿真对比实验。其中，LFM的带宽为15 MHz，BPSK采用13位Barker码，QPSK则采用16位Frank码。所有信号的脉宽PW为10 μs，抽样频率fs为60 MHz，除了FSK信号的2个频率分别取10 MHz和2 MHz外，其余4种信号的载频 RF为10 MHz。以fs对这5种信号进行常规采样，得到600个离散点，为了加快分数自相关的计算，再对离散信号重采样，重采样后的数据点为1 024，限制搜索角度为π/2，1。利用量子进化算法求解模糊函数主脊切面，也即是对最佳旋转角α'=argmaxRs(α)进行优化，本实验计算最大代数为50代，每代个体数为20，每个个体量子比特数为22。文献［1］求信号的模糊函数主脊切面时，在其搜索角度取值区间内取L个均匀离散值，要得到比较精确的搜索结果，就需要采用很小搜索步长，从而搜索次数L变得很大，文献［1］中L取值为1 800。量子进化算法和文献［1］这2种方法获得的上述5种信号主脊切面结果如图1和图2所示。为简单起见，文献［6］方法只对LFM，BPSK，QPSK这3种信号主脊切面进行提取，结果如图3所示。再利用量子进化算法和文献［1］对5种信号分别做了10次仿真实验，在利用量子进化算法对5种信号进行仿真时，每种信号达到稳定状态时所花平均时间和文献［1］所花平均时间的比较如表1所示。对LFM信号计算50代所得的某一次实验结果如图3所示。LFM信号的进化代数如图4所示。

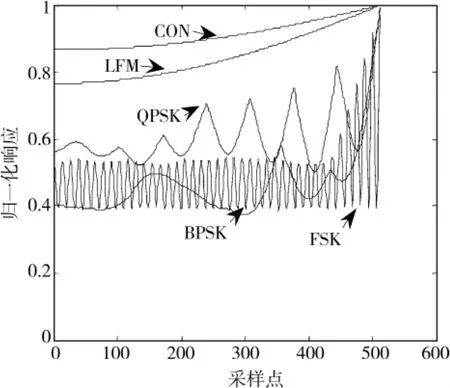
图1 量子进化算法搜索的5种信号主脊切面图Fig.1 Main ridge slices of 5 signals in QEA

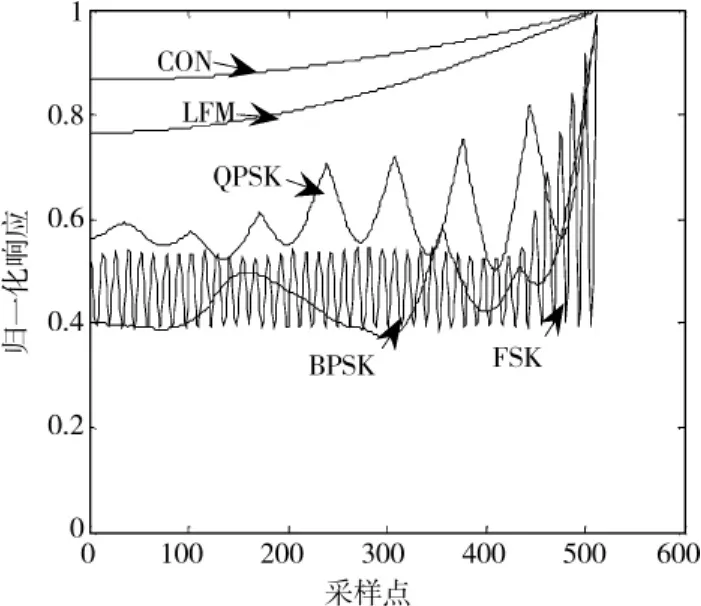
图2 文献［1］搜索的5种信号主脊切面图Fig.2 Main ridge slices of 5 signals in［1］

从仿真结果可以看出，量子进化算法比文献［6］所提方法通用性强，文献［6］所提方法只适用于LFM信号。从图1与图2可以看出，量子进化算法与文献［1］所得5种信号主脊切面的精度基本相同，但由表1可以看出，利用量子进化算法所需平均时间要比文献1方法所需时间大大减少。通过比较可知，量子算法要优于其他2种算法。

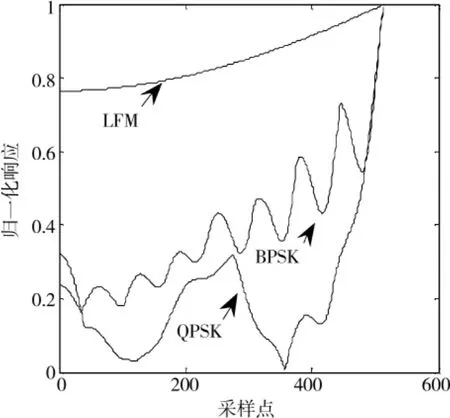
图3 文献［6］搜索的3种信号主脊切面图Fig.3 Main ridge slices of 3 signals in［6］

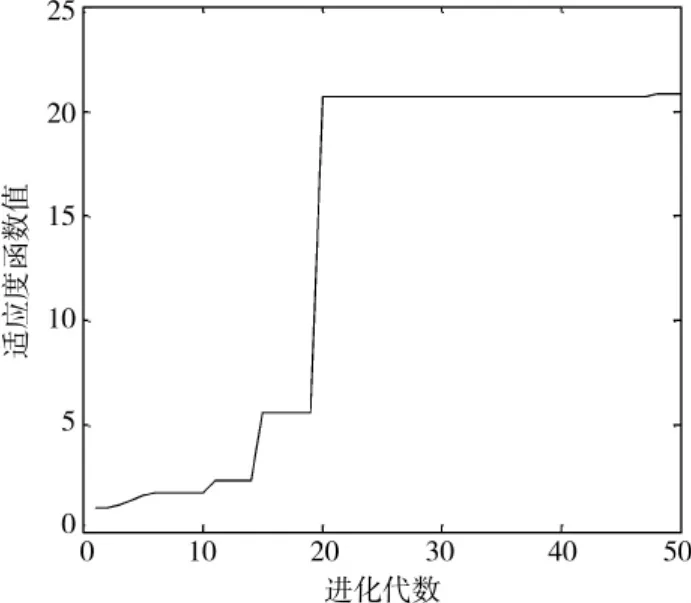
图4 LFM信号进化代数图Fig.4 Evolution of the number of LFM

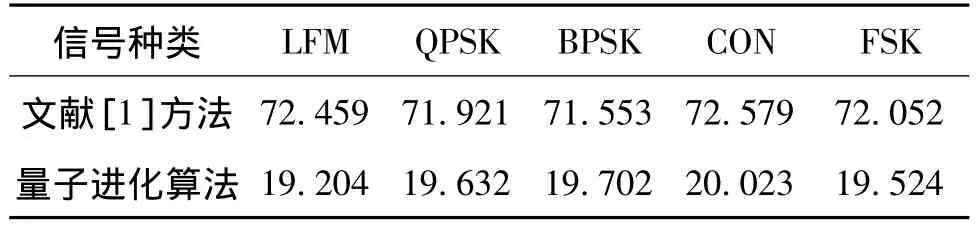
表1 量子进化算法与文献［1］所花时间的比较Tab.1 Comparisins of consumed time between the QEA and the approach in［1］

4 结论

由于搜索模糊函数主脊切面复杂度很高，因此快速、精确提取主脊切面是一个值得研究的方向。本文简要介绍了量子进化算法后，提出了基于量子进化算法的模糊函数主脊切面优化算法。该算法充分利用了量子进化算法种群规模小、收敛速度快，能够较快地发现最优解的优点，快速搜索模糊函数主脊切面。

［1］普运伟，金炜东，朱明，等.雷达辐射源信号模糊函数主脊切面特征提取方法［J］.红外与毫米波学报，2008，27(2):133-138.PU Yunwei，JIN Weidong，ZHUming，et al.Extracting the main ridge slice characteristics of ambiguity function for radar emitter signals［J］.Journal of Infrared and Millimeter Waves，2008，27(2):133-138.

［2］巫胜洪.雷达脉内特征提取方法的研究［J］.舰船电子对抗，2002，25(1):25-28.WU Shenghong.Research of radar emitter signals intrapulse feature extraction method［J］.Shipboard Electronic Warfare，2002，25(1):25-28.

［3］沙祥.脉内分析综述［J］.现代电子，1998，65(4):1-8.SHA Xiang.The Review of intrapulse analysis［J］.Modern Electronics，1998，65(4):1-8.

［4］张葛祥，胡来招，金炜东.雷达辐射源信号脉内特征分析［J］.红外与毫米波学报，2004，23(6):476-480.ZHANG Gexiang，HU Laizhao，JIN Weidong.Intrapulse feature analysis of radar emitter signals［J］.Journal of Infrared and Millimeter Waves，2004，23(6):476-480.

［5］朱明，金炜东，普运伟，等.基于Chirplet原子的雷达辐射源信号特征提取［J］.红外与毫米波学报，2007，26(4):302-306.ZHU Ming，JIN Weidong，PU Yunwei，et al.Feature extraction of radar emitter signals based on Gaussian Chirplet atoms［J］.Journal of Infrared and Millimeter Waves，2007，26(4):302-306.

［6］龙良将，张葛祥，田波，等.一种搜索LFM信号模糊函数主脊切面的快速算法［J］.重庆邮电大学学报:自然科学 版，2010，22(1):33-36.LONG Liangjiang，ZHANG Gexiang，TIAN Bo，et al.A fast algorithm for extracting main ridge slice of ambiguity function of LFM signal［J］.Journal of Chongqing University of Posts and Telecommunications:Natural Science E-dition，2010，22(1):33-36.

［7］林茂庸，柯有安.雷达信号理论［M］.北京:国防工业出版社，1984.LIN Maoyong，KE Youan.Theory of radar signal［M］.Beijing:National Defense Industry Press，1984.

［8］AKAY Olcay，BOUDREAUX Bartels G Fave.Fractional Convolution and Correlation via Operator Methods and an Application to Detection of Linear FM Signals［J］.IEEE Trans on Signal Processing，2001，49(5):979-993.

［9］王凌.量子进化算法研究进展［J］.控制与决策，2008，23(12):1321-1326.WANG Ling.Advances in quantum-inspired evolutionary algorithms［J］.Control and Decision，2008，23(12):1321-1326.

［10］张葛祥，李娜，金炜东，等.一种新量子遗传算法及应用［J］.电子学报，2004，32(3):476-479.ZHANG Gexiang，LI Na，JIN Weidong，et al.A novel quantum genetic algorithm and its application［J］.Acta Electronica Sinica，2004，32(3):476-479.

［11］陈明.量子进化算法研究及应用［D］.长沙:湖南师范大学，2007.CHEN Ming.Research of Quantum inspired evolutionary algorithm and its application［D］.Changsha:Hunan Normal University，2007.