不均衡数据分类算法的综述

陶新民，郝思媛，张冬雪，徐 鹏

(哈尔滨工程大学信息与通信工程学院，黑龙江 哈尔滨 150001)

0 引言

分类问题是数据挖掘领域中重要的研究内容之一。传统的分类方法对平衡数据集分类取得了良好的效果。但实际的数据集往往不平衡，即数据集中某类的样本数远远大于其他类的样本数目。对于基于总体分类精度为学习目标的传统分类器而言，这种不均衡势必会导致分类器过多关注多数类样本，从而使少数类样本分类性能下降。而在实际应用中，人们更关心的恰恰是数据集中的少数类，并且错分这些少数类的代价也通常大于多数类，例如，把有入侵行为判为正常行为，将有可能造成重大网络安全事故;把癌症病人误诊为正常，将会延误最佳治疗时机，对病人造成生命威胁;将故障误判为正常，导致故障漏检，有可能引发重大安全事故。因此，在实际应用中，人们更需要提高少数类样本的分类精度。

对不均衡样本机器学习的研究已成为目前最热门的课题之一［1-2］，近年来，一些重要的学术会议都对不均衡样本分类进行了讨论与分析。例如:由美国人工智能协会主办的关于不均衡样本学习的研讨会(AAAI'00)［3］，不均衡样本集机器学习的国际会议研讨会(ICML'03)［4］，计算机机械专家组主办的知识发现和样本挖掘探索协会(ACMSIGKDD'04)［5］等。这些对不均衡样本学习问题的关注和研讨活动促进了该研究领域的快速发展，使得与该领域的有关论文呈明显增长趋势。由于研究该领域的重要性且该领域发展的迅速性，有必要将该领域近年来的研究成果进行整理和总结，并对该领域今后的发展提出设想和展望。

1 不均衡数据分类问题的本质

数据不均衡表现在两个方面。

一方面为类间不均衡，即某类样本数量明显少于其他类样本数量。由于传统分类器都是以总体分类精度为学习目标，因此在这种情况下，为了获得更大的分类精度，训练算法势必会导致分类器过多关注多数类样本，从而使少数类样本分类性能下降。例如对于一个99∶1的不均衡数据分类问题而言，分类器在把少数类样本完全误判为多数类情况下，所获的总体分类精度仍然很高，即为99%，而此时少数类样本的错分率却是100%。

另一方面在多数类与少数类出现类间不均衡的同时，在每一类样本中间也可能存在另一种不平衡的形式，即类内不均衡［6-11］。大量研究表明，样本间不均衡的程度不是阻碍分类学习的唯一因素，类内的不均衡也是导致分类性能恶化的重要因素，如图1，2所示。其中三角和空心椭圆分别代表少数类和多数类。图1和图2中的分布都存在类间不均衡，不过图1中，类间没有重叠的样本，且每一类都只有一个聚类。但是，在图2中不仅有多个子集，同时还有重叠的样本。类内不均衡问题实质上与数据集内存在分离项密切相关。研究表明，小的分离项的存在会导致分类器性能严重下降。简单说，分类器试图通过描述占主要地位的聚类来建立学习规则，必然会导致该规则缺乏对次子集的描述［12-14］。由于分类器既要学习少数类又要学习多数类，少数类次子集的出现可能会导致多数类产生小的分离项，从而增加了分类器的学习难度。此外，由于缺乏少数类样本，分类器无法有效分辨出少数类样本噪声和少数类样本子集。例如，在图2中，设想对于集B中的2个少数类噪声样本，分类器可能产生相应的小分离项，然而分类器很难将由噪声产生的非法分离项与合法子集C区分开来，这些都是导致传统分类器学习性能下降的主要原因。

2 不均衡数据分类的改进算法

近年来，很多学者针对不均衡数据分类问题提出了多种改进算法。改进方向主要归纳为以下两类:一是从数据集的角度，另一个是从算法角度。

图1 类间不均衡数据集Fig.1 Unbalanced between classes

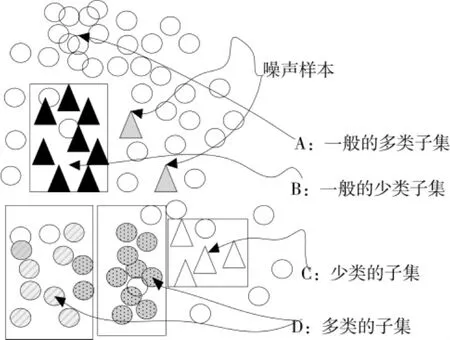
图2 既有类间，又有类内不均衡的高复杂度的数据集Fig.2 Highly complicated dataset with unbalanced of classes and the class

2.1 数据集层面的方法

数据层面的处理方法是通过一些机制改善不均衡数据集，以期获得一个均衡的数据分布。它是处理不均衡数据分类问题的重要途径之一，因为与不均衡的数据集相比，一个均衡的数据集更有利于提高全局的分类性能［15-16］。

2.1.1 过抽样策略

随机过抽样是处理不均衡数据最基本的方法。该算法首先复制随机选择的少数类样本，并将生成的样本集合添加到少数类中，得到新的少数类集合。虽然它只是简单地将复制后的数据添加到原始数据集中，且某些样本的多个实例都是“并列的”，但是也有可能使分类器学习出现过拟合现象［17］。特别是，过抽样算法会导致分类器对于同一个样本的多个复本产生多条规则，从而使这些规则过于具体化。为了有效解决随机过抽样算法的过拟合问题，Chawla N V等提出了一种基于人工合成少数类过抽样技术(synthetic minority over-sampling technique，SMOTE)。SMOTE算法的基本思想是:首先寻找每一个少数类样本的k个同类最近邻样本(其中k通常是大于1的奇数)，然后随机选择k个最近邻中的一个，并在这2个样本之间随机进行线性插值，构造出新的人工少数类样本。该方法可以有效地解决由于决策区间较小导致的分类过拟合问题，而且可使分类器的学习能力得到显著提高。但是，SMOTE算法对每个原少数类样本产生相同数量的合成数据样本，而没有考虑其邻近样本的分布特点，使得类间发生重复的可能性加大［18］。另外，SMOTE算法的样本生成机制也同样存在一定的盲目性。为了克服上述不足，近些年一些学者相继提出了许多针对SMOTE的改进算法，例如文献［19］提出的利用求最近邻样本均值点进而生成人工样本的D-SMOTE算法;文献［20］利用周围空间结构信息的邻居计算公式提出的N-SMOTE过抽样算法;文献［21］提出的基于交叉算子的过抽样算法以及文献［22］提出的基于核SMOTE的过抽样方法。此外，还有一些自适应过抽样方法相继被提出，具有代表性的算法包括Borderline-SMOTE算法［23］和自适应合成抽样算法 (adaptive synthetic sampling，ADASYN)［24］。SMOTE算法和这些自适应抽样算法最大的差别在于:SMOTE算法为每一个少数类样本生成合成样本，而Borderline-SMOTE算法只为那些“靠近”边界的少数类样本生成合成样本，而ADASYN算法的主要思想是使用密度分布作为自动确定合成样本数目的标准，且通过自适应地改变不同少数类样本的权重，为每个样本产生相应数目的合成样本。

另外，为了解决SMOTE技术引起的噪声样本问题，一些数据清洁技术也已被广泛采用，最具代表性的是SMOTE与Tomek算法相结合的SMOTE+Tomek算法［25］，该算法首先利用SMOTE算法生成合成样本，然后利用Tomek算法对来自2个不同类的Tomek连接样本对进行清理，这样就很好地克服了SMOTE带来的噪声问题。

除了采用SMOTE合成人工样本外，一些学者还提出利用概率密度生成第二类人工数据的方法。该方法是利用合适的概率分布来生成异性样本，然后通过将不均衡数据问题转换为均衡两类问题，实现不均衡数据的分类。如文献［26］提出的均匀分布，以及文献［27］提出的基于高斯分布产生第二类数据的方法。然而，在众多的复杂实际问题中，异性样本有很多种，分布十分复杂，不可能通过单一的概率模型对其进行描述。为此，文献［28］提出一种基于阴性免疫的过抽样算法，该算法利用阴性免疫算法对多数类样本学习，生成覆盖少数类样本空间的人工少数类样本，从而实现训练样本数据的均衡。由于该算法只利用多数类样本先验知识，不需要少数类样本信息，因此避免了通过学习少数类样本生成的人工样本缺乏空间代表性的不足。由于在不均衡数据应用中，多数类样本数据很容易得到，因此该算法具有广阔的应用前景。

2.1.2 欠抽样策略

与过抽样技术将数据添加到原始数据集的机制不同，欠抽样技术是将数据从原始数据集中移除。最基本的欠抽样技术是随机欠抽样，即随机地减少多数类样本来缩小多数类样本的规模，达到与少数类样本数量相同的目的。但是该方法在将多数类样本删除的同时有可能会丢失具有代表性的多数类样本信息。为克服这一不足，文献［29］提出2个Informed的智能欠抽样算法:EasyEnsemble和 BalanceCascade算法。其中EasyEnsemble算法的实施方法很简单:通过从多数类中独立随机抽取若干子集，且将每个子集与少数类数据联合起来训练生成多个基分类器，最终将这些基分类器组合形成一个集成学习系统。BalanceCascade算法则使用前面已形成的集成分类器来为下一次训练选择多数类样本，然后再进行欠抽样。与此同时，P.Chan 等［30］提出了一种最近邻规则欠抽样方法(edited nearest neighbor，ENN)，基本思想是删除其最近的3个近邻样本中的2个或者2个以上类别不同的样本。但是大多数的多数类样本附近的样本都是多数类的，所以该方法所能删除的多数类样本十分有限。鉴于此，Laur Ikkala J等［31］在ENN的基础上提出了邻域清理规则欠抽样方法(neighborhood cleaning rule，NCL)，核心思想是针对训练样本集中的每个样本找出其3个最近邻样本，若该样本是多数类样本且其3个最近邻中有2个以上是少数类样本，则删除它;反之，当该样本是少数类，并且其3个最近邻中有2个以上是多数类样本，则去除近邻中的多数类样本。但是该方法中未能考虑到在少数类样本中存在的噪声样本，而且第2种方法删除的多数类样本大多属于边界样本，对后续分类器的分类会产生很大的不良影响。鉴于此，文献［32］使用K-近邻(K-nearest neighbor algorithm，KNN)分类器来进行欠抽样，并给出4种不同的KNN欠抽样方法，即:NearMiss-1，NearMiss-2，NearMiss-3以及“最远距离”方法。其中，NearMiss-1方法选择到最近的3个少数类样本平均距离最小的那些多数类样本;而NearMiss-2方法选择到最远的3个少数类样本平均距离最小的那些多数类样本;NearMiss-3为每个少数类样本选择给定数目的最近多数类样本，目的是保证每个少数类样本都被一些多数类样本包围;“最远距离”方法则选择到最近的3个少数类样本平均距离最大的那些多数类样本。除上述方法外，还存在其他类型的智能欠抽样方法，如Kubat等［33］提出的单边选择方法(one-sided selection，OSS)，该方法是将多数类样本分为“噪音样本”、“边界样本”和“安全样本”，然后将边界样本和噪音样本从多数类中删除，尽可能保留那些具有一定信息量又有一定空间代表性的样本。基于上述思想，文献［34-35］提出利用聚类方法来获得具有空间代表性的样本。算法首先对多数类样本进行聚类，聚类个数设置与少数类样本数目相同，然后提取出每个聚类的中心作为多数类样本，如此操作就可以使选择出来的多数类样本具有一定的空间代表性，典型的聚类方法有谱聚类和核聚类方法。

由上述分析可知，过抽样算法采用的是重复少数类样本或生成人工样本的方式实现样本均衡，这样会增加训练时间，且容易产生过拟合现象。而欠抽样算法采用的是删除多数类样本的方式实现样本均衡，容易导致丢失重要的样本信息。因此，为了弥补欠抽样和过抽样的缺点，文献［36］提出基于随机欠抽样和SMOTE相结合的不均衡SVM分类算法以及文献［37］提出逐级优化递减(optimization of decreasing reduction，ODR)欠抽样算法和BSMOTE算法相结合的不均衡SVM分类算法。该方法的核心是:首先利用ODR对多数类样本进行欠抽样，去除样本中大量重叠的冗余和噪声样本，使得在减少数据的同时保留更多的有用信息;而对少数类样本的过抽样则是对边界样本进行的，如此操作能更有利于后续SVM算法分类界面的生成，最终实现提高不均衡数据SVM算法分类性能的目的。

2.2 算法层面的方法

2.2.1 改变概率密度

由于目标(正常)样本已知，可以通过采用合适的统计分布来实现目标样本的概率密度估计，在识别阶段，依据得到的概率密度，若其他样本的概率密度值低于某个预先设定的阈值，则认定为异性样本。如文献［38］采用高斯分布进行目标样本密度估计。该方法的最大问题是对所选的统计模型十分敏感，需要人们事先了解目标样本的分布，这在很多现实应用中难以实现。另一种方法是采用无参数概率密度方法，如文献［39-40］提出的基于核空间密度估计不均衡数据分类方法，该算法由于将密度估计从传统数据空间转换为高维核空间中进行，有可能导致算法出现维度灾难问题且计算复杂度也大大提高。因此，这种方法在实际应用中还是存在很大限制。

2.2.2 单类学习分类

基于单类学习的分类算法是将传统不均衡数据基于区别的分类方法改为基于识别的方法进行学习。其主要思想是只利用感兴趣的目标类样本进行学习和训练，即只对多数类样本进行训练，其目标是从测试样本中识别出多数类样本，而不是对少数类和多数类进行区分。对于新的样本，通过比较该样本与目标类的相似程度来识别该样本是否归属于目标类。如文献［41-42］采用支持向量机数据描述方法实现目标数据的非线性边界描述。

2.2.3 集成算法(ensemble learning)

从20世纪90年代开始，对集成学习理论和算法的研究成为了机器学习的一个热点。早在1997年，国际机器学习界的权威 T.G.Dietterich就将集成学习列为机器学习4大研究方向之首，典型的集成方法有:Bagging［43］、随机森林［44］和 Boosting。

1)Boosting。

AdaBoost算法是Boosting中最具代表性的算法，基本思想是:集中在上次分类器判决出错的样本。开始时，每一个样本给定固定的权重，一般采用均匀分布，每次循环后，产生一个新的分类器，然后重新对训练样本进行加权，使下一个训练分类器集中在上次最近的分类器判别出错的训练样本上，即出错的样本施加更大的权重，易分样本减少权重，最后利用加权投票集成方法实现决策分类［45］。由于在不均衡数据分类应用中容易将少数类样本错分，因此集成算法就会过多地关注少数类样本，从而产生有利于少数类分类的基分类器，最终通过集成实现提高分类器对少数类的分类性能。

2)抽样和集成算法的融合。

抽样策略与集成学习算法相融合的思想已在不均衡数据分类领域中广泛应用。例如，文献［46］提出的DataBoost-IM算法，它是将文献［47］提出的数据生成技术与AdaBoost.M1结合，根据类间难以学习样本的比例生成合成样本;另一种算法是文献［48］提出的SMOTEBoost算法，它是基于SMOTE抽样技术和Adaboost.M2算法相融合的思想。该算法是在每次boosting迭代中引入了合成抽样技术。这样，每个连续的分类器就更加注重少数类，由于每个基分类器都建立在不同的数据样本上，最终投票集成后的分类器就会使得少数类拥有更宽广、更明确的决策域。

虽然合成抽样方法可有效解决不均衡数据的学习问题，但是由于数据生成方法都相对复杂，且计算量很大。为此，针对随机过抽样技术中导致的数据重叠问题，Mease et al.在文献［49］中提出了能克服这一缺点的简单有效的过抽样技术，它不再使用计算方法生成新的数据，而是通过从随机过抽样获得重复数据且给新产生的重叠数据引入骚动(抖动)方法来打破这种重叠关系，这样就会使算法的运算效率大大提升，这就是著名的抖动过/欠抽样算法(over/under-sampling and jittering of the data，JOUSBoost)。该算法在每次boosting迭代中都向少数类样本引入独立的、同分布的噪声。这一思想较合成抽样方法来说相对简单，且能够结合Boost集成算法的优点来提高不均衡分类器的性能。类似的方法还有很多，例如文献［50］提出基于核函数的Adaboost分类算法，分别引入了3种核函数(多项式核函数、径向核函数、Sigmoid核函数)同Adaboost算法集成。文献［51］提出一种基于核的模糊多球分类算法及其集成算法。该算法在训练时，为每一个模式建造多个最小超球体覆盖所有的训练样本，在识别阶段利用隶属度函数对测试样本进行归类，最后将这些基分类器进行集成。为了提高样本的代表性以及分类器的泛化性能，文献［52］提出了基于核聚类欠抽样集成不均衡SVM分类算法，该算法首先在核空间中对多数类样本集进行聚类，然后随机选择出具有代表意义的聚类信息点，在减少多数类样本的同时，将SVM算法的分类界面向多数类样本方向偏移，并利用集成手段对基于核聚类的欠抽样SVM算法进行集成，最终实现提高不均衡数据SVM算法泛化性能的目的。

2.2.4 代价敏感学习

抽样技术是通过改变数据分布中类样本代表比例的方式实现数据均衡，而代价敏感学习方法则是通过考虑与错分样本相关代价的方式来处理不均衡分类。以往研究表明，代价敏感学习与不均衡数据学习有很大的联系，因此代价敏感方法的理论基础和算法很自然地被用到不均衡学习问题中，而不再需要通过抽样技术来建立均衡的数据分布。代价敏感学习使用的是特定的错分样本代价矩阵来处理不均衡学习问题，此外，很多实验表明，在一些应用领域，包括某种具体的不均衡学习领域，代价敏感学习都优于抽样方法。

代价敏感学习方法的基础理论是代价矩阵。代价矩阵可以看作是将一类样本错分为另一类样本惩罚项的数字表示。代价敏感学习算法有很多，一般说来可分成三类。第一类是将错分代价直接应用到数据集上作为数据空间的权重形式，利用错分代价选择最佳的训练分布，该技术称作代价敏感数据空间权重方法;第二类是将最小化代价技术应用到集成方法结合方案中，将标准的学习算法与集成方法相融合形成代价敏感集成分类器。这两类方法都有坚实的理论基础，代价敏感数据空间权重方法是基于转化定理的，而代价敏感集成分类器则是基于元代价框架的基础上。最后一类是将代价敏感函数或特征直接应用到分类实例中，使代价敏感框架直接融入到这些分类器中。典型算法有文献［53］提出的通过改变训练集类别分布的代价敏感性学习算法;文献［54］提出的通过改变正类和反类占总样本数比例的较优代价敏感分类器算法;文献［55］提出的代价敏感的支持向量机算法，该算法首先利用边界人工少数类过抽样技术(BSMOTE)实现训练样本的均衡，然后利用K近邻构造代价值，并利用每个样本的代价函数来消除噪声样本对SVM算法分类精度的影响。需要说明的是，在现实中，代价敏感学习方法通常难以确定代价敏感值的大小。因此，如何确定代价矩阵是阻碍该方法成功应用的关键。

2.2.5 核方法

随着SVM理论的快速发展以及成功应用，核方法越来越引起了人们的关注。线性SVM能够成功推广到非线性空间，就是得益于核矩阵能代替复杂内积计算的优势。针对不均衡数据分类问题，很多学者试图从核函数角度出发进行了研究，其中包括Wu和Chang［56］提出的一种通过修改SVM核矩阵的方法。该方法通过将核函数矩阵进行保角变换，实现扩大稀有类特征向量处的边界，增加正负类样本的分离度，减少大类支持向量数目的目的。文献［57］提出改进的基于核密度估计的数据分类算法。该方法通过引入空间信息和相应平滑参数，改善了原方法对不平衡问题的适应力。文献［58］提出利用特征选择方法来处理不均衡数据，使用多个朴实贝叶斯函数以及正规化逻辑回归作为分类器，实验结果表明，根据不均衡数据的成分将少数类特征和多数类特征结合，可以有效提高算法的分类性能。

以上方法都是针对单核情况进行分析的，然而采用单核进行映射的方式对所有样本进行处理并不合理。近年来，出现了大量关于核组合方法的研究，即多核学习方法。处理不均衡数据的典型多核算法是多尺度核的学习，直观思路就是进行多尺度核的序列学习［59］。多尺度核序列合成方法相当简单，它首先用大尺度核拟合对应决策函数平滑区域的样本，然后用小尺度核拟合决策函数变化相对剧烈区域的样本，后面的步骤利用前面步骤的结果，进行逐级优化，最终得到更优的分类结果。

3 不均衡数据分类器性能评价标准

传统的性能评估都是从分类器的整体分类情况来考虑，即考虑所有样本的分类准确率。但是在不均衡数据分类中，少数类样本更容易错分，同时少数类样本数目所占比例不大，所以总体分类性能的指标变化也不大。例如一个二分类的问题:A样本数目是99个，B样本数目是1个，按照传统性能评估指标(即总体的分类正确率)评估分类器的性能，分类器可以将所有样本都识别为A类，而总体的性能指标仍为99%。但是这就导致B类样本的错分概率为100%。在大多现实应用中，少数类样本识别率往往更为重要，因此，针对传统的性能指标存在的缺陷，很多学者在研究不均衡数据集分类时通常不使用总体分类性能指标，而使用以下几个性能指标。

定义在不均衡数据集中少数类样本为P;多数类样本为N;FP是指将多数类样本错分成少数类的数目;FN是指将少数类样本错分成多数类的数目;TP和TN分别表示少数类和多数类样本被正确分类的数目，具体如表1说明。

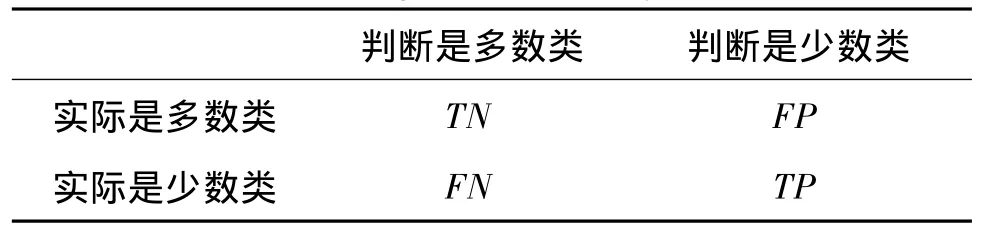
表1 二分类数据集的混合矩阵Tab.1 Mixing matrix of binary data sets

由此可以得到以下公式。少数类样本正确率为

从(4)式可知，性能指标G综合考虑了少数类和多数类两类样本的分类性能，G的值是随着少数类和多数类样本正确率在［0，1］单调递增的，因此要使G的值大，必须满足少数类和多数类样本正确率的值同时都大。如果分类器分类偏向于其中一类就会影响另一类的分类正确率，导致G值会变小。性能指标F也是一种常用的不均衡数据分类问题的评价准则。从(5)式中可知，性能指标F既考虑少数类样本的查全率又考虑查准率，其中任何一个值都能影响F值的大小。如果查全率和查准率的值都比较小，则F的值也会很小;若查全率较大而查准率较小，或者查全率较小而查准率较大，则F的值也都是很小;只有在查全率和查准率的值都比较大的前提下，F值才会很大。因此，可见该性能指标主要是在查全率和查准率均衡的情况下才可能将其最大化。它能综合地体现出分类器对多数类和少数类的分类效果，但侧重于体现少数类样本的分类效果。曲线下面积(area under the ROC curve，AUC)是另一个有效的不均衡数据分类性能评价手段，对于一个给定的两分类问题，ROC曲线是利用多个(FPR，TPR)对描述性能的方法，其中FPR代表假阳性率，TPR代表真阳性率，AUC是这个曲线形成的面积，如图3中着色部分。它评测的是FPR所有可能值对应的分类方法的性能，因此被证明是一个非常有效的不均衡分类性能评测标准。

4 几种主要学习方法的性能比较

4.1 实验数据

选用国际机器学习标准数据库UCI中的6个不同的数据集对算法进行实验，数据特征信息如表2所示，类别表示选择出来作为少数类和多数类样本的代表类别，例如，B∶A表示违约客户与不违约客户的个数比;R∶N表示复发病人和未复发病人个数比;NUC∶CYT表示细胞核与细胞质样本个数比。这里选择传统SVM分类算法作为分类器。

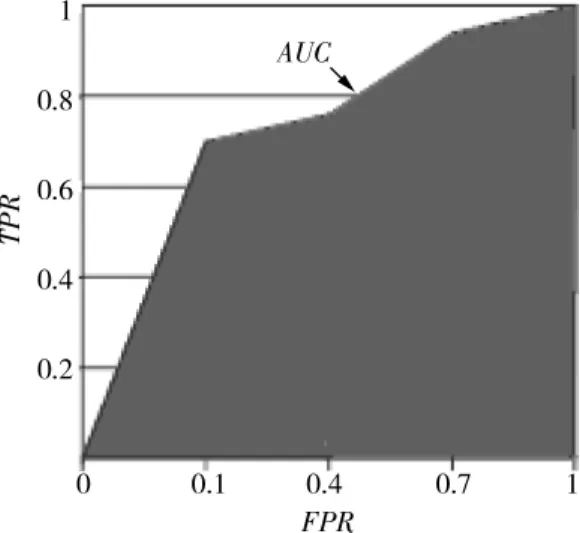
图3 ROC曲线示例Fig.3 ROC curve example

表2 实验数据集描述Tab.2 Description of experimental datasets

4.2 不同学习方法的分类性能比较

实验中，选取了几种具有代表性的学习方法进行比较，分别是:传统的SVM算法、基于随机欠抽样的SVM算法(RU)、基于SMOTE过抽样的SVM算法、基于BSMOTE过抽样的SVM算法、基于代价敏感的SVM算法(SVM-WEIGHT)和自适应人工样本过抽样SVM算法(AdaSyn)。对每一个数据集，采用10次交叉验证的方法进行实验，对每次交叉实验运行10次，以防止随机影响，最后计算这些实验的F，G性能评测指标的统计平均值。为了考察不均衡数据下，算法的分类性能，实验中选择1∶10的比例进行随机选择。其中，分类器SVM参数设置为:核函数为高斯函数，核宽度数为10，惩罚因子设置为C=10，SMOTE，BSMOTE算法中最近邻算法参数选择为6，其他欠抽样算法保留着与少数类样本数目相同的多数类样本。代价敏感SVM算法的少数类的代价与多数类的代价比值设置为CMI/CMA=10。从表3的实验结果可以看出，针对不均衡数据集分类而言，SVM算法的Specificity性能指标多为1，Sensitivity性能指标基本为0，而其他不均衡数据分类算法在二者指标上都有明显的提高。由于G性能既考虑了多数类的样本分类性能，也考虑了少数类样本的分类性能，因此，基于代价敏感的SVM算法(SVM-WEIGHT)和自适应人工样本过抽样SVM算法(AdaSyn)在整体性能上最优。观察另一个F性能评测指标，可以看到SVM-Weight算法在该性能指标上表现较好。而同样是欠抽样算法的随机欠抽样算法RU，由于对多数类抽样的盲目性使得该算法对不均衡数据分类性能的改善不如其他算法显著。

表3 10∶1不均衡数据下，数据集F，G的性能比较Tab.3 Performance comparison of F，G in unbalanced datasets

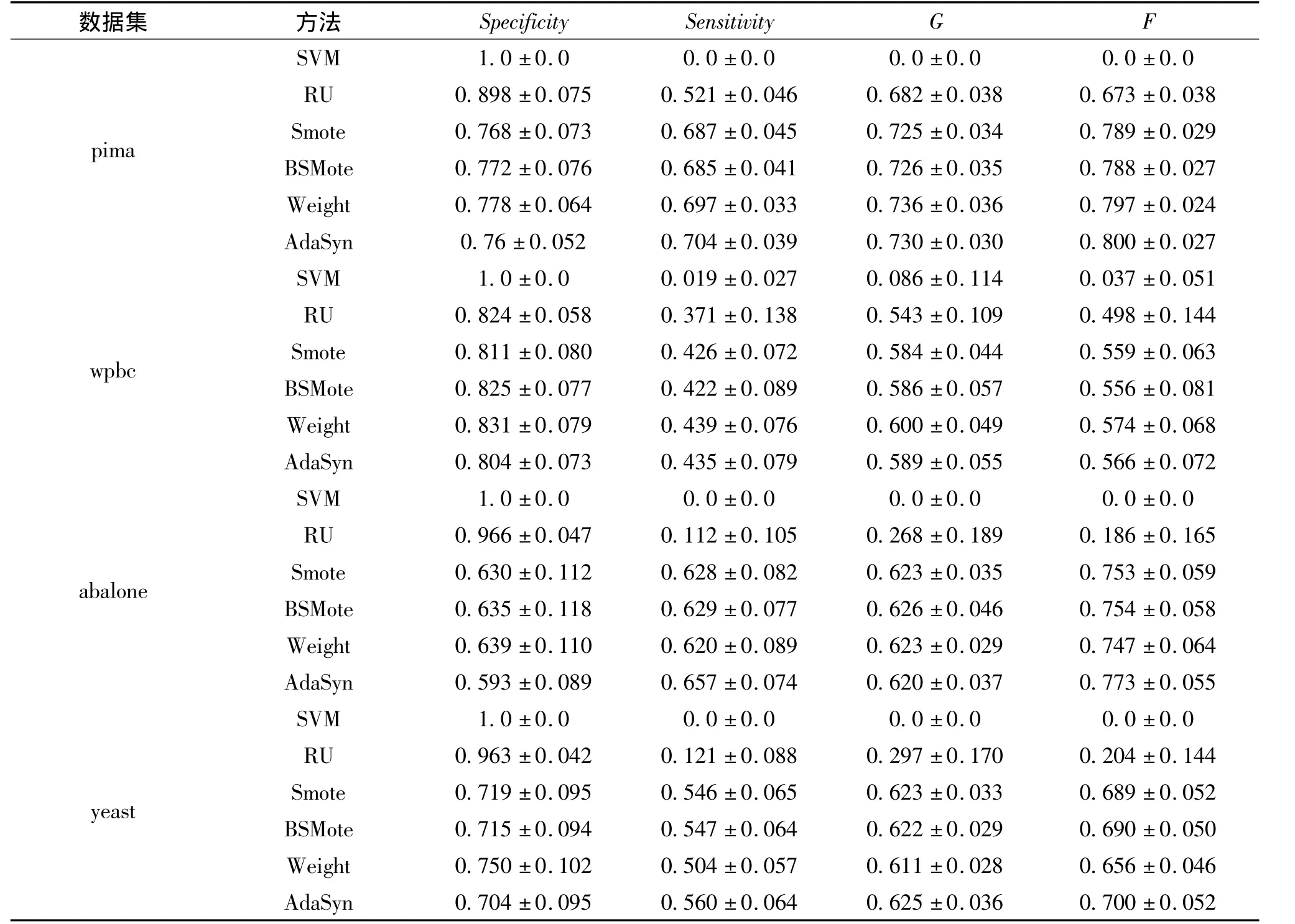
续表3

5 总结与展望

对不均衡数据分类问题，近些年，学者提出了很多解决方案，并且取得了一定的研究成果。本文首先从数据角度和算法角度对经典的解决方案进行归纳。同时，通过仿真实验比较了多种改进的不均衡分类算法在不同数据集上的分类性能。实验表明，这些改进的算法在不均衡数据分类性能上都得到不同程度的改善。结合当前不均衡数据分类的研究现状，该领域未来的发展还需解决的部分问题如下。

1)数据碎片问题。一些算法将原始的数据空间分为越来越小的一系列子空间，导致了数据碎片问题。这样就只能在各个独立的空间内归纳数据，那么每个小的子空间中所含有的少数类信息就更少了，使得一些跨类空间的数据无法被挖掘，这是影响少数类样本学习的关键。

2)归纳偏置问题。特定样本的归纳需要一个适当的偏置，这是学习的先决条件。归纳偏置对算法的性能起着关键性作用。许多算法为了避免过度拟合或是获得较好的算法性能，使用归纳偏置可能会对少数类的学习产生不利的影响。同时归纳推理系统常常将不确定的样本划分为多数类样本。因此，如何改善这一缺陷是未来学者关注的方向。

3)噪声问题。噪声会严重影响分类器的性能，对于不均衡数据分类问题，少数类样本很少，所以很难正确区分噪声和少数类样本。因此，如何抑制噪声也是目前亟待解决的关键问题。

［1］KUBAT M，HOLTE R C，MATW IN S.Machine learning for the detection of oil spills in satellite radar images［J］.Machine Learning，1998，30(223):195-215.

［2］LIU Y H，CHEN Y T.Face recognition using total margin-based adaptive fuzzy support vector machines［J］.IEEE Transactions on Neural Networks，2007:178-192.

［3］JAPKOWICZ N.Learning from Imbalanced Data Sets［C］//Proc.Am Assoc for Artificial Intelligence(AAAI)Workshop.［s.l.］:［s.n.］，2000.

［4］CHAWLA N V，JAPKOWICZ N，KOLCZ A.Workshop Learning from Imbalanced Data Sets II［C］//Proc.Int'l Conf Machine Learning.Washington DC:AAAI Press，2003.

［5］CHAWLA N V，JAPKOWICZ N，KOLCZ A.Editorial:Special Issue on Learning from Imbalanced Data Sets［J］.ACM SIGKDD Explorations Newsletter，2004，6(1):1-6.

［6］SUN Y，KAMEL M S，WANG Y.Boosting for Learning Multiple Classeswith Imbalanced ClassDistribution［C］//Proc.Int'l Conf Data Mining.［s.l.］:［s.n.］，2006:592-602.

［7］ABE N，ZADROZNY B，LANGFORD J.An Iterative Method for Multi-Class Cost-Sensitive Learning［C］//IEEE.Proc ACMSIGKDD Int'l Conf Knowledge Discovery and Data Mining.Washington:IEEE Press，2004:3-11.

［8］CHEN K，LU B L，KWOK J.Efficient Classification of Multi-Label and Imbalanced Data Using Min-Max Modular Classifiers［C］//Proc.World Congress on Computation Intelligence-Int'l Joint Conf USA:Neural Networks，2006:1770-1775.

［9］ZHOU Z H，LIU X Y.On Multi-Class Cost-Sensitive Learning［C］//Proc.Nat'l Conf Artificial Intelligence.［s.l.］:［s.n.］，2006:567-572.

［10］LIU X Y，ZHOU Z H.Training Cost-Sensitive Neural Networks with Methods Addressing the Class Imbalance Problem［J］.IEEE Trans Knowledge and Data Eng，2006，18(1):63-77.

［11］TAN C，GILBERT D，DEVILLE Y.Multi-Class Protein Fold Classification Using a New Ensemble Machine Learning Approach［J］.Genome Informatics，2003，14:206-217.

［12］HOLTE R C，ACKER L，PORTER B W.Concept Learning and the Problem of Small Disjuncts［C］//Proc.Int'l J Conf Artificial Intelligence.San Mateo，CA:Morgan Kaufman Publishers，1989:813-818.

［13］JO T，JAPKOWICZ N.Class Imbalances versus Small Disjuncts［J］.ACM SIGKDD Explorations Newsletter，2004，6(1):40-49.

［14］RAUDYS S J，JAIN A K.Small Sample Size Effects in StatisticalPattern Recognition: Recommendationsfor Practitioners［J］.IEEE Trans Pattern Analysis and Machine Intelligence，1991，13(3):252-264.

［15］WEISS G M，PROVOST F.The Effect of Class Distribution on Classifier Learning:An Empirical Study［C］//Technical Report MLTR-43，Dept of Computer Science.New Jersey:Rutgers University Press，2001.

［16］ESTABROOKS A，JO T，JAPKOWICZ N.A Multiple Resampling Method for Learning from Imbalanced Data Sets［J］.Computational Intelligence，2004，20:18-36.

［17］MIERSWA I.Controlling overfitting with multi-objective support vector machine［J］.ACM GECCO'07，2007:1830-1837.

［18］WANG B X，JAPKOWICZ N.Imbalanced Data Set Learning with Synthetic Samples［C］//Proc.IRIS Machine Learning Workshop.［s.l.］:［s.n.］，2004.

［19］CALLEJA Jorge de la，FUENTES Olac.A distance-based over-sampling method for learning from imbalanced data sets［C］//IEEE.Proceedings of the Twentieth International Florida Artificial Intelligence Research Society Conference.Florida:IEEE Press，2007:634-635.

［20］GARCÍA V，SáNCHEZ J S.On the use of surrounding neighbors for synthetic over-sampling of the minority class［C］//IEEE.Proceedings of the 8th conference on Simulation， modeling and optimization. Cantabria: IEEE Press，2008:389-394.

［21］曾志强，吴群，廖备水.一种基于核SMOTE的非平衡数据集分类方法［J］.电子学报，2009，37(11):2489-2495.ZENG Zhiqiang，WU Qun，LIAO Beishui.A Classification Method For Imbalance Data Set Based on kernel SMOTE［J］.ACTA Electronica Sinica，2009，37(11):2489-2495.

［22］李鹏，王晓龙，刘远超.一种基于混合策略的失衡数据集分类方法［J］.电子学报，2007，35(11):2161-2165.LI Peng，WANG Xiaolong，LIU Yuanchao.A Classification Method for Imbalance Data Set Based on Hybrid Strategy［J］.ACTA Electronica Sinica，2007，35(11):2161-2165.

［23］HAN H，WANG W Y，MAO B H.Borderline-SMOTE:A New Over-Sampling Method in Imbalanced Data Sets Learning［J］.Lecture Notes In Computer Science，2005，3644(1):878-887.

［24］HE H，BAI Y，GARCIA E A.Adaptive Synthetic Sampling Approach for Imbalanced Learning［C］//IEEE.Proc Int'l J Conf Neural Networks.USA:IEEE Press，2008:1322-1328.

［25］BATISTA G，PRATI R C，MONARD M C.A Study of the Behavior of Several Methods for Balancing Machine Learning Training Data［J］.ACM SIGKDD Explorations Newsletter，2004，6(1):20-29.

［26］VEERAMACHANENI S，NAGY G.Style context with second-order statistics［J］.IEEE Trans Pattern Anal Mach Intell，2005，27(1):14-22.

［27］ABE N，ZADROZNY B.Outlier detection by active learning［C］//Proceedings of the 12th ACM SIGKDD International Conf on Knowledge Discovery and Data Mining.NY，ACM Press，2006:767-772.

［28］陶新民，徐晶，童稚靖.不均衡数据下基于阴性免疫的过抽样算法［J］.控制与决策，2010，25(6):867-873.TAO Minmin，XU Jin，TONG Zhijing.Over-sampling Algorithm Based On Negative Immune In Imbalanced Data Sets Learning［J］.Control and Decision，2010，25(6):867-873.

［29］LIU X Y，WU J，ZHOU Z H.Exploratory Under Sampling for Class Imbalance Learning［C］//IEEE.Proc Int'l Conf Data Mining.［s.l.］:IEEE Press，2006:965-969.

［30］CLIFTON P，DAMMINDA A，VINCENT L.Minority Report in Fraud Detection:Classification of Skewed Data［J］.ACM SIGKDD Explorations Newsletter，2004，6(1):50-59.

［31］LAURIKKALA J.Improving identification of difficult small classes by balancing class distribution［C］//Proc.of the 8th Conference on AI in Medicine in Europe:Artificial Intelligence Medicine.London，UK:Springer-Verlag，2001:63-66.

［32］ZHANG J，MANI I.Approach to Unbalanced Data Distributions:A Case Study Involving Information Extraction［C］//Proc.Int'1 Conf Machine Learning From Imbalanced Data Sets.Washington DC:AAAI Press，2003.

［33］KUBAT M，MATWIN S.Addressing the Curse of Imbalanced Training Sets:One-Sided Selection［C］//Proc.Int'l Conf Machine Learning.San Francisco:Morgan Kaufmann，1997:179-186.

［34］YUAN J，LI J，ZHANG B.Learning concepts from large scale imbalanced data sets using support cluster machines［J］.ACM Multimedia Conference(MM)，2006:441-450.

［35］BATISTA G，PRATI R C，MONARD M C.A Study of the Behavior of Several Methods for Balancing Machine Learning Training Data［J］.ACM SIGKDD Explorations Newsletter，2004，6(1):20-29.

［36］朱明，陶新民.基于随机下采样和SMOTE的不均衡SVM 分类算法［J］.信息技术，2012:39-42.ZHU Ming，TAO Xinmin.The SVM Classifier For Unbalanced Data Based on Combination of RU-Undersample And SMOTE［J］.Information Technology，2012:39-42.

［37］陶新民，童智靖，刘玉.基于ODR和BSMOTE结合的不均衡数据SVM分类算法［J］.控制与决策，2011，26(10):1535-1541.TAO Xinmin，TONG Zhijing，LIU Yu.SVM Classifier For Unbalanced Data Based On Combination Of ODR And BSMOTE［J］.Control and Decision，2011，26(10):1535-1541.

［38］GUNETTI D，PICARDI C.Keystroke Analysis of Free tetext［J］.ACM Transaction on Information and System Security，2005，8(3):312-347.

［39］ROTH V.Kernel Fisher Discriminants For Outlier Detection［J］.Neural Computing，2006，18(4):942-960.

［40］HONG X，CHEN S，HARRIS C J.A Kernel-Based Two-Class Classifier For Imbalanced Datasets［J］.IEEE Transactions on Neural Networks，2007，18(1):28-41.

［41］陈斌，冯爱民.基于单簇类聚类的数据描述［J］.计算机学报，2007，30(8):1325-1332.CHEN Bin，FENG Aimin.One-Clustering Based Data Description［J］.Chinese Journal of Computers，2007，30(8):1325-1332.

［42］WANG D F，YEUNG D S.Structured one-class classification［J］.IEEE Trans on Systems and Cybernetics，2006，36(6):1283-1295.

［43］BREIMAN L.Bagging Predictions［J］.Machine Learning，1996，24(2):123-140.

［44］BREIMAN L.Random forests［J］.Journal Machine Learning，2001，45(1):5-32.

［45］张晓龙，任芳.支持向量机与AdaBoost的结合算法研究［J］.计算机应用研究，2009，26(1):77-79.ZHANG Xiaolong，REN Fang.Study On Combinability of SVM And Adaboost Algorithm［J］.Application Research of Computers，2009，26(1):77-79.

［46］GUO H，VIKTOR H L.Learning from Imbalanced Data Sets with Boosting and Data Generation:The DataBoost IM Approach［J］.ACM SIGKDD Explorations Newsletter，2004，6(1):30-39.

［47］GUO H，VIKTOR H L.Boosting with Data Generation:Improving the Classification of Hard to Learn Examples［C］//IEEE.Proc Int'l Conf.Innovations Applied Artificial Intelligence.USA:IEEE Press，2004:1082-1091.

［48］CHAWLA N V，LAZAREVIC A，HALL L O，et al.SMOTEBoost:Improving Prediction of the Minority Class in Boosting［C］//Proc.Seventh European Conf.Principles and Practice of Knowledge Discovery in Databases.Cavtat-Dubrovnik，Croatia:［s.n.］，2003:107-119.

［49］MEASE D，WYNER A J，BUJA A.Boosted Classification Trees and Class Probability/Quantile Estimation［J］.Machine Learning Research，2007，8:409-439.

［50］李想，李涛.基于核函数的Adaboost分类算法研究［J］.电脑知识与技术，2011，7(28):6970-6979.LI Xiang，LI Tao.Classification Algorithm of Kernelbased In Adaboost［J］.Computer Knowledge and Technology，2011，7(28):6970-6979.

［51］顾磊，吴慧中，肖亮.一种基于核的模糊多球分类算法及其集成［J］.计算机工程与应用，2007，43(27):10-12.GU Lei，WU Huizhong，XIAO Liang.Kernel-based Fuzzy Multiple Spheres Classification Algorithm And Its Ensemble［J］.Computer Engineering and Applications，2007，43(27):10-12.

［52］陶新民，刘福荣，杜宝祥.不均衡数据SVM分类算法及其应用［M］.哈尔滨:黑龙江科技技术出版社，2011:223-257.TAO Xinmin，LIU Furong，DU Baoxiang.Unbalanced Data SVM Classification Algorithm And Application［M］.Harbin:Heilongjiang Science and Technology Press，2011:223-257.

［53］ZHOU Z H，LIU X Y.The Influence of Class Imbalance on Cost-Sensitive Learning:An Empirical Study［C］//IEEE.In Proceedings of the sixth IEEE International Conference on Data Mining(ICDM'06).Hong Kong，China:IEEE Press，2006:970-974.

［54］WU J，BRUBAKER S C，MULLIN M D，et al.Fast asymmetric learning for cascade face detection［J］.IEEE Transactions on Pattern Analysis and Machine Intelligence，2008，30(3):369-382.

［55］陶新民，刘福荣，童智靖，等.不均衡数据下基于SVM的故障检测新算法［J］.振动与冲击，2010，29(12):8-12.TAO Xinmin，LIU Furong，TONG Zhijing，et al.A New Algorithm Of Fault Detection Based On SVM In Unbalanced Data［J］.Journal of Vibration and Shock，2010，29(12):8-12.

［56］WU G，KBA Chang E Y.kernel boundary alignment considering imbalanced data distribution［J］.IEEE Trans on Knowledge and Data Engineering，2005，17(6):786-795.

［57］李俊林，符红光.改进的基于核密度估计的数据分类算法［J］.控制与决策，2010，25(4):507-513.LI Junlin，FU Hongguang.Improved KDE-based Data Classification Algorithm［J］.Control and Decision，2010，25(4):507-513.

［58］ZHENG Z，WU X，SRIHARI R.Feature selection for text categorization on imbalanced data［J］.SIGKDD Explorations，2004，6(1):80-89.

［59］KINGSBURY N，TAY D B H，PALANISWAMI M.Multi-scale kernel methods for classification［C］//IEEE.Proceedings of the IEEE Workshop on Machine Learning for Signal Processing.Washington D.C:USA:IEEE Press，2005，43-48.