相位偏差估计及其在PPP模糊度固定中的应用分析*

赵兴旺 张翠英

(安徽理工大学测绘学院，淮南 232001)

相位偏差估计及其在PPP模糊度固定中的应用分析*

赵兴旺 张翠英

(安徽理工大学测绘学院，淮南 232001)

在分析相位偏差与精密单点定位模型在模糊度解算中内在关系的基础上，依据方向数据统计理论建立了相位偏差估计模型，设计了精密单点定位模糊度固定方案，解决了精密单点定位单差模糊度固定的问题。实验结果表明，在相位偏差改正后，精密单点定位模糊度固定解的收敛速度较浮点解提高了3/4左右、模糊度固定的Ratio因子较未改正提高了3倍、定位精度也得到明显提高。

精密单点定位;相位偏差;模糊度;固定解;Ratio值

1 引言

快速有效地固定模糊度是实现固定解精密单点定位的关键所在。然而非零相位偏差和硬件延迟的存在致使非差和单差观测值模糊度不再具有整周性质，难以准确固定。针对这一问题的研究形成了两种不同的处理策略:一种是从整数与小数分离角度进行考虑的分离法［1－6］;另一种是从卫星钟差估计角度考虑的分解法［7，8］。这两种算法均借助区域或全球范围的GNSS参考站网络估计卫星相位偏差，前者直接采用卫星的精密轨道和钟差信息，但难以准确获得相位偏差小数估值，后者需要对卫星钟差进行参数估计，较为复杂。因此，本文在第一种方法的基础上以星间差分相位偏差为研究对象，采用方向数据统计理论对相位偏差估计方法进一步研究，并考虑精密单点定位(PPP，Precise Point Positioning)无电离层组合模糊度的特点，优化设计PPP模糊度固定方法。最后，对算法以及PPP固定解的有效性进行了分析。

2 相位偏差估计

在GPS导航定位中，伪距和载波相位观测量表达式为［9］:

式中，dr为接收机端的硬件码延迟，ds为卫星端的硬件码延迟，δr为接收机端的载波相位硬件延迟，δs为卫星端载波相位硬件延迟，φr(t0)为零时刻接收机本地信号的初始相位，φs(t0)为零时刻卫星信号的初始相位，其余参数见文献［9］。

由于初始相位和载波相位硬件延迟不可分离，且均对载波相位模糊度产生直接影响，因此本文将初始相位和载波相位有关的硬件延迟统称为相位偏差。此时，对式(1)在卫星i和j之间求一次差消除接收机端相位偏差，并组合成无电离层观测值为

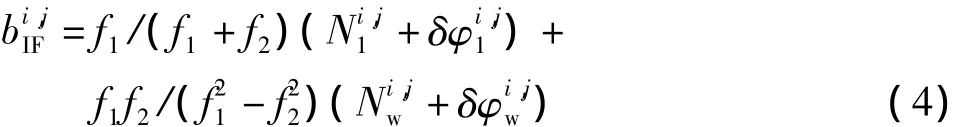
式中，、δ分别为 L1 模糊度与相应的卫星端相位偏差，、δ分别为宽巷模糊度与相应的卫星端相位偏差。

由于相位偏差与整周模糊度线性相关，参数估计时往往并入整周模糊度参数。但相位偏差整数部分对模糊度的整周性质并不产生影响，可以与模糊度并作一项处理，而剩余小数部分是破坏模糊度整周性质的主要原因。因此，为了得到PPP模糊度固定解，必须对这部分相位偏差进行改正以还原模糊度的整周特性。

根据相位偏差的形成机理可知，对于不同测站的星间差分相位偏差应具有近似相等的偏差小数部分。因此，从整数与小数分离的角度采用星间差分模式对卫星端相位偏差小数部分进行估计。主要分为三步:1)按照标准PPP模型，以跟踪站精确坐标为约束条件逆向求取各站点的PPP模糊度实数解;2)采用M-W组合模型对跟踪网多个测站数据进行联合解算，得到宽巷模糊度的估计值，确定单差宽巷相位偏差小数估值与模糊度固定解;3)将固定的宽巷模糊度与估计得到的无电离层模糊度进行组合，得到L1模糊度的估计值，分离出L1相位偏差小数。由此得到近似适合该区域的宽巷与L1观测值的相位偏差小数估值，用于还原单差模糊度的整数特性，实现PPP固定解。

2.1 相位偏差计算

由文献［10，11］可知，相位偏差小数服从方向数据统计中的Von Mises分布，因此将包含相位偏差的整周模糊度参数作相应的方向数据变换，采用方向数据理论［12］计算偏差小数:

式中，n为参与计算的模糊度个数。

经过式(5)中三角函数作用后，整周模糊度与相位偏差整数部分均被移去，仅剩下相位偏差小数部分，进而得到相位偏差小数估值δfrac:

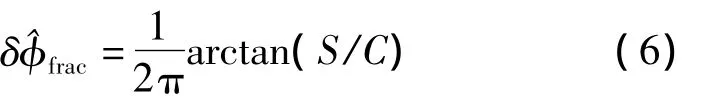
对于特定的一组卫星对，由某一测站估计得到的所有历元的单差相位偏差求均值可以确定为该观测站在该观测时段内的相位偏差值，进一步综合分析多个观测站的相位偏差小数估值确定星间差分的相位偏差改正值。

2.2 宽巷模糊度相位偏差解算

采用双频P码M-W法固定宽巷模糊度。由式(1)、(2)分别组成的伪距窄巷和载波相位宽巷观测值为［1］:

将两式相减，对卫星i和卫星j形成星间一次差，消除接收机相位偏差影响。则宽巷模糊度为

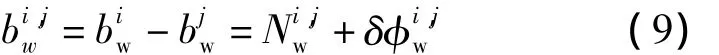
式中，为单差宽巷整周模糊度相位偏差，δφ为宽巷相位偏差，由整数和小数部分组成，其中小数部分将直接影响模糊度的准确固定。本文通过式(9)对测试网内多个基准站的每一弧段进行计算，确定含有相位偏差δφi，jw在内的宽巷模糊度参数的综合估值。最后，依据式(5)和式(6)分离出δ，表达式为

对宽巷组合模糊度进行相位偏差小数改正后，采用取整法确定其固定解，

式中，int(·)表示取整。

2.3 L1模糊度相位偏差解算

由式(4)知，L1相位模糊度的浮点解可由无电离层组合模糊度浮点解和宽巷整周模糊度进行组合确定［1］，

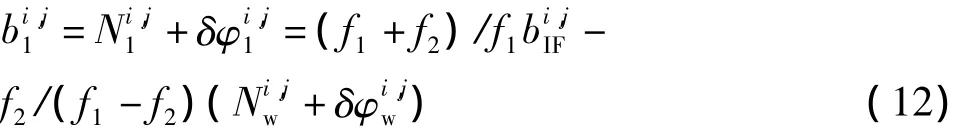
进一步变换，得

式中，为单差 L1 载波相位整周模糊度，δ为单差L1相位偏差，b^iw，j为宽巷组合模糊度整数解，为单差无电离层组合模糊度的浮点解。

为了便于估计，研究过程中将式(13)中L1相位偏差和宽巷相位偏差的影响并为一项作为L1相位偏差对L1整周模糊度的综合影响，并令=)，便得到 L1 相位偏差的最终估计形式为

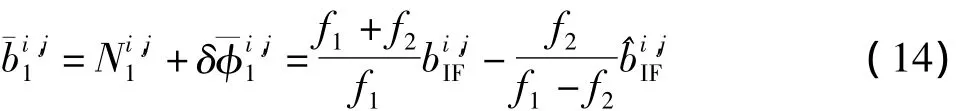
3 单差PPP模糊度固定方案

精密单点定位固定解技术是基于还原模糊度整周特性基础上实现的，除了使用精密卫星轨道和钟差外还需要卫星端相位偏差改正信息，它的估计质量与分布特性对终端用户实现PPP整数解至关重要。因此，为了尽量避免码偏差等对相位偏差估计的影响，用户端采用的偏差改正模型应与相位偏差估计模型保持一致。

首先将载波相位单差宽巷模糊度浮点解bi，jw固定为整数，

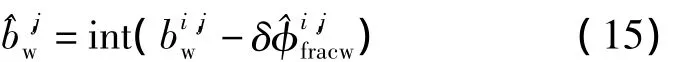
式中为固定后的宽巷组合观测值的模糊度，包含单差宽巷模糊度和相位偏差整数部分，int(·)表示取整。由于估计时采用伪距观测值，因此需要通过一段时间的平滑，这个时间依赖于伪距测量噪声、多路径效应以及大气延迟的影响。如果成功地将固定为整数，则可以根据估计出的L1相位偏差小数通过

恢复L1模糊度的整周性质。式中b'i，j1为改正后得到的L1观测值的模糊度浮点解，包含模糊度Ni，j1和相位偏差整数部分。

根据协方差传播率，得到L1模糊度浮点解的近似协方差为

经相位偏差改正后的L1模糊度已恢复整周特性，于是采用LAMBDA整周模糊度搜索方法将其固定，其中LAMBDA算法的输入量为浮点解和协方差阵为 Db1'i，j。将固定后的宽巷模糊度和L1模糊度进一步组合成无电离层组合的模糊度为

式中为分步逐一固定后的无电离层模糊度，用它进行PPP定位以达到利用模糊度整周性约束定位解算的目的，能够有效提高定位精度和收敛速度。

4 PPP单差固定解分析

为验证相位偏差对模糊度的影响以及PPP固定方法的正确性，以IGS连续运行参考站观测数据为实验数据，从精密单点定位固定解的收敛速度、定位精度和模糊度固定可靠性等方面进行测试分析。

测试网络由国际GNSS服务跟踪网络中ARTU、BJFS、WUHN、SHAO、PETS等18个GPS跟踪站组成(图 1)。其中，ARTU、BJFS、MOBN、SHAO、PETS、WUHN六个站用于测试PPP固定解性能，其余用于确定相位偏差改正信息。测试数据选自2010年第102天08:00—10:30的观测数据，采样率均为30 s，分别对传统PPP解算、相位偏差改正后固定以及未改正直接固定三种解算方式进行对比分析。

图1 站点分布Fig.1 Stations distribution

为了尽可能提高模糊度正确固定的概率和可靠性，在相位偏差改正与未改正PPP固定解测试中，均采用100个历元的观测数据来初始化整周模糊度，即由式(16)、(17)确定L1载波相位单差模糊度浮点解及协方差阵，进而由LAMBDA算法将L1模糊度固定，结合宽巷单差模糊度固定解由式(18)得到无电离层模糊度整数解。

但目前，权威机构并未对相位偏差改正信息进行有效发布，并且难以得到准确的单差模糊度值进行比对。因此，本文将以PPP定位解的精度为参考来判断模糊度是否成功固定。表1给出了ARTU站L1相位偏差小数估值，以及改正前后模糊度整周固定解，图2给出了三种解算方式的定位误差曲线。

表1 ARTU L1单差模糊度整数解(参考卫星为PRN19)Tab.1 Ambiguity integer solution of Singlesingle-difference L1 for ARTU(With with respect to PRN19)

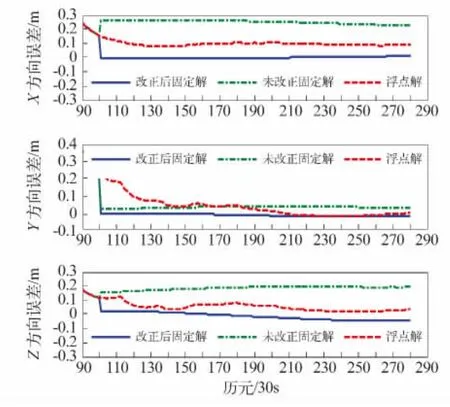
图2 ARTU固定解与浮点解坐标定位误差Fig.2 Positioning errors of ambiguity fixing solution and floating solution for ARTU

从图2明显看出，改正后固定解的三个方向分量在模糊度初始化后快速达到厘米级，定位精度较其他两种方式明显改善。由统计信息知，此时三个方向分量固定解的误差均值为(－0.004 m，－0.018 m，－0.011 m)，且离散度小，均方根误差为(0.004 m，0.007 m，0.025 m)。表明经相位偏差改正后的L1单差模糊度整数值为正确值，没有进行偏差改正得到的整数解精度较低，在X方向与Z方向仅为分米级。因此未进行相位偏差改正直接由LAMBDA方法搜索得到的模糊度值为错误值，此时模糊度固定失败。这一现象表明相位偏差的存在会导致模糊度的错误固定。

图3～6给出了其他测试点L1单差模糊度固定情况和定位结果。表2给出了PPP浮点解与偏差改正后固定解两种方式定位精度达到厘米级所需的历元个数信息。对于传统浮点解收敛到厘米级需要时间较长，甚至三个测站出现未收敛的现象。而改正后固定解所需时间较短，但部分测站仍需经过少许历元的收敛，分析原因主要为单差模式较双差模式更易受残余误差影响，并且模糊度固定后仍将对流层作为待估参数所致。但从历元个数来看，达到厘米级精度较浮点解收敛速度提高了3/4左右。图3为L1模糊度固定的Ratio值。相比于未改正而直接采用LAMBDA固定时，不难看出引入相位偏差改正后，L1单差模糊度固定的Ratio因子平均提高了3倍。因此，相位偏差改正后提高了模糊度固定的可靠性。

图3 模糊度固定Ratio值Fig.3 Ratio values of ambiguity fixing

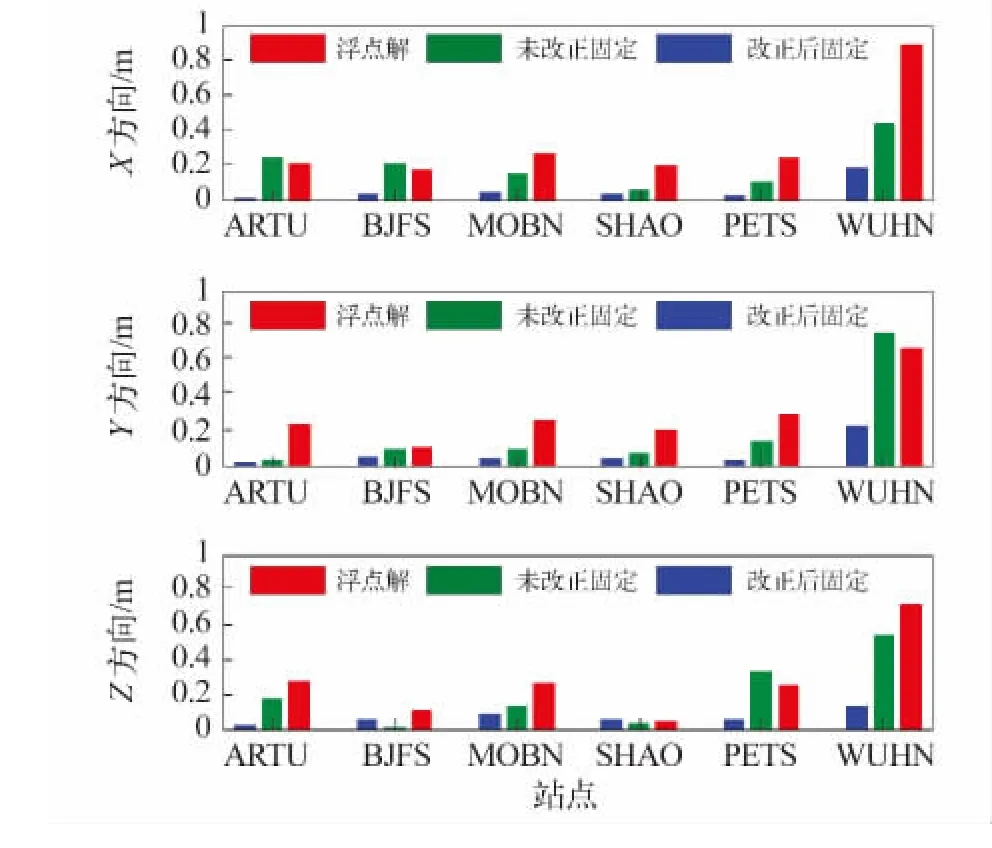
图4 PPP均方根误差Fig.4 Root mean square errors of PPP

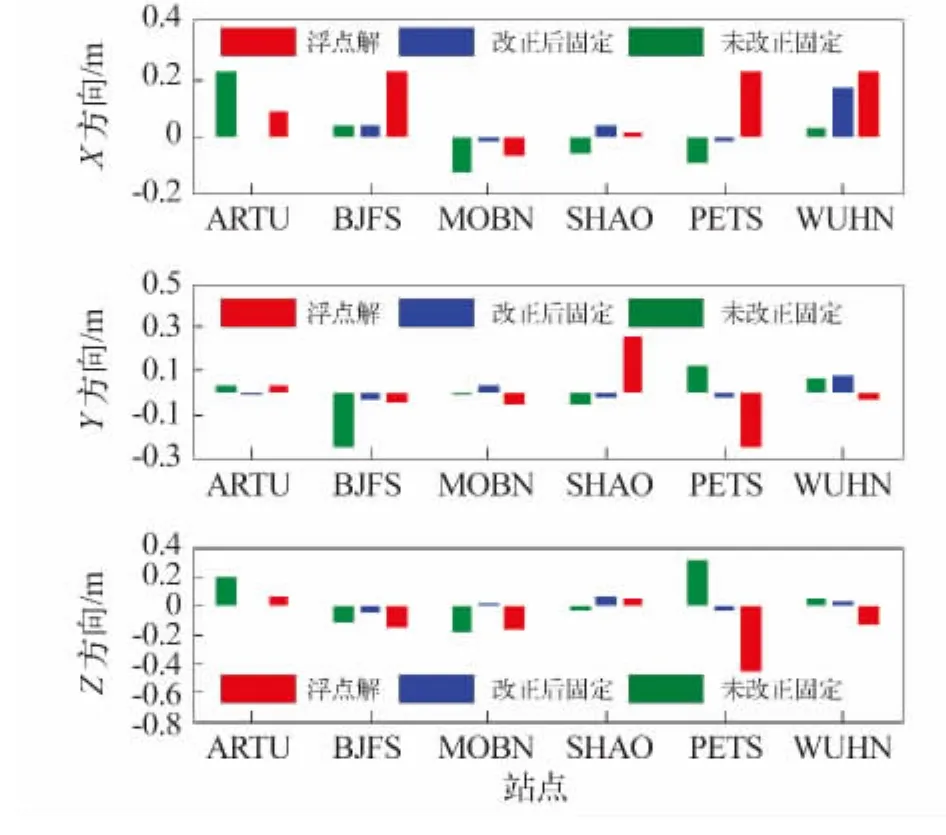
图5 PPP误差均值Fig.5 Average errors of PPP

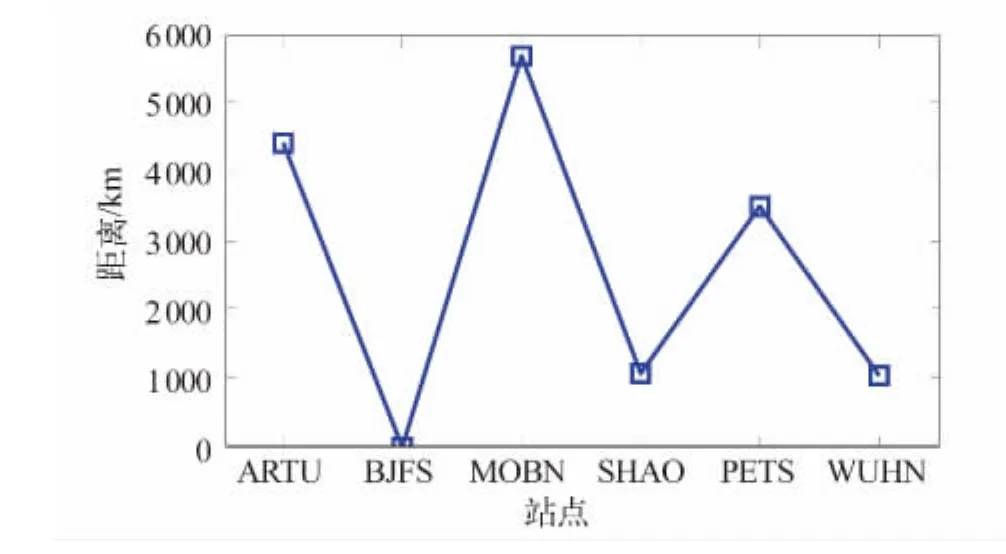
图6 与BJFS站间距离Fig.6 Distances between BJFS and other stations

图4为PPP三种解算方式位置解的均方根误差，图5为误差均值。由图4和图5可知，相对于浮点解，测试站点位精度均有显著提高，其中SHAO、PETS等站点，由于PPP模块的不完善以及残余误差的影响，PPP浮点解没有达到厘米级，当经过相位偏差改正后的固定解能够达到厘米级，但需要十几个历元的收敛时间(表2)。对于相位偏差改正的有效性，SHAO站点从定位精度方面表现的并不突出，但结合图3中模糊度固定Ratio值可发现未改正固定解可信度低。另外，由于L1单差相位偏差空间分布一致性较差，采用求平均方向的方式确定的L1单差相位偏差可能会导致部分卫星的相位偏差与实际值不符。如图4中测站WUHN的定位结果出现了异常情况，从定位结果中看不出引入相位偏差改正对PPP位置解的精度和收敛速度有明显提高，而未进行偏差改正固定的Y方向出现严重发散现象;结合表2可以看出两种方案固定的Ratio因子小于检验阈值，所固定的模糊度可信度低。因此，认为相位偏差改正值对该点失效，所固定的模糊度不可接受。为了避免局部区域内出现改正无效的现象，仍需要对L1相位偏差估值的探测作进一步深入研究。

表2 厘米级PPP定位收敛时间表Tab.2 Convergence time of the centimeter-level PPP positioning

另外，图6给出了各站相对于BJFS站的站间距信息。结合图4和图5的定位结果可以看出，除WUHN站外相位偏差均能有效得到改正，这表明相位偏差改正信息的有效性并不受距离的限制，通过少数跟踪站网络估计出的相位偏差改正信息可用于广域范围内PPP用户实现厘米级精密单点定位。

5 结论

在传统PPP模型中，忽略了GPS观测值中包含的相位偏差是导致精密单点定位估值均为模糊度浮点解的关键因素。根据本文给出的相位偏差改正方法，设计了PPP模糊度固定方案。实验结果表明，采用估计得到的相位偏差对GPS观测值进行改正能够提高PPP模糊度固定的收敛速度和可靠性，较快地实现了PPP模糊度固定解。整体上表明该方法可用于广域范围内PPP用户快速实现厘米级精密单点定位。但由于L1单差相位偏差空间分布一致性较差及PPP模型不完善等因素，可能会导致部分卫星的相位偏差估值与实际值不符，出现个别站点相位偏差改正无效的现象(如WUHN站点)，这一问题还有待进一步研究。

1 Ge M，et al.Resolution of GPS carrier-phase ambiguities in Precise Point Positioning(PPP)with daily observations［J］.Journal of Geodesy，2008，82:389－399.

2 Li X，Zhang X and Ge M.Regional reference network augmented precise point positioning for instantaneous ambiguity resolution［J］.Journal of Geodesy，2011，85(3):151 －158.

3 张宝成，等.精密单点定位整周模糊度快速固定［J］.地球物理学报，2012，55(7):2 203－2 211.(Zhang Baocheng，et al.Rapid integer ambiguity-fixing in precise point positioning［J］.Chinese Journal of Geophysice，2012，55(7):2 203－2 211)

4 Gao Y and Chen K.Performance analysis of precise point positioning using real-time orbit and clock products［J］.Journal of Global Positioning System，2004，3(2):95－100.

5 张小红，李星星.非差模糊度整数固定解PPP新方法及实验［J］.武汉大学学报(信息科学版)，2010，35(6):657 －660.(Zhang Xiaohong and Li Xingxing.A new method for zero differenced interger ambiguity resolution and its application to PPP［J］.Geomatics and Information Science of Wuhan University，2010，35(6):657－660)

6 Geng J，Meng X and Dodson A.Integer ambiguity resolution in precise point positioning:method comparison［J］.Journal of Geodesy，2010，84(9):569－581.

7 Leandro R and Santos M.Wide area based precise point positioning［A］.Proceedings of ION GNSS 2006［C］.Fort Worth，TX，2006:2 272－2 278.

8 Collins P.Isolating and estimating undifferenced GPS integer ambiguities［A］.Proceedings of ION NTM-2008［C］.San Diego，CA，2008:720－732.

9 Teunissen P J G and Kleusberg A.GPS for geodesy［J］.Lecture Notes in Earth Sciences，1996，60:175 －217.

10 Keshin M.Directional statistics of satellite-satellite singledifference widelane phase biases［J］.Article Satellites，2004，39(4):305 －324.

11 Cai J，Grafarend E and Hu C.The statistical property of the GNSS carrier phase observations and its effects on the hypothesis testing of the related estimators［A］.Proceedings of ION GNSS 2007［C］.Fort Worth，TX，USA，2007:331－338.

12 Jammalamadaka S R and SenGupta A.Topics in circular statistics［M］.Malaysia:World Scientific Publishing，2001.

PHASE BIAS ESTIMATION AND ITS APPLICATION IN PPP AMBIGUITY FIXING

Zhao Xingwang and Zhang Cuiying
(School of Geodesy and Geomatics，Anhui University of Science＆Technology，Huainan232001)

According to the relationship between the phase biases and precise point positioning(PPP)model in ambiguity resolution，the estimation model for phase biases is derived based on the directional statisticsnd，and the ambiguity fixing scheme for PPP is designed which can solve the problem of ambiguity fixing for PPP.The results show that，based on phase biases correction，the convergence speed of PPP ambiguity fixed solution is improved by 3/4 compared with floating solution，the Ratio value is improved by three times，and positioning accuracy is also obviously improved.

Precise Point Positioning(PPP);phase biases;ambiguity;fixed solution;Ratio value

P228.1

A

1671-5942(2013)05-0124-06

2013-03-18

安徽省国土资源科技项目(2011－K－22);淮南市科技计划项目(2013A4021);安徽理工大学硕博基金

赵兴旺，男，博士，讲师，研究方向为GPS精密定位方法与应用.E－mail:xwzhao2008@126.com