基于改进遗传算法的含分布式电源的配电网故障定位

王进强，陈少华

(1.广东电网公司 茂名信宜供电局，广东 信宜 525300;2.广东工业大学 自动化学院，广东 广州 510006)

0 引言

分布式发电因具有能耗低、清洁环保、供电灵活等优点而逐渐被重视并在近几年得到迅速发展和应用。随着大量的分布式电源接入配电网，配电网由传统的单电源辐射型网络逐步发展成复杂的多电源网络。已有的故障定位方法受到了影响，甚至出现误判。解决多电源的配电网故障定位的问题，对提高配电网供电可靠性以及促进分布式发电的发展均具有重要的意义。

目前解决故障定位的方法主要有矩阵算法[1～4]、神经网络算法[5]、专家系统[6]、遗传算法[7～9]等。矩阵算法较直观且计算速度快，但对故障上传的信息要求比较准确，其容错性较差。神经网络具有较强的自学习能力、非线性映射能力和容错能力;国内外均已有不少文献应用神经网络进行电力系统的故障检测和故障定位;但神经网络存在训练结果不稳定，容易陷入局部最优解，且过分依赖学习样本以及泛化能力不够强的缺陷。专家系统通过将获取的故障信息与知识库中的记录进行比较来确定故障位置，定位准确率较高;但是专家系统中的专家知识库的建立与维护是一件烦琐和艰巨的工作，往往由于知识库的维护不到位使得专家系统在适应网络结构变化方面不尽人意。遗传算法是根据人类遗传机理而提出的一种全局优化算法，能从全局优化的角度出发解决故障诊断问题，能够得出全局最优解，具有较高的容错性。

本文对已有的遗传算法进行改进，使得改进后的遗传算法能适用于含分布式电源的配电网故障定位，具有一定的实用性。

1 基于改进遗传算法的故障定位基本原理

1.1 编码问题

配电网某一段线路发生故障时，FTU监测点将通过SCADA控制中心上传开关的故障过流情况。文献[7]中规定，当开关的FTU监测点检测到故障过流方向与所定义的正方向相同时，开关编码为1，其他情况编码为0。这样定义无法很好地解释含多个电源的配电网实际的潮流方向。本文对开关进行重新编码。定义开关的正方向是由开关的上游电源指向下游电源。

对于某一个开关，上游电源定义为与该开关距离最近的电源，网络中其他电源则为下游电源;当出现距离相等的电源时，可以任意取其中一个电源作为该开关的上游电源。已有的文献对配电网络正方向的定义均是假设网络只有其中一个电源供电时的潮流方向为该网络的正方向，全网络就只有一个正方向。本文定义某个开关的正方向是从上游电源指向下游电源，其实这个定义与传统的定义相类似:就是对某一个开关而言，假定全网络只有该开关的上游电源供电时的潮流方向为该开关的正方向，这样的定义使得该网络中每一个开关只有一个确定的正方向，该正方向对网络而言无意义，只是针对某一个开关。根据开关的上下游电源的定义，对特定的配电网络、每个开关均有其唯一的正方向，也有唯一的上下游元件。

当FTU监测点检测到故障过流方向与该开关所定义的正方向同向时，开关的状态值Ij为“1”;方向相反时，Ij的值为“-1”;没有故障过电流时，Ij的值则为“0”。对开关的故障电流状态使用“-1”编码是考虑到接入分布式电源的配电网与单电源辐射状的馈线结构不同，在分布式电源接入的支路上的开关流过的故障电流可能会与接入前的方向相反;因此增加“-1”编码能更好反映这种含DG的配电网络。两个开关之间的线路的状态依然还是定义故障状态为“1”，非故障状态为“0”。

图1为含两个DG的配电网结构简图。开关S1，S2和S3的上游电源可以取为主电源S，下游电源为DG1和DG2;其他开关可以类推。以开关S4为例，其正方向就规定为由上游电源DG1指向下游电源S和DG2;在馈线c上发生故障K1时，流过开关S4的故障过电流与假定的正方向相同，开关的状态值Ij就为“1”;在馈线d处发生故障K2时，开关S4流过由主电源S和分布式电源DG2共同提供的电流，其方向与假定的正方向相反，开关的状态值Ij就为“-1”;当网络无故障发生时，开关的状态值Ij就为“0”。当发生故障 K1时，故障线路c为故障状态，对应的编码为“1”，其他非故障线路对应的编码为“0”。

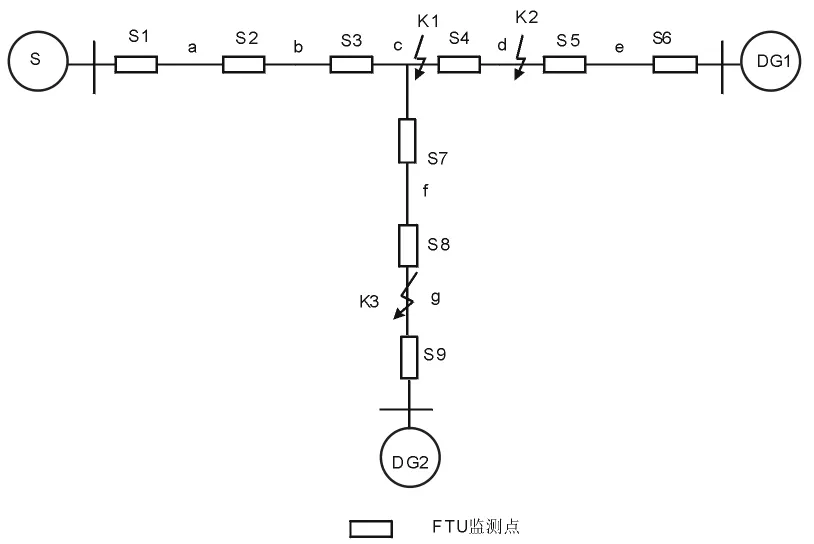
图1 含DG的配电网简化结构Fig.1 The simplified structure of distribution network with DG

1.2 建立改进的开关函数

含分布式电源的配电网中某一处发生故障时，配电网自动化系统得到的故障信息是由监控终端设备FTU上传到SCADA控制中心的各个开关的故障电流越限信号。因此，要利用遗传算法分析各个开关的故障电流越限信号来确定具体的故障线路，就必须建立一个从故障线路的状态到开关的故障电流越限情况的转换。这就是开关函数，它反映了各段线路与开关之间的关联关系。

对于单电源供电的网络，一个开关的过流与否只与开关后面的线路是否发生故障有关;但是一个开关可能由多个电源供电时，那么开关的过流就与各个电源都有关了。因此，新的开关函数也应该能适应多电源的网络，本文定义新的开关函数为

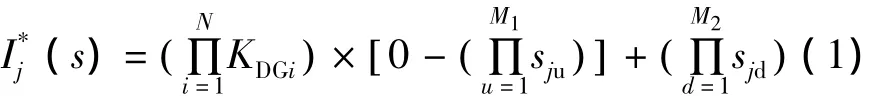
1.3 适应度函数的构造

适应度函数也叫评价函数，它的构造是遗传算法是否能够成功实现故障定位的关键。一直以来，适应度函数的构造是遗传算法在配电网故障定位的应用所遇到的瓶颈。适应度函数能否充分表达所要求解问题的本质，对遗传算法能否得到最优解有着决定性的影响。适应度函数构造得越合理，则最终解与最优解就越接近，甚至最终解就是最优解;反之就很难保证最终解接近最优解。基于遗传算法的配电网故障定位，不同的适应度函数在应用时会得出不同的判断并且具有不同的容错能力。利用遗传算法对配电网络进行故障定位，就是在一个由所有可能的故障线路组成的解空间中，找到这个故障线路，这个故障线路最能解释由FTU上传到SCADA控制中心的各个开关的故障电流越限信号。根据这个思想构造的适应度函数如式 (2)所示。

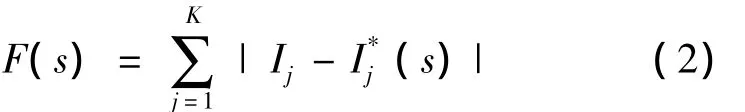
式中:K为开关的总数。s为馈线的状态向量，它由各段馈线的状态组成，当某段馈线为故障状态时用元素“1”表示，正常时用“0”表示。Ij是第j个开关的故障电流越限信号，是FTU反馈到SCADA控制中心的各个开关的实际状态，对适应度函数而言是一个已知量，当过流信息与开关的正方向相同时为“1”，相反时为“-1”，没有过流信息则为“0”。I*j(s)为开关函数，是开关j的期望状态，可由式 (1)计算出。当开关的期望状态I*j(s)与开关的实际状态Ij一样时，适应度函数F(s)就取得最小值。因此，求解适应度函数的过程就是在解空间中搜索最优解的过程，也就是寻找能使式 (2)最小的解群的过程。在这个解 (数字串或染色体)中的值对应的馈线段即为实际的故障线段。

实际上，式 (2)的适应度函数是存在缺陷的，自故障点至电源点这一条线路上的各段线路均有可能被误判[8]。本文在式 (2)的右边增加一个附加项，改进后的适应度函数如式 (3)所示。

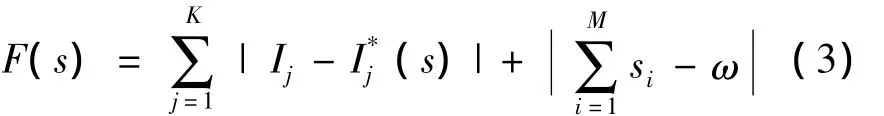
根据故障诊断理论中著名的“最小集”概念，即在可能的故障诊断结果中选取故障线路数目最小的解，在原来的适应度函数上增以防止误判，其所有线路的故障状态之和。本文在防止误判的同时，增加了ω来防止漏判。

如图2，在某馈线L上的a处发生故障K时，有可能出现无故障的漏判，因为此时I1为1，I2，I3和I4都为0。有两种情况可以使得式 (3)的目标函数取得最小值:一是假设 a故障，那么式(3)右边第一项为0，第二项为1，适应度值为1;二是假设a正常，那么式 (3)右边第一项为1，第二项为0，适应度值也为1。因此如果求得最优解的是第二种情况，则漏判故障。式 (3)中的ω只要取一个小于1的正数就可以使得第一种情况的适应度值是一个小于1的正数，小于第二种情况的适应度值，从而防止漏判故障。综上所述，增加ω项可以防止一个最优解对应多个解空间，防止漏判故障的现象，ω的取值应该大于0而小于1。

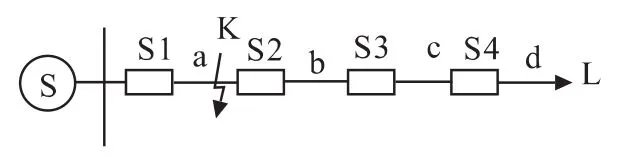
图2 馈线L上发生故障KFig.2 Fault K on the feeder L

改进后的适应度函数防止了误判和漏判的现象，同时在容错性能上也有一定的提高。遗传算法的应用依赖于FTU反馈的故障电流越限信号。由于FTU大多安装在户外，有诸多不利的因素使得故障信息受干扰或丢失。在FTU反馈回SCADA控制中心的信号因某种原因发生畸变时，例如，开关值Ij由原来“1”变为“0”或者“-1”，式(2)的适应度函数很可能会发生误判的现象。以图2为例，在馈线L上发生故障K，FTU反馈回SCADA控制中心应该是开关S1有正方向的故障电流越限信号，I1为“1”，其他开关均无电流越限，即I2，I3和I4都为“0”。如果因为某种原因使得I4的信号变为“1”，那么式 (2)的适应度函数求得最优解就可能包括在馈线段d上也发生故障。而式 (3)所示的适应度函数，在馈线段a，d上同时发生故障时的适应度值比仅在a处发生故障时要大，因此不会判断在d上发生故障。通过以上分析，改进后的适应度函数增强了遗传算法的容错性。

1.4 遗传操作

遗传操作包括选择、交叉和变异。通过选择、交叉以及变异可保证遗传算法快速而准确地收敛于全局最优解。

2 算例仿真

2.1 单重故障

以图1为例进行计算。两个分布式电源默认均接入配电网络，并假设在线路c发生故障K1。由式 (1)可计算各开关S1的开关函数如式 (4)。

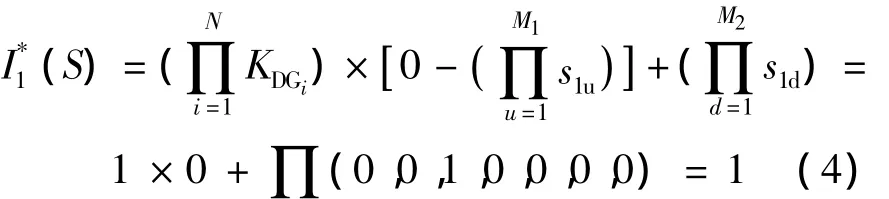
同理可计算其他开关的开关函数值均为1。

发生故障K1时，流过各个开关的故障电流的方向均与开关自身的正方向相同，因此，由FTU上传的各个开关的故障电流状态值Ij均为“1”。取ω为0.5，由式 (3)计算适应度函数值如式(5)所示。

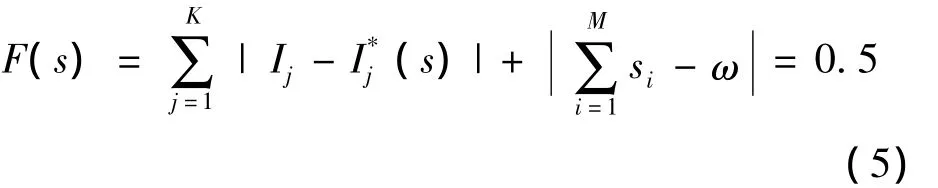
根据已知的故障电流越限信息，即各开关的Ij值，借助遗传算法工具箱对故障K1进行仿真分析，结果如图3所示。

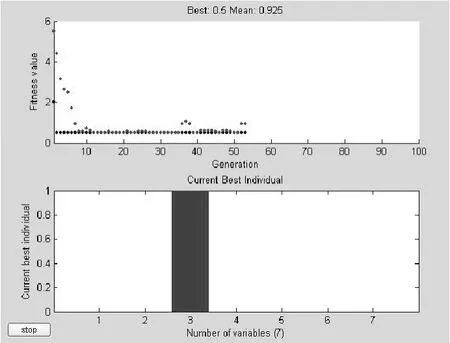
图3 故障K1的仿真结果Fig.3 Simulation results of fault K1

由图3可知，当种群经过53代的遗传操作时取得了最小的适应度值0.5，最优个体为3，而个体3所对应的线路为c。因此故障线路即为c。这与理论计算的结果及假设的故障线路相符合，改进遗传算法定位正确。

2.2 多重故障

假设在图1所示的网络同时发生故障K1和故障K2。根据网络的连接关系可知，开关S4将无故障电流流过，其他开关流过与开关假定的正方向相同的故障电流。计算各个开关的开关函数值(s)。(s)和Ij的值如表1所示。

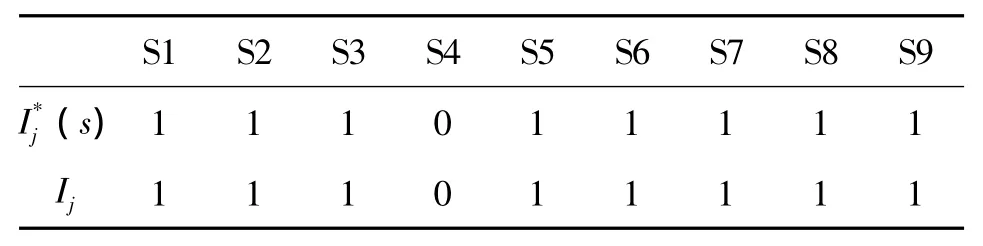
表1 两重故障时各开关的开关函数值和故障电流状态值Tab.1 Switching function value and the fault current state value of each switch for two fault

取ω为0.5，根据式 (3)计算适应度函数值如式 (6)所示。

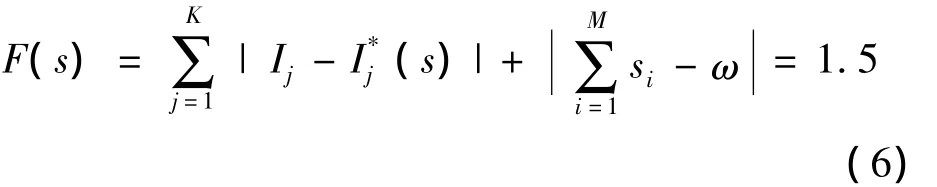
由FTU上传的故障电流越限信号可以确定各开关的Ij值，代入适应度函数，在遗传算法工具箱中求解适应度函数的最优解，仿真结果如图4所示。

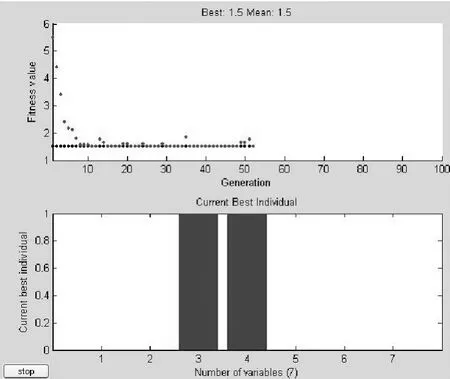
图4 故障K1和K2同时发生时的仿真结果Fig.4 Simulation results of fault K1 and K2 occuring simultaneously

由图4可知当种群经过52代的遗传操作时取得了最小的适应度值1.5。此时的最优个体为3和4，而个体3和4正好对应故障线路c和d，与理论计算的结果和假设的故障线路一致。改进遗传算法定位准确。

3 结论

遗传算法已经成功地在配电网故障定位中得以应用，理论证明其有较高的容错性。本文对网络中各个开关的正方向作了定义，并构造新的开关函数和适应度函数，进而将改进的遗传算法应用于含分布式电源的配电网故障定位。改进后的遗传算法能适应多变的网络结构。仿真分析验证了新算法的有效性。含分布式电源的配电网故障定位的研究目前还处于起步阶段，本文仅对新算法的有效性进行了有益的探索;由于配网复杂多变，算法的实用化还有待进一步研究。

[1]王进强，陈少华，尹雁和，等.含分布式电源的配电网故障区间定位算法[J].电力科学与工程，2011，27(2):25-29.Wang Jinqiang，Chen Shaohua，Yin Yanhe，et al.Fault region location algorithm for distribution network containing distributed generation[J].Electric Power Science and Engineering，2011，27(2):25-29.

[2]王飞，孙莹.配电网故障定位的改进矩阵算法[J].电力系统自动化，2003，27(24):45-49.Wang Fei，Sun Ying.An improved matrix algorithm for fault location in distribution network of power systems[J].Automation of Electric Power Systems，2003，27(24):45-49.

[3]杨俊起，陈滟涛，杨凌霄，等.配电网故障定位的改进矩阵算法研究[J].高电压技术，2007，33(5):135-138.Yang Junqi，Chen Yantao，Yang Lingxiao，et al.Study on improved matrix algorithm for fault location in power distribution network[J].High Voltage Engineering，2007，33(5):135-138.

[4]江道灼，张锋，张怡.基于配电监控终端的配网故障区域判断和隔离[J].继电器，2002，30(9):21-23.Jiang Daozhuo，Zhang Feng，Zhang Yi.Fault sections detection and isolation in distribution system based on FTU[J].Relay，2002，30(9):21-23.

[5]费军，单渊达.配网中自动故障定位系统的研究[J].中国电机工程学报，2000，20(9):32-34.Fei Jun，Shan Yuanda.Study of automatic fault location system in the distribution network[J].Proceeding of the CSEE，2000，20(9):32-34.

[6]肖健，王渺.一种应用于配电网络故障定位的混合算法[J].电力系统自动化，2000，24(8):57-61.

[7]杜红卫，孙雅明，刘弘靖，等.基于遗传算法的配电网故障定位和隔离[J].电网技术，2000，24(5):52-55.

[8]卫志农，何桦，郑玉平.配电网故障区间定位的高级遗传算法[J].中国电机工程学报，2002，22(4):127-130.

[9]严太山，崔杜武，陶永芹.基于改进遗传算法的配电网故障定位[J].高电压技术，2009，35(2):255-259.