压电柔性臂动力学模型修正研究

曹青松，王辉，洪芸芸，何悦海

(华东交通大学载运工具与装备教育部重点实验室，江西南昌330013)

工程实际中，几乎所有机器设备都处于振动环境中工作，如何改善、控制以及利用这些振动对国防建设、航空航天技术的研究以及工业技术的发展都具有重大意义［1］。要改善、控制和利用机械设备运转中的振动，首先需要建立准确描述结构系统特性的数学模型。在系统结构数学模型描述上存在理论建模与实验建模两种［2］，两种方式均存在一定误差，控制效果的好坏、系统的稳定与否在很大程度上都取决于系统的模型是否建得精确，从某种意义上说柔性多体系统的动力学建模是系统研究的核心问题，因此，对系统模型的修正具有重要意义。

传统的柔性臂建模，为了降低建模难度，在建模过程中简化了方程的推导过程和最终的推导结果，忽略了柔性臂的结构变化、关节摩擦、结构阻尼和导线因素的影响，因此模型与实际系统存在一定程度上的差异。目前，模型修正的主要方法有［3－6］:最优矩阵法、设计参数型法、频响函数法、神经网络法等。袁永新等［7］提出一种基于不完全模态测量数据同时修正有限元质量矩阵与刚度矩阵的有效数值方法，该方法运用代数特征值反问题的理论与方法，得到了满足正交关系及特征方程的最逼近有限元质量矩阵及刚度矩阵的唯一的修正质量矩阵与刚度矩阵 (最优修正矩阵)，表达式简洁，修正过程简单而且容易实现。卢菊洪等［8］用实验方法测得系统的相关模态参数，建立了基准 (未损)模型，借助模型刚性灵敏度实现对系统结构损伤位置及程度的识别。李明伟等［9］提出了基于频响函数的模型修正方法，该方法以设计参数为修正对象，避免了模态分析过程，而且不需要将有限元模型的频响函数与实验测得的频响函数进行匹配，仅需要少量实测的频响函数数据即可完成模型修正过程。何浩祥等［10］利用遗传算法对神经网络权值进行优化设计，使运算速度得到了大幅度的提升，提出了一种基于子结构与神经网络的递推模型修正方法，使之更为实用便捷。

作者以两连杆多压电片作动传感的柔性臂结构为研究对象，由于在初始建立的模型中，为了降低难度简化了方程的推导过程和最终的推导结果，忽略了柔性臂的结构变化、关节摩擦、附加质量、结构阻尼和导线等因素的影响，造成模型与实际系统存在一定程度上的差异，针对这种情况，对系统初始模型，在刚度与阻尼方面进行有效修正。

1 压电柔性臂动力学模型特性

根据外力不做功，将柔性臂当Euler梁处理，求得单个柔性臂动能:

势能:

拉格朗日方程:

其中:L=T－V。

M、m、I1、P11分别为柔性臂质量、柔性臂末端集中质量、臂截面惯性矩、臂1的一阶模态。将式(1)、式 (2)代入式 (3)得到单臂自由振荡模型与角频率ω表达式分别如式 (4)、(5)所示:

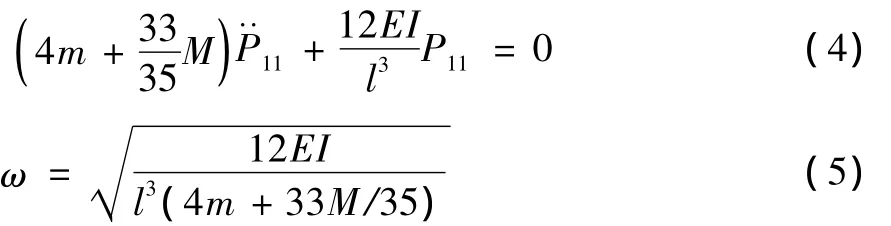
为了检测柔性臂的振动，将柔性臂根部固定于台钳上，在末端施加一个垂直冲击。这样只会激起臂的基本振型，不会激发其他任意振型。图1、图2为所得到的柔性臂的振动曲线。

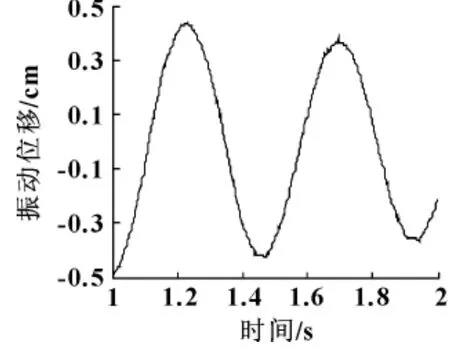
图1 柔性臂1弹性振动

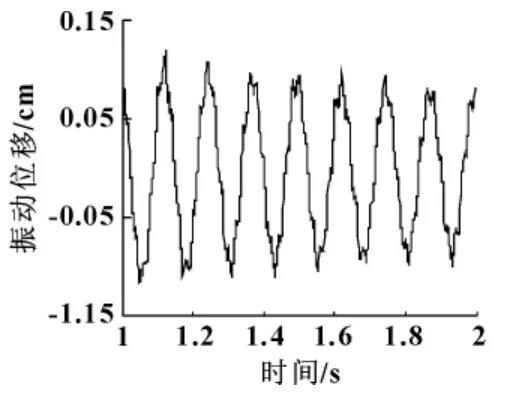
图2 柔性臂2弹性振动

柔性臂系统参数如下:柔性臂1长l1=0.35 m，宽b1=0.04 m，高h1=0.001 m，臂分布质量M1=0.11 kg，末端集中质量m1=0.19 kg，弹性模量E1=E2=200 GPa，惯性矩I1=3.33×10－12m4。柔性臂2的l2=0.32 m，宽b2=0.040 m，高h2=0.001 m，臂分布质量M2=0.075 kg，惯性矩I2=2.5×10－12m4。

将柔性臂数值参数代入式 (5)，得到臂1、臂2的振动频率，并与结构实际的检测振动频率 (图1、图2)一同列于表1中。

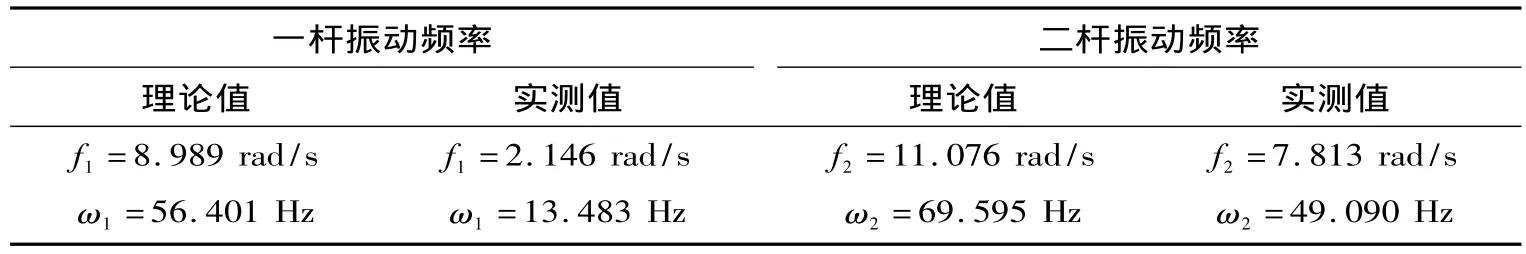
表1 柔性臂振动频率

自由衰减法是一种有效的常用的检测结构阻尼的方法，操作方法为:将柔性臂的根部固定，在末端施加垂直冲击，振动衰减率则表示为:

当阻尼为黏滞阻尼，或近似等效为黏滞阻尼时，则ε为一常数，与振幅无关。

表2 柔性臂衰减率

由表中频率数值可以看出角频率实际值与理论值存在着差异。导致这种差异的原因主要有两个方面，一方面是模型中柔性臂的长度与实际实验时柔性臂的长度有差异，在实验系统中台钳夹头的影响使柔性臂的长度小于理论长度，另一方面在实验系统中由于粘贴了压电陶瓷、导线等使柔性臂的物理特性参数E、J发生了改变，而在模型建立中忽略了这一方面的影响。同时臂振动也是不断衰减的，建模过程中忽略了系统的阻尼，是以等副变化来处理。

2 压电柔性臂模型及修正

为补偿频率上的差异，需对振荡模型进行调整，即在模型中增加刚度项:

于是得到刚度调整系数Δk的表达式为:

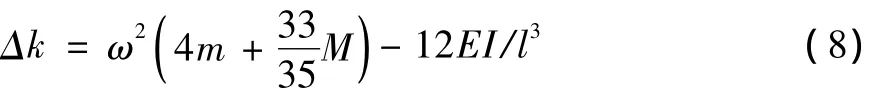
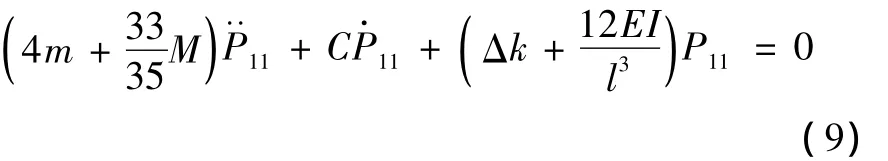
两联杆柔性臂多压电作动器数学模型如下式:

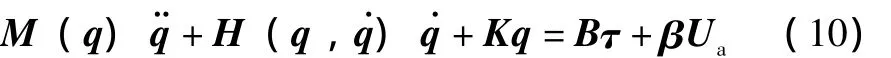
令Bτ+βUa=Q，由于惯性矩阵M为正定对称的，在这里定义G=M－1，在式 (10)中左右两边同时乘上G，则可见式 (10)写成:

根据广义坐标和广义力的定义，有:

将刚度矩阵用分块形式表示:

Kζ为4×4阶对角矩阵，定义Z=GH，O为零阵，P(t)=［p11(t) p12(t)p21(t) p22(t)］T，θ(t)=［θ1(t) θ2(t)］T，于是由式 (12)得:

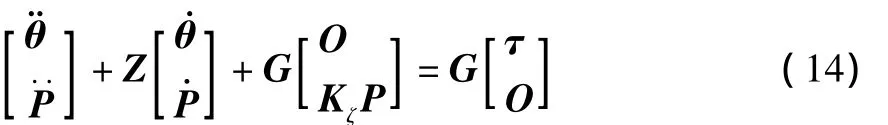
作如下分块化处理:

式中:Z11、G11为n×n维矩阵，Z12、G12为n×r维矩阵;Z21、G21为 r×n维矩阵;Z22、G22为 r×r维矩阵。

将补偿频率和增加阻尼的方法扩展到两连臂中去，综合式 (11)— (15)于是有:

为了研究简便，只研究其在某一固定构型时的弹性振动。通过上述公式的推导可知项与振动频率无关联，因此分析系统频率是可以忽略含的项。

由式 (16)得到的系统自由振动模型:

此式中G22Kζ不是对角矩阵，所以两柔性臂间的振动是耦合的。而又有 G22为对称正定，因此式(17)可以改写成:

由式 (18)有分量形式:

于是按照单臂修正分析过程对频率进行修正。在式 (19)中增加一刚度项

得到双臂振动刚度调整系数:

式中:ωij为第i根柔性臂第j阶振动角频率实测值。

测量电机在不同的转速下的柔性臂的振动角频率，将结果记录在表3中。

表3 (细分数)转速与ω间的关系

Z22中的为相对小量，此时又有˙θ=0，则可以认为Z22=0，于是由式 (18)并考虑到刚度调整有:

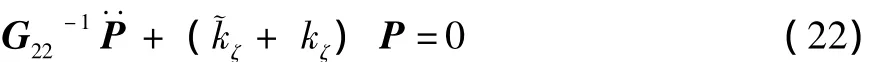
对上式增加阻尼补偿项:

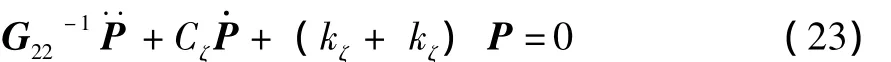
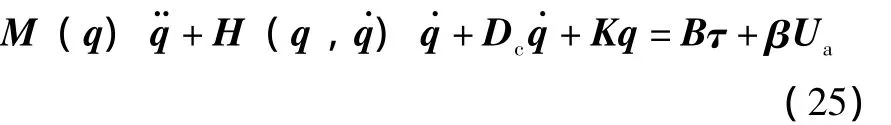
3 仿真与实验验证

为了验证系统动力学模型以及进行刚度调整与阻尼修正后系统模型的准确性，采用MATLAB软件对以上所建立的原始模型与修正模型进行仿真分析。在仿真过程中，将柔性臂系统相关参数代入，且大、小电机分别输出τ1=1.07n1sin(2πk1t)N*m(n1，k1为常数)，τ2=0.065n2sin(2πk2t)N*m(n2，k2为常数)。仿真过程中只考虑1阶模态修正，将衰减率与转角实测值代入各自修正公式，将所得的Dc˙q、Kq代入式 (25)。

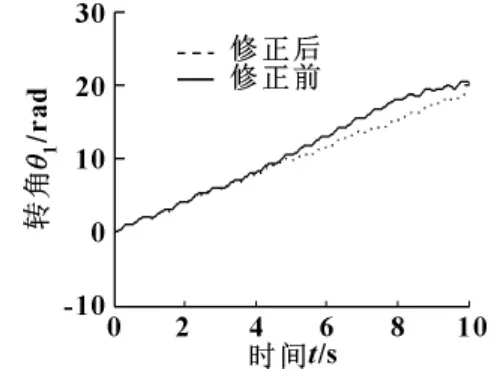
图3 臂1转角曲线

图4 臂2转角曲线

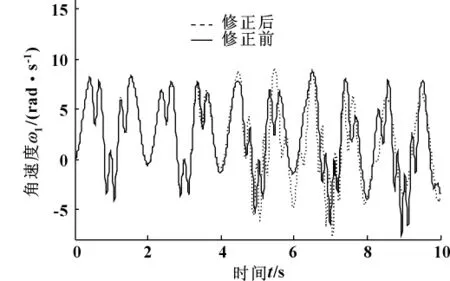
图5 臂1角速度曲线图

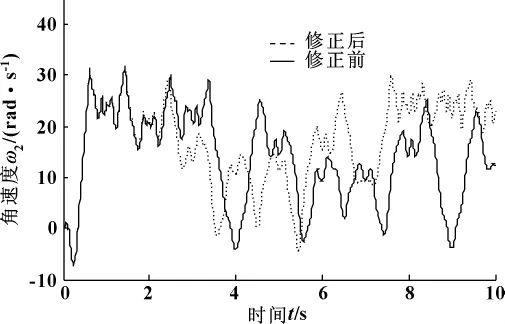
图6 臂2角速度曲线图

为了进一步验证所建立的动力学模型，将系统在脉冲力矩激励情况下的仿真结果和实验结果进行比较研究。在实验过程中，采集臂1振动信号时，臂2不转将其视为臂1末端集中质量，对臂1加垂直冲击;在检测臂2振动信号时，臂1照常转动，对臂2施加垂直冲击。在模型仿真过程中，设置系统初始状态与实验过程状态保持一致。实验与仿真的对比图如图7—10所示。

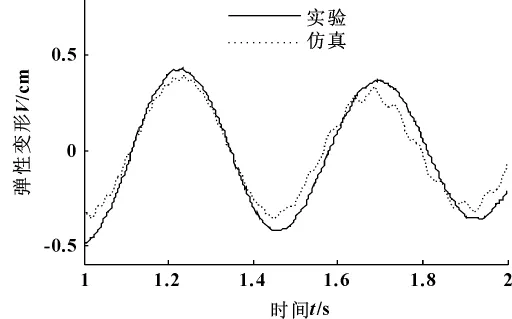
图7 修正前臂1振动比较

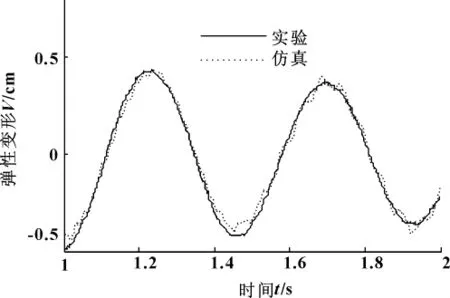
图8 修正后臂1振动比较

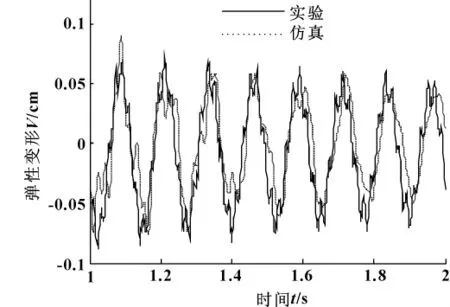
图9 修正前臂2振动比较

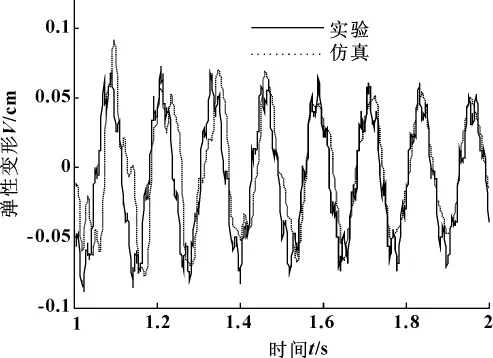
图10 修正后臂2振动比较

由上述仿真与实验结果可以看出:

(1)由图3、图4可知，模型修正前、后臂1、臂2转角曲线在线性度方面后者明显优于前者。线性度变化趋势在模型修正前与后两者之间变化明显，且修正后的曲线线性度更好，更接近现实模型的特性。

(2)臂2角速度曲线显示出较臂1更加明显的锯齿状波形，说明在臂2上产生的弹性抖动强烈，修正前、后的曲线如图5、6(频率为原始频率的0.5倍)所示:修正后曲线幅值波动更加平稳，因此刚度调整和阻尼补偿对模型的修正是有效的。

(3)图7与图8所示，臂1修正前后实验与仿真所得到的振动响应，对比修正前后结构发现，模型修正前臂1的冲击响应，修正前仿真结果的幅值略有偏小，衰减率与实验结果变化一致，但衰减周期较实验结果大;修正后臂1仿真的响应与实验结果无论是在幅值、衰减周期以及衰减率都高度吻合。臂2修正后的结果同样是幅值、衰减周期以及衰减率与实验结果相比较的吻合度高于修正前的。

4 结论

采用假设模态法描述压电柔性臂的弹性变形，再利用拉格朗日方程推导出系统动力学方程。通过刚度调整与阻尼补偿的方法对建模过程中采取的简化处理造成的模型误差进行修正。仿真结果表明，修正后的转角曲线线性度更好，角速度曲线幅值波动更加平稳，由此说明刚度调整和阻尼补偿对模型的修正是有效的。

【1】邱志成，韩建达，王越超．基于复合喷气压电驱动器的柔性机械臂振动控制［J］．机械工程学报，2009，45(5):184－192．

【2】KERMANI M R，MOALLEM M，PATEL R．V．Optimizing the Performance of Piezoeleetric Aetuators for Active Vibration Control［C］//Proeeedings of the 2002 IEEE Intemationa Conference on Roboties＆Automation．Washington，DC，2002:2375 －2380．

【3】MOTTERSHEAD J E，FRISWELL M I．Model Updating in Structural Dynamics:A Sutwey［J］．Journal of Sound and Vibration，1993，167:347 －375．

【4】HU Sau-Lon James，LI Huajun，WANG Shuqing．Crossmodel Method for Model Updating［J］．Mechanical Systems and Signal Processing，2007，21(4):1690 －1703．

【5】JOHN E M，MARYAM G T，YITSHAK M R．Assignment of Eigenvalue Sensitivities from Receptanee Measurements［J］．Mechanical Systems and Signal Processing，2009，23:193l－1939．

【6】YANG Y B，CHEN Y J．A New Direct Method for Updating Structural Models Based on Measured Modal data［J］．Engineering Structures，2009，31(1):32 －42．

【7】袁永新，戴华．用不完全模态测量数据修正有限元分析模型［J］．振动与冲击，2006，25(6):154 －156．

【8】卢菊洪，陈志平．基于有限元模型修正的损伤识别方法研究［J］．机械设计，2010，27(5):25 －27．

【9】李伟明，洪嘉振．基于频响函数的模型修正方法［J］．上海交通大学学报，2011，45(10):1455 －1459．

【10】何浩祥，闫维明，王卓．基于子结构和遗传神经网络的递推模型修正方法［J］．工程力学，2008，25(4):99－105．