数控微磨床热误差的补偿方法

舒启林，吕玉山，李玉龙

(1.沈阳理工大学机械工程学院，辽宁沈阳110159;2.沈阳理工大学汽车与交通学院，辽宁沈阳110159)

最近几年，在军事、航空航天及生物医药行业中，由于微型零件的加工需要，普遍期望设备能够更精巧，更加容易操作，需要能够加工微小复杂零件且精度较高的设备。因此，桌面化微型机床［1］的研制就显得十分必要。作者以自行设计的数控微磨床为研究对象建立热误差模型并进行误差补偿。该微磨床主要由超高转速的磨削主轴和工件主轴、自动微砂轮交换系统、伺服控制的微纳米进给工作台、微冷却系统、CCD图像高精密数控系统、识别监测系统所组成。该微磨床能完成各种微轴类 (φ100～φ1 000 μm)零件、孔类零件的磨削，其结构如图1所示。由于微磨床的精度要求非常高，各系统对温度的变化非常敏感，因此热误差对加工精度影响很大。为了减小微磨床的热误差，提高微磨床的加工精度与质量，文中将重点针对微磨床进行热误差建模并进行误差补偿。

图1 数控微磨床三维结构图

目前数控机床的热误差建模方法，如最小二乘法、时序分析法、聚类分析法、BP神经网络法等［2］，都需要建立与机床相应的模型，并且误差分析建模以及推导过程较为复杂，在建立的过程中也会受到人为误差因素的影响，有些误差模型很难建立。作者在研究国内外机床热误差模型建立情况的基础上，运用多元回归系统理论，根据自行设计的数控微磨床的热误差特性，建立数控微磨床热误差的数学模型［3－4］。这种热误差模型的通用性较强，推导过程简单，预测精度高，能够有效地补偿微磨床加工过程中的热误差，为微磨床的热误差补偿提供了简单有效的方法。

1 微磨床热源及热变形分析

数控微磨床由床身、y轴平台、z轴平台、刀具主轴、刀具、x轴平台、工件主轴、冷却系统、液压系统、电气系统等组成。

由图1可以看出，x、y及z轴平台沿3个互相垂直的坐标轴做直线运动，工件主轴和刀具主轴做高速旋转运动。

由于数控微磨床的独特结构，它在热源分布、对温度的敏感及热变形方向上也有其特殊性。微磨床在磨削运行过程中，由于刀具主轴与工件轴旋转、工作台往复以及诸多因素都会产生温升和热变形，从而使刀具主轴轴端和工件主轴轴端产生热位移，使微磨床刀具和工件的相对位置发生变化，影响磨削零件的形状和精度。此外，由于数控微磨床采用的是高速磨削，因此热变形的影响尤为突出。

为了清楚地掌握热源对微磨床各个轴的误差影响情况，为准确建立微磨床的热误差模型奠定基础，作者进行了刀具主轴、工件主轴和液压油、冷却液等热温升试验和热变形试验［5］。设定微磨床的刀具主轴测点为刀具主轴处;液压油、冷却液测点为油箱回油处;工作台测点为滚珠丝杆螺母处。热变形的测量是以床身为基准，分别测量微磨床全开工况从冷态到热车8 h后刀具主轴端面、工件主轴端面热位移，测点方向均为径向 (工件径向尺寸精度要求较高，故文中仅考虑微磨床径向热误差)，位移量向外延伸为正。图2为温度及热变形测点简图。

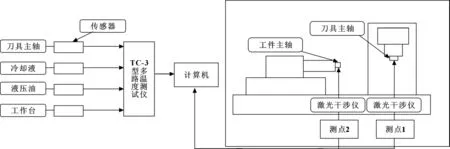
图2 热变形温升试验分布图

通过微磨床的热温升变形试验分析:微磨床的主要热源为刀具主轴高速旋转磨擦产生的热量，这是形成机床热变形的一个主要热源;其次是微磨床液压系统所产生的热量，及冷却液和工作过程中微磨床工作台往复摩擦导轨面所产生的热量。这些热敏感位置的温度变化及刀具主轴热变形如图3所示。

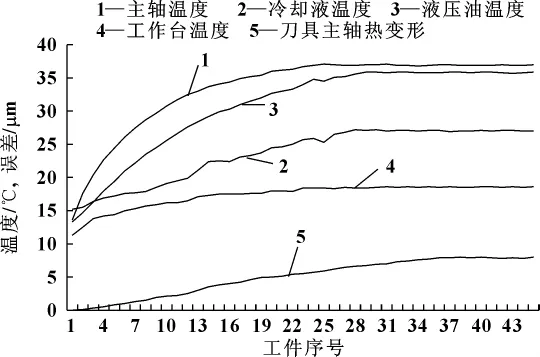
图3 微磨床热敏感位置温度变化

2 多元回归模型

2.1 多元回归理论分析

采用多元回归分析方法研究温度变化与热误差之间的关系。通过热敏感点的变化的温度预测热误差［6］。该模型能够有效地对高速磨削热误差进行补偿。多元回归模型如式 (1):

公式 (1)可以简单表达为下式:

式中:Y是系统输出 (热误差)，X是系统输入 (温度变化)，β是回归系数，ε是随机误差项。

为了得到有效的回归系数^β，可以使用最小平方法认为随机误差项ε为无穷小值。因此，为了得到回归系数的最小值，可以使用式(3):

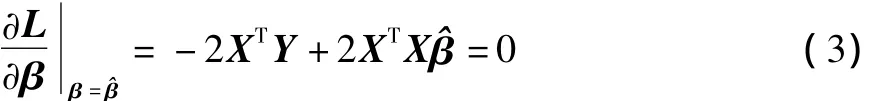
如果主要的温度变化不知道，应当寻找所有可行变量组合的域。在模型中，搜索域k，需要2k－1个可行的变量搜索周期和2k－1个被筛选的自变量。最佳温度变量的选择有助于提高模型的预测精度。最佳变量的选择需要一定的选择标准。

在回归模型中，判定系数R2被用于选择变量，并估计由自变量解释的因变量的方差的比例。此系数通过对因变量预测值和观测值的方差计算得到，其值在0～1之间。它反映了回归线逼近实际数据点的程度。当R2=1时，拟合线与原数据完全吻合。

文中选用4个因素作为温度变量和4个因素作为热误差变量来分析，因而，有28－1个变量组合被建立。最大R2的变量组合被定为最佳变量组合。

为了减少内存容量和提高计算处理速度，可以通过最小数量的变量组合和设置准许的残差平方和SSE(SSE=∑(Y－)2)的1.05倍SSEmax(R2)作为判定方程。通过在此范围内搜寻最小的R2，并且考虑到回归模型的最少输入变量。R2被定义为:

2.2 数据分析与建模

文中以刀具主轴的径向热误差为研究对象。图2展示了测量热误差和温度变化的实验平台，这个平台包括两部分:第一部分是利用激光干涉仪测量刀具主轴和工件主轴的径向热误差，测点分别在刀具主轴轴端和工件主轴轴端;第二部分是利用TC－3型多路温度测试仪测量热敏感位置的温度变化，测点分别在微磨床刀具主轴处、工作台滚珠丝杠处和液压油、冷却液的油箱回油处热源附近。对这些数据进行变量命名，见表1。

表1 温度变量和温度变化

为了在使用多元回归进行拟合时，提高拟合的精度，需要选择最佳变量组合为多元回归的拟合变量。最佳变量组合的选择方法在第2.1节中已经提到，主要是运用公式 (5)计算判定系数R2和公式SSE=∑(Y－)2计算参差平方和SSE。当R2越接近1，SSE越小时，观测值绕回归直线越紧密，回归方程对原数据的拟合效果越好。不同变量组合的判定系数见表2。

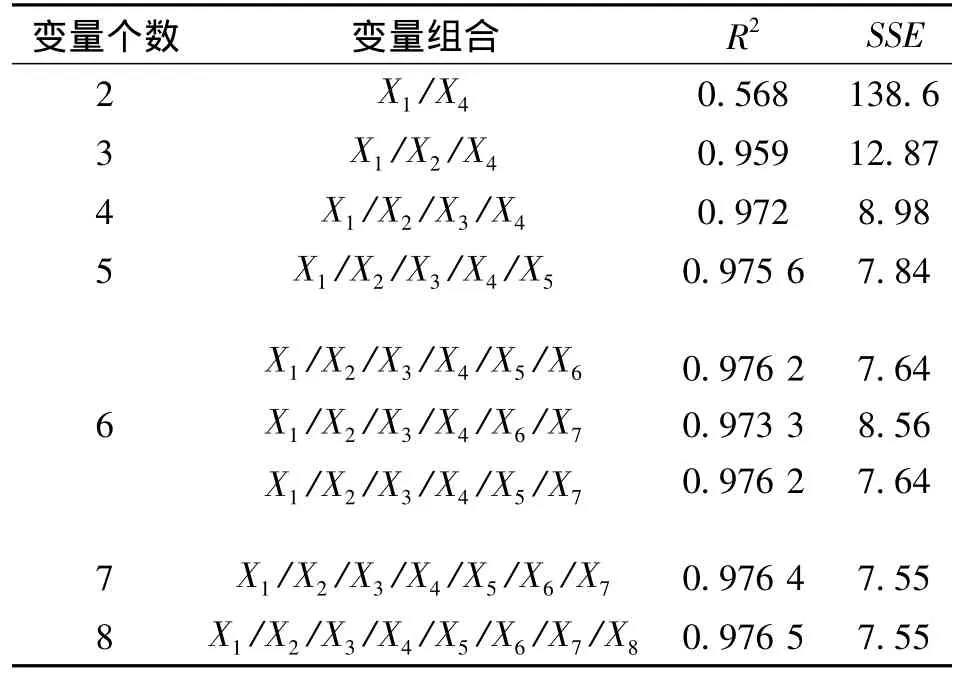
表2 不同变量组合的R2和SSE

通过比较可以看出:当在变量个数在6～8之间时，R2和SSE的值已无明显变化。因此，在满足多元回归模型精度的条件下，选择较少的变量个数，可以降低计算机所需内存，减少模型所需计算时间。最后得出:微磨床热误差补偿多元回归模型的建立，可以通过最佳变量组合X1/X2/X3/X4/X5/X6来实现。微磨床刀具主轴的径向热误差多元回归模型为:

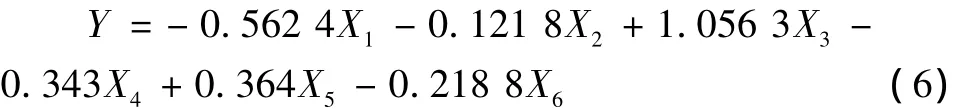
3 补偿系统

该数控微磨床热误差的补偿系统如图4所示，在微磨床热敏感位置布置温度测试仪，实时采集温度数据。温度信号经调整板放大、调整等处理后，由A/D板送入热误差数据模型。根据热误差数据模型算出补偿值后，将信息输入微磨床的PMAC控制系统。最终由PMAC控制系统对刀具位置进行补偿，达到补偿微磨床热误差的目的。图5为刀具主轴热误差补偿值和补偿效果曲线，图中曲线2为热误差补偿曲线 (经式 (6)计算得出)，即刀具位置补偿曲线，曲线3为补偿修正后的残差。最终，在此次研究中，微磨床刀具主轴径向热误差由8 μm减少到1 μm以内，补偿效果比传统的各类机床补偿系统有很大的提高。

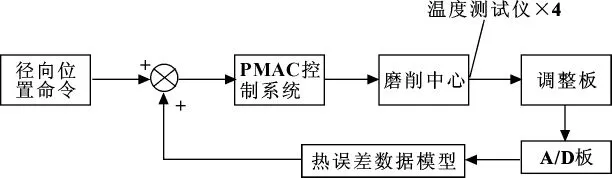
图4 数控微磨床热误差补偿控制系统

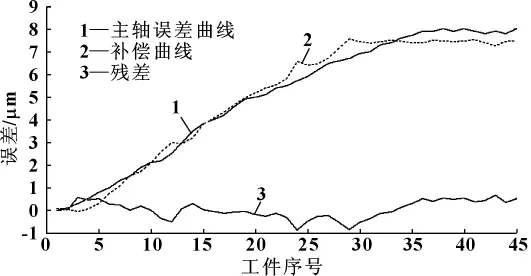
图5 热误差补偿效果

4 结论

作者提出的多元回归热误差模型已经证明能够有效地对数控微磨床进行热误差补偿，并得出以下结论:

(1)此次研究成功实现了使用多元回归模型在数控微磨床上进行在线热误差补偿。

(2)通过对微磨床进行热源分析得出热敏感点，并利用这些热敏感点的温度数据作为反馈信息。通过计算判定系数R2的最大值，找出最佳变量组合，使模型的变量个数减少至6个，节省了数控系统的内存空间，提高了计算速度。

(3)实验结果得出:数控微磨床刀具主轴的径向最大热误差由8 μm控制在1 μm以内。

【1】王鑫，舒启林，吕玉山，等．数控微磨床综合空间误差建模研究［J］．沈阳理工大学学报，2011，30(3):50 －54．

【2】章婷，刘世豪．数控机床热误差补偿建模综述［J］．机床与液压，2011，39(1):122 －127．

【3】WU Ching-Wei，TANG Chia-Hui，CHAG Ching-Feng，et al．Thermal Error Compensation Method for Machine Center［J］．Manuf Technal，2012(59):681 － 689．

【4】YAO Xin-hua，FU Jian-zhong，CHEN Zi-chen．Bayesian Networks Modeling for Thermal Error of Numerical Control Machine Tools［J］．J Zhejiang Univ Sci A，2008，9(11):1524－1530．

【5】盛晓尘，杨建国．数控磨床热误差实时补偿控制系统研制及应用［D］．上海:上海交通大学，2006．

【6】鲁远栋，丁国富，阎开印，等．数控机床热变形误差研究及补偿应用［J］．制造技术与机床，2007(4):25－29．