无先验知识下基于CHMM的刀具磨损监测技术

李威霖，傅攀，李晓晖

(西南交通大学机械工程学院，四川成都610031)

刀具智能状态监测技术作为先进制造技术的重要组成部分，是在现代传感技术与信号处理技术基础上发展起来的新兴技术。它可以降低制造成本，避免刀具的过度磨损对工件加工表面质量和尺寸精度的影响，实现加工过程自动化［1-3］。国内外许多学者致力于刀具磨损在线监测技术的研究，其中R TETI等［3］、J T ROTH 等［4］与 ABELLAN-NEBOT 等［5］分别从传感信号选择、信号处理与模式识别等角度总结了刀具磨损状态监测技术的发展现状。目前，刀具监测系统普遍需要刀具各磨损和破损状态的完备先验知识，将刀具磨损监测问题转换为单一的模式识别进行求解，关于无先验知识下的状态评估研究还鲜见报道。在实际加工现场中，受加工条件及成本等因素的影响，要提前获取各个工况下刀具磨损的全状态数据是较为困难的，这就导致传统的基于完备先验知识的刀具磨损监测模型建立困难，适用性差。因此，在无先验知识的情况下，研究如何有效地对刀具状态进行评估具有很高的实用价值。

刀具状态监测方法一般包括直接测量和间接测量两种，间接测量法更符合在线监测的要求［6］，因此文中采用基于三轴切削力与切削振动的间接测量方式。刀具监测信号带有很强的背景噪声，故障信息可能淹没在噪声中。采用小波包分析方法可以有效地抑制信号噪声，得到具有较高灵敏性的信号特征值［2］。因此文中采用小波包频带能量特征提取技术提取信号特征信息。

隐马尔可夫模型 (HMM)是一种不完全观测数据的统计模型，具有很强的时间序列建模及分类能力，特别适合于非平稳、重复性不佳的信号的分析。由于HMM在模式识别方面的良好表现，从20世纪90年代开始逐渐被引入到故障诊断领域，Antonio G VALLEJO Jr 等［1］、王玫等 人［7］、Kunpeng ZHU 等［8］与Huseyin M ERTUNC等［9］成功地将HMM用于刀具状态监测系统中。隐马尔可夫模型 (HMM)有诸多优势［5］:一方面HMM对动态过程时间序列具有极强的建模能力及时序模式分类能力，特别适合于非平稳、重复性不佳的信号的分析;另一方面，一个HMM参数由同类模式的训练样本得到，每一类模式对应一个HMM，具有较好的学习与再学习能力，适合非完备数据下的在线状态监测。因此，作者采用CHMM(Continuous Hidden Markov Model)实现无先验知识下的刀具磨损状态监测。

新刀经过短暂的磨合期后进入较长的正常磨损阶段，刀具处于正常磨损阶段的时间长、状态容易确定、数据易于获取。因为无刀具磨损先验知识，所以首先采用监测过程中的正常状态监测数据建立监测模型。根据刀具未知状态特性向量与监测模型间的对数似然度获取刀具性能指标PV，其大小反映了刀具健康状态。鉴于在实际加工过程中通常无法提前获得不同工况下的刀具磨损全寿命数据，为了验证该监测模型的有效性，作者采用实验方法获取了刀具磨损全寿命数据。实验结果表明:该方法能在只采用刀具正常状态数据的情况下对刀具的健康状态进行较为准确的评估，且所需样本数较少，训练速度快。

1 连续隐马尔可夫模型基本理论

采用连续高斯概率密度函数来模拟HMM中每个状态观测矢量的模型被称作连续高斯混合密度隐马尔可夫模型 (CGHMM)。一个HMM模型通常采用一个三元组λ=(π，A，B)来表示，CHMM也可以用类似的结构来表示。π为初始状态概率分布:

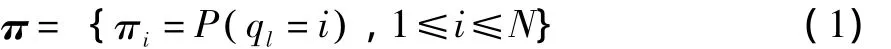
其中:N为模型中状态数。

A为状态转移矩阵:

B为输出概率密度函数:

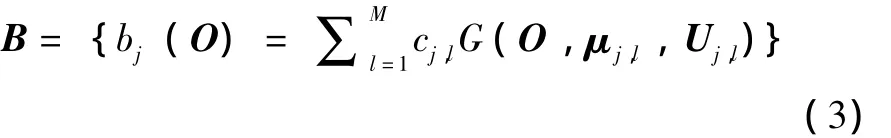
其中:O为观察向量D×T，M为每个状态包含的混合高斯元个数，cj，l为混合高斯元的权值，G为正态高斯概率密度函数，μj，l为均值矢量，Uj，l为协方差矩阵。

因此，可以用一个五元组来表示一个具有混合密度形式的 CGHMM:λ =(π，A，μj，l，Uj，l，cj，l)，其基本算法可以参考文献 ［10］。

上述算法是基于单观测序列建模的，如果要利用多个观察序列进行HMM建模，必须对上述公式进行修正。设由K个观测样本序列构成的集合表示为:

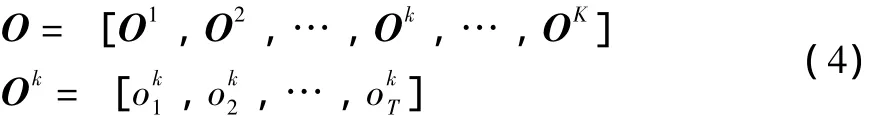
其中:k为观测样本序列，其观测时间长度为T。

定义过度概率:

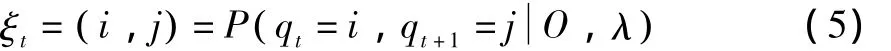
利用表达的前向概率和后向概率，可以得到过度概率，然后计算出CHMM模型的状态转移概率:

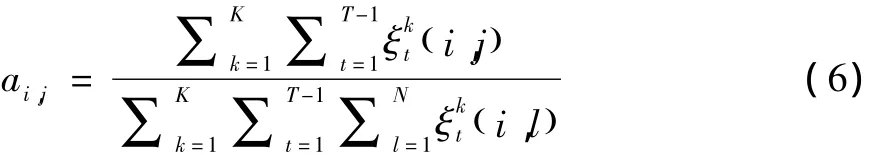
在迭代过程中，对于左右型HMM，一般不对参数π进行重估。

再定义γt(j，l)为某观测样本序列在t时刻处于状态j时第一个高斯元的输出概率:

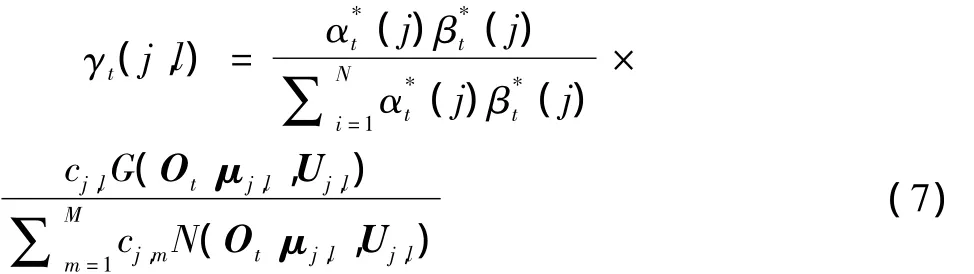
在单观测样本的情况下，公式的分母是恒定的，在后续的计算中，将在分式的分子和分母中被约去，可以省略。但是在多观测样本序列的情况下，由于不同观测样本序列对应的分母是不同的，因此不能简单地略去。由此可以得到下面的高斯混合密度函数的重估公式［11］:

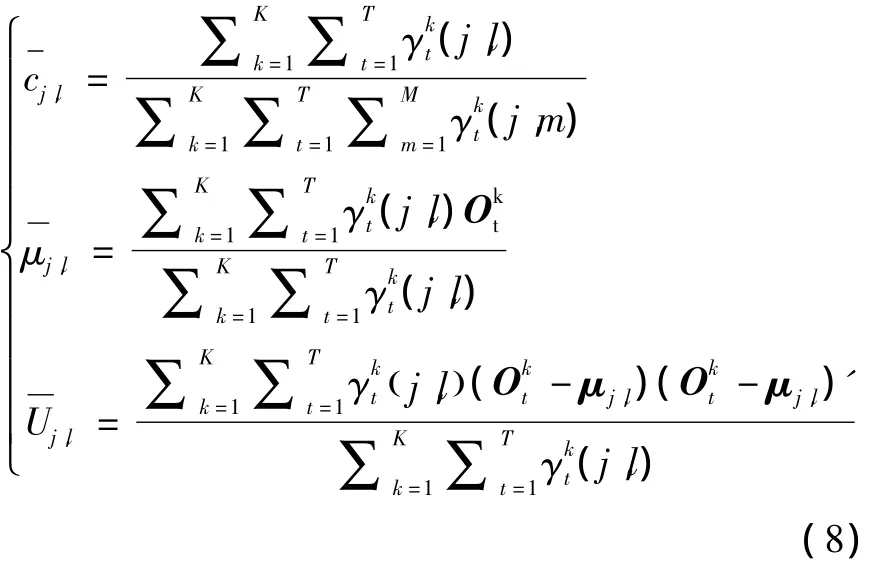
2 刀具状态监测系统设计

在无先验知识情况下，无法提前建立基于CHMM的监测模型，因此需要在监测阶段建立监测模型。根据刀具磨损退化规律可知，刀具进入急剧磨损阶段前会经历较长的正常磨损阶段。在该阶段，刀具磨损量随切削时间增长而缓慢增加，且比较稳定。也就是说，刀具处于正常磨损阶段的时间长、状态容易确定、数据易于获取，所以首先采用监测过程中的正常状态监测数据建立监测模型。整体思想为:随着刀具磨损量的增加，其观测序列与正常状态下的观测序列之间的相似度将逐渐减小，利用相似度获取刀具性能指标PV，进行状态评价。系统设计框图如图1所示。

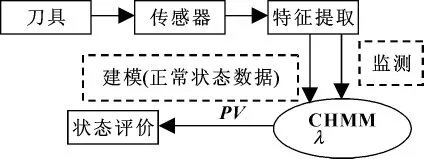
图1 刀具监测系统设计框图

整个系统可以归纳为以下3个部分内容:

(1)特征提取阶段。在该阶段利用小波包分析方法提取刀具切削力与切削振动信号的能量特征值，将其作为刀具状态监测的特征信息。

(2)模型训练阶段。新刀经过短暂的磨合期后进入较长的正常磨损阶段，该阶段较易判断。由于无刀具磨损先验知识，因此将监测过程中的正常磨损监测信号特征向量构成多组观测序列，用于训练CHMM，得到刀具状态监测模型λ。

(3)状态评估阶段。该阶段将未知状态监测序列输入已训练好的隐马尔可夫模型λ，利用Viterbi算法可得到其对数似然概率值为。设刀具正常状态下的观测序列输入模型所计算出的对数似然概率值为。

定义对刀具性能指标PV为:

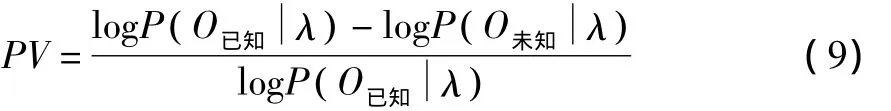
PV的大小代表了两个观测序列的相似度。若PV越小表示两个观察序列越相似，即刀具状态越接近正常状态。可以通过PV的大小来判断刀具所处磨损状态。

3 刀具状态监测实验与特征提取

3．1 监测实验方案

由于在实际加工过程中通常无法提前获到不同工况下的刀具磨损全状态数据。为了验证文中监测方法的有效性，采用实验方法获取了铣刀全寿命磨损数据。实验采用Röders Tech RFM760高速数控机床进行铣加工，实验实物如图2所示［12］。切削刀具为三刃球头铣刀，切削材料为HRC52不锈钢。Kistler三轴力传感器安装在工件与加工台间，配合Kistler电荷放大器测量加工过程中的切削力信息。Kistler三轴压电加速度传感器安装与加工台上。传感器的输出经NI DAQ PCI 1200板卡进行A/D转换后存入PC机硬盘。

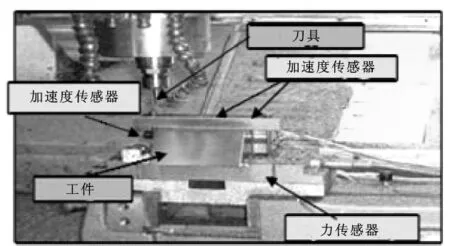
图2 刀具监测试验台

实验条件如下:主轴转速10 400 r/min，进给率为1 555 r/min，Y轴切削深度为0．125 mm，Z轴切削深度为0．2 mm，采样频率为50 kHz/channel。采用两把铣刀 (A、B)进行全寿命磨损试验。每次端面铣的长度为108 mm，记为一次走刀，每一走刀作为一次监测间隔，每个刀具进行300次走刀。每次走刀后采用LEICA MZ12显微镜测量刀具实际的后刀面磨损量作为刀具磨损结果。当刀具后刀面平均磨损量达到0．2 mm时，认为刀具磨钝。

3．2 基于小波包分析的特征提取

在加工过程中，由于铣削是多刃切削，而且材料的非均匀、加工过程的复杂性，导致了采集的动态信号具有很大的非平稳性。基于小波包分析的特征值观测序列能更加有效地提取非平稳成分中所包含的刀具磨损状态特征信息。图3给出了铣刀A第100走刀的切削力与切削振动Y轴时域信号。

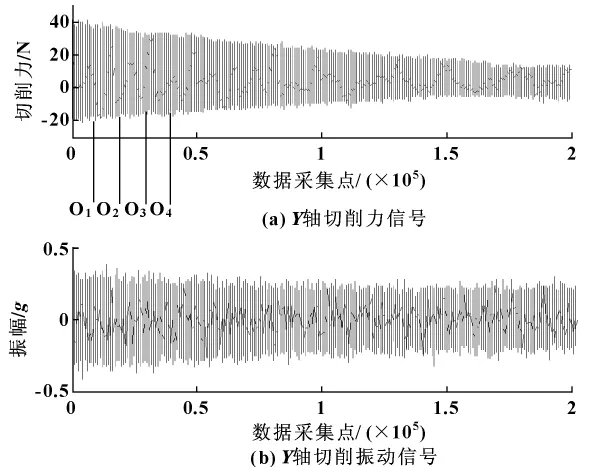
图3 铣刀A第100走刀监测信号时域图

根据实验条件可知，铣刀进行一次端面铣时，采集的数据长度在220 000左右，采用短时能量端点检测方法检测数据起始点，从起始点开始截取T帧用于刀具监测，T选择暂无标准，可根据实际情况而定，这里选T=20，每帧的数据长度为10 000点，移帧也为10 000点。图3绘出了铣刀A切削力前4个帧的分帧情况。

分帧完成后可以对信号进行小波包分解。经实验分析，对切削力信号采用db5小波基进行7层小波包分解，得到128个频段，然后求各频段的频带能量。采用第4、8和16频带能量作为切削力信号特征值。同理，对振动信号采用db9小波基进行7层小波包分解。采用第4、8、16、32频带能量作为切削振动信号特征值。由上述分析可知，每帧都有21个特征值。

3．3 特征值归一化处理

其中:x0为正常状态下的特征值平均值。

α的大小直接影响归一化曲线的陡峭度，当α越大时曲线越陡峭，归一化范围越小。应根据实际情况合理选择α的大小。文中对于切削力特征选取α=1．02，切削振动信号选取α=1．2。为了验证归一化方法的有效性，处理了第50～300走刀的信号。选取第50～60走刀数据作为刀具正常数据，根据归一化公式 (10)，可以计算出归一化数据。以铣刀A第50～300走刀的第一帧下的Y轴切削力第8频带能量特征为例，其归一化前后数据如图4所示。

频带能量特征值一般较大，将其用于HMM训练前需要进行归一化处理。在具有刀具状态完备先验知识的情况下，特征值归一化通常采用公式y=(xxmin)/(xmax-xmin)进行线性处理。当无先验知识时，特征值全局最大值与最小值无法获取，因此原方法不再实用。设刀具进入正常磨损阶段后，按照上述特征提取方法得到n个观测样本的特征向量。采用如下方法将数据归一化到 ［-1，1］范围内，归一化过程如下:

(1)求取这n个样本特征向量的平均值X0(每个特征值分别平均)。

(2)将正常状态及未知状态的监测特征值按照如下S函数进行归一化:

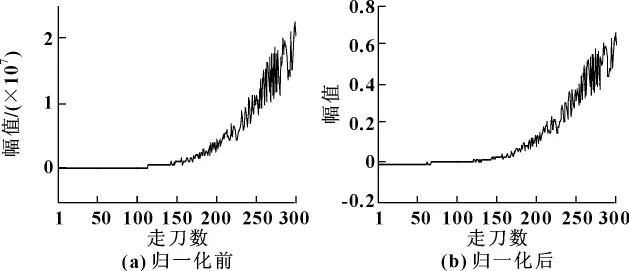
图4 切削力第8频带能量特征归一化前后对比图

从图4可见:该方法根据正常磨损阶段的第50～60走刀频带能量特征，成功地将第61～300走刀的特征进行归一化;并且从该特征值可以看出，随着刀具磨损量的增加，特征值成上升趋势。

4 基于CHMM的刀具状态监测

刀具磨损退化过程是一个渐变过程，刀具从正常到完全失效需要经历一系列不同的磨损退化状态。状态评估的主旨在于通过刀具监测信号评估隐藏在其背后的运行状态。文中采用监测过程中正常状态的特征信息建立CHMM，然后根据性能指标PV与评价规则判断刀具状态。为验证方法的有效性，使用了刀具全寿命数作为测试数据。具体操作流程如下:

(1)获得训练序列集。为了增加模型的适用性和鲁棒性，需要将每种状态对应的多个观测样本进行模型训练。取训练集的第50～60组数据作为正常状态训练数据，每组数据分20帧 (每0．2 s采集到的点组成1帧)，对每帧数据进行小波包能量特征提取，这样训练数据维数为21×20×10，即共10条训练序列，序列观测长度为20，每个观测点维数为21。

(2)模型初始化。由于小波能量特征的连续性和状态不可逆性，选择无跳跃的左右型CGHMM，经验选取4个隐含状态数。设置初始概率π=［1，0，0，0］。初始状态转移概率矩阵A为:

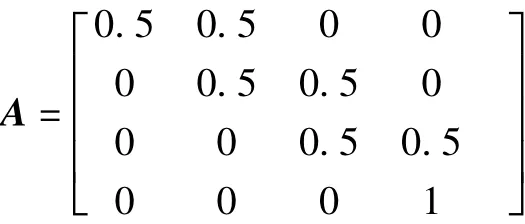
CHMM训练的精度受初始参数影响较大，尤其是观测阵B的初始值，B阵的初始值可由K均值算法迭代多次来获得。状态的观测概率由3个高斯概率密度函数联合决定。

(3)模型训练。将正常状态特征向量输入模型，采用上文所述的多观测序列改进算法进行训练，设置训练的最大迭代步数为20步，收敛误差e=0．000 5，经过4步迭代后训练结束。以铣刀A为例，其迭代过程如表1所示。

表1HMM训练过程

训练后的状态转移矩阵A如下:

(4)计算性能指标PV。利用Viterbi算法计算模型λ对N个正常状态观测序列的对数似然概率的平均值。将未知状态序列输入模型得到。根据公式 (9)得到刀具性能指标PV。分别将实验数据的第50～300走刀数据输入模型λ，并计算PV，其结果如图5所示。从结果可以看出:随着走刀数的增加，PV逐渐增大。

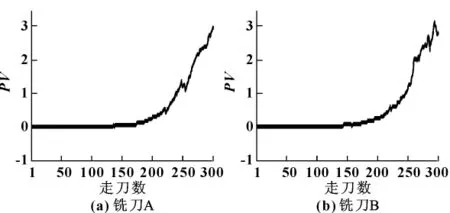
图5 第1～300走刀刀具性能指标PV变化图

(5)状态评估。该阶段根据性能指标PV评估刀具磨损状态。性能指标PV是一个连续变化量，它代表了刀具当前状态与其正常状态之间的相似度，所以能够反映刀具的性能变化。但相似度是一个比较模糊的概念，必须对该指标制定合理的报警阈值，作者从经验出发制定如下报警规则:

当2＜PV≤3，刀具处于严重磨损状态;

当3＜PV，刀具处于磨钝状态。

根据报警规则和图5所示PV可得到刀具磨损状态。铣刀A评估结果为:第271～300走刀刀具处于严重磨损。铣刀B评估结果为:第269～300走刀刀具处于严重磨损。

设刀具磨损量为大于0．15 mm时，刀具处于严重磨损阶段;磨损量大于0．2 mm时，刀具处于磨钝阶段。图6绘出了刀具时间磨损量曲线，可见根据报警规则对铣刀A的误判率为4．3%，对于铣刀B的误判率为0．67%。

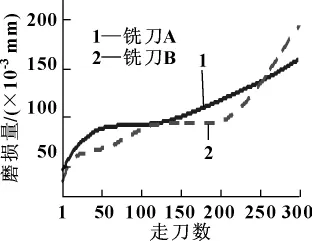
图6 第1～300走刀刀具磨损量曲线

5 结论

针对实际切削加工中刀具磨损完备先验知识获取困难，从而无法建立有效的全寿命监测模型问题，提出了无先验知识下对刀具进行状态监测的新方法。选择切削力与切削振动为监测信号，采用小波包分解技术提取信号特征，利用CHMM实现基于刀具正常状态数据的刀具状态监测。从实验结果可得到如下结论:

(1)提取能够反映刀具运行状态的特征信息是实现状态监测的前提，文中采用的小波包频带能量特征分析方法能够有效地提取基于刀具切削力与切削振动的特征信息。

(2)针对无先验知识下的归一化问题，采用了基于S函数的刀具特征归一化方法，成功实现基于正常状态刀具数据的刀具特征全局归一化。

(3)提出无先验知识下基于CHMM的刀具状态监测，采用性能指标PV作为刀具状态评估指标，能够较为准确地实现刀具磨损状态估计。该方法具有要求训练样本少、训练时间短、诊断速度快、扩展性好等优点。

【1】VALLEJO Jr Antonio G，NOLAZCO-FLORES Juan A，MORALES-MENÉNDEZ Rubén，et al．Tool-wear Monitoring Based on Continuous Hidden Markov Models［C］//Proceedings of CIARP，2005:880-890．

【2】LI Weilin，FU Pan，CAO Weiqing．Tool Wear States Recognition Based on Frequency-band Energy Analysis and Fuzzy Clustering［C］//Proceeding of 2010 Third International Workshop on Advanced Computational Intelligence，2010:162-167．

【3】TETI R，JEMIELNIAK K，O＇DONNELL G，et al．Advanced Monitoring of Machining Operations［J］．CIRP Annals-Manufacturing Technology，2010，59(2):717-739．

【4】ROTH J T，DJURDJANOVIC D，YANG X，et al．Quality and Inspection of Machining Operations:Tool Condition Monitoring［J］．Journal of Manufacturing Science and Engineering，2010，132(4):1-16．

【5】ABELLAN-NEBOT Jose Vicente，ROMERO SUBIRóN Fernando．A Review of Machining Monitoring Systems Based on Artificial Intelligence Process Models［J］．The International Journal of Advanced Manufacturing Technology，2010，47(1/2/3/4):237-257．

【6】DIMLA SNR Dimla E．Sensor Signals for Tool-wear Monitoring in Metal Cutting Operations:A Review of Methods［J］．International Journal of Machine Tools and Manufacture，2000，40(8):1073-1098．

【7】王玫，吕俊杰，王杰．基于连续高斯密度混合HMM的刀具磨损状态监测［J］．四川大学学报，2010(3):240-245．

【8】ZHU Kunpeng，WONG Yoke San，HONG Geok Soon．Multicategory Micro-milling Tool Wear Monitoring with Continuous Hidden Markov Models［J］．Mechanical Systems and Signal Processing，2009，23(2):547-560．

【9】ERTUNC Huseyin M，LOPARO Kenneth A，OCAK Hasan．Tool Wear Condition Monitoring in Drilling Operations U-sing Hidden Markov Models(HMMs)［J］．International Journal of Machine Tools and Manufacture，2001，41(9):1363-1384．

【10】RABINER L R．A Tutorial on Hidden Markov Models and Selected Applications in Speech Recognition［C］//Proceedings of the IEEE，1989:257-286．

【11】LI Xiaolin，PARIZEAU M，PLAMONDON R．Training Hidden Markov Models with Multiple Observations:A Combinatorial Method［J］．Pattern Analysis and Machine Intelligence，2000，22(4):371-377．

【12】LI X，LIM B S，ZHOU J H．Fuzzy Neural Network Modeling for Tool Wear Estimation in Dry Milling Operation［C］//Annual Conference of the Prognostics and Health Management Society，2009．