城市客运车辆双蓄能器式油气减振器特性建模与仿真
肖启瑞,石本改,唐拥林,黄学翾,王波群
(1.广东机电职业技术学院汽车学院,广东广州510515;2.广州地铁集团运营事业总部车辆中心,广东广州510000)
弹簧元件、减振器是车辆悬架系统中的关键部件,直接影响到车辆的平顺性和行驶稳定性,在普通轻型车辆悬架中,金属类弹性元件一般认为是线性的,液压减振器阻尼是非线性的。对于载重量变化剧烈而引起车体固有频率变化的城市客运车辆来说,传统金属线性弹簧与减振器的组合不能满足城市客运车辆高性能的要求。油气减振器具有集空气弹簧的变刚度特性以及普通液压减振器的非线性阻尼力的双重特性。基于此,作者对双蓄能器式油气减振器进行研究。
1 双蓄能器式油气减振器的数学建模
如图1所示,双蓄能器式油气减振器由下腔A、上腔B、活塞杆内腔C以及蓄能器D、蓄能器E组成。其中蓄能器D、E中充以一定压强的惰性气体,一般充以氮气。当活塞组件相对缸体向下运动时,下腔A液体压强升高,液体进入蓄能器E中压缩其中气体,从而“蓄能”。与此同时,上腔B体积增大,压强减小,蓄能器D中气体膨胀,将C腔液体通过活塞组件上的节流阀孔系压入上腔B,起到“补偿”B腔体积的作用,此过程液体应保持连续,避免减振器外特性发生“空程性畸变”。
同理,当活塞组件相对缸体向上运动时,上腔B中液体压强升高,液体通过活塞组件上的节流阀孔系压入C腔,再进入蓄能器D中压缩气体,达到复原行程“蓄能”效果。与此同时,蓄能器E中气体鼓胀,起到“补偿”A腔体积的作用。
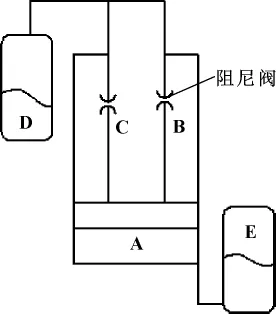
图1 双蓄能器式油气减振器结构
1.1 A腔液体压强的求解
由气体状态方程可知

式中:pe0、Ve0为蓄能器初始状态下的气体压强和体积;pe、Ve为蓄能器任意工作状态下的气体压强和体积;n为气体多变指数,取1.4。
下腔A与蓄能器E之间以油管连接,有一定的沿程压力损失,为精确建模,根据流体力学相关原理进行计算:

式中:Q为压缩行程中由A腔进行蓄能器E中的液体流量,Q=v·Ah;Ap为油管截面积;L为油管长度;dp为油管内径;ρ为液体密度;λ为沿程压力损失系数,它与液体雷诺数Re密切相关,工程上可由下式确定[1]:
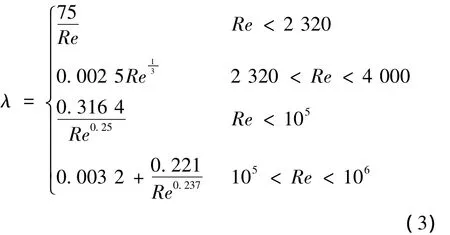
压缩行程时,活塞位移产生的体积增量由下式确定:

式中:ΔVE为蓄能器气体体积变化量。
在较高工作压强时,通常不能忽略液体的可压缩性,对于下腔A中液体的压缩量为:

式中:VA0为A腔液体的初始体积;k为液体的刚度;pA0为A腔液体的初始压强。
联立上述式子,得到A腔液体的压强pA。
1.2 B腔压强的求解
上腔B流入C腔的液体流量为:

工程上通常将减振器节流孔系视为薄壁小孔,薄壁小孔节流公式为:

由式 (6)、(7)可得两腔压强差为

下面着重分析该减振器阻尼孔系节流面积A0的处理,注意到在同类油气减振器模型中认为阻尼节流孔均为一个固定的面积,而轻型车使用的液压筒式减振器阻尼节流阀多为金属阀片式,节流面积随压差变化。由于油气减振器多用于重载荷的场合,使用金属节流阀片容易产生疲劳、损坏等不良后果。因此,作者将节流孔由金属阀片式改成实体阀式,在实体阀上加工若干个轴向节流槽,如图2所示。随着节流孔两侧液体压差ΔpBC的变化,阻尼节流孔的开度会相应地变化,相应的节流面积A0也发生变化,进而产生变化的阻尼效果。
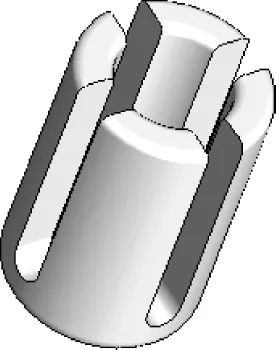
图2 实体阻尼节流阀结构
如图3所示,对处于任意位置的实体阀,节流面积为轴向环形分布的z个宽度为d的U型槽面积之和。总节流面积近似由下式计算:

式中:x为有流量通过时的实体阀位移,实体阀由复位弹簧平衡,有:

式中:x0为弹簧预压量;Af为实体阀有效截面积;kf为弹簧刚度。
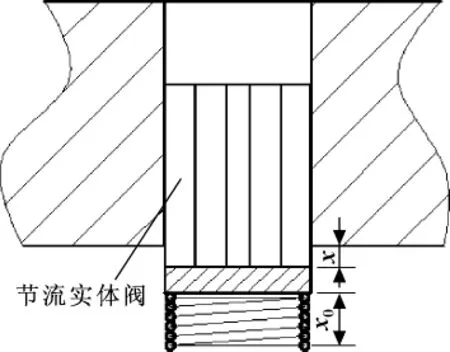
图3 实体阻尼节流阀尺寸结构
结合式 (6)— (10),可以得到ΔpBC的值,注意到实际上利用式 (7)进行实体阀节流孔流量压差计算只是工程上的近似,液压阀系试验表明此种U型槽阀孔的流量系数CD应该取0.7~0.76,而不是薄壁小孔节流时的0.62~0.68。
活塞内腔C与蓄能器D之间接以油管,油管的沿程压力损失也可用下式进行计算,方法同前:

要注意的是此时Q为由蓄能器D进入C腔的流量,Q=v·(Ah-Ag)。
1.3 蓄能器D工作状态分析
由气体状态方程可知

式中:pD0、VD0为蓄能器D初始状态下的气体压强和体积;pD、VD为蓄能器任意工作状态下的气体压强和体积;n为气体多变指数。整理得:

精确起见,考虑C腔液体的可压缩性,其体积压缩量为:

B腔容积的变化量应该等于C腔液体体积压缩量和蓄能器D内气体体积变化量之和,即:

联立上述方程得到B腔压强pB的表达式。完成A腔压强pA和B腔压强pB的求解后,根据受力分析可得活塞杆受力为
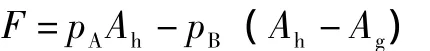
至此,已经完成双蓄能器油气减振器特性的数学建模。可以看出:双蓄能器油气减振器力学特性非常复杂,很难得到精确的解析解,应用Simulink进行油气减振器系统动态过程的求解是一种比较理想的方式。
2 双蓄能器式油气减振器性能仿真分析
取双蓄能器平衡位置初始气压为2 MPa,初始容积为3×10-3m3,单个油气减振器静态载荷为20 000 N。以一个速度为0.13 m/s的正弦信号作为油气减振器的仿真激励输入,可以得到油气减振器的力-速度特性以及力-位移特性如图4和5所示,此时对应油气减振器行程为166 mm。

图4 油气减振器的速度特性

图5 油气减振器的位移特性
由图5可以看出:在较低的激振速度时,油气减振器的复原行程与压缩行程的力-位移特性几乎是重合的,这是由于低频振动时,油气减振器阻尼特性表现很弱,两条位移曲线包围面积几乎为0,此时油气减振器对外主要表现为弹性特性,外特性上近似等效为一个空气弹簧,显然油气减振器的弹性特性曲线是非线性的,或者说是变刚度的,对载荷变化大的车辆尤为适用。
由图6可以看出:随着振动速度快,油气减振器位移特性复原行程和压缩行程曲线开始分离,速度越快,复原和压缩行程曲线分离越明显,二者包围面积越大,表示一个行程中所能吸收的振动能量越多,可理解为油气减振器高频振动时阻尼特性增强,振动速度达1.56 m/s时,其阻尼力明显增大。图7是振动速度对油气减振器速度特性影响曲线。
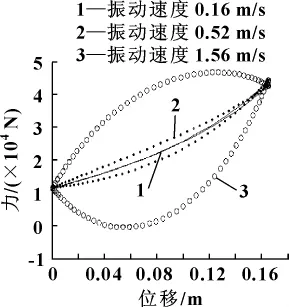
图6 振动速度对油气减振器位移特性影响
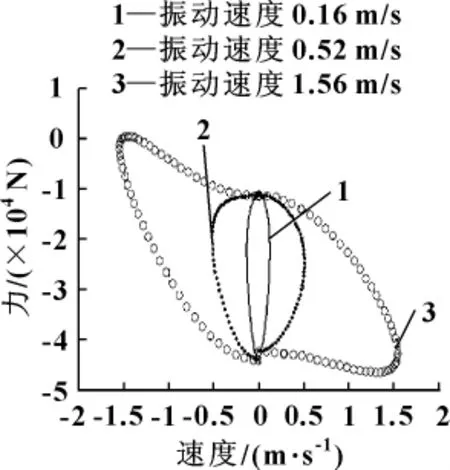
图7 振动速度对油气减振器速度特性影响
图8明确了节流阻尼孔径对油气减振器外特性影响。随着孔径增大,油气减振器位移特性复原行程和压缩行程曲线也表现分离,孔径越小,两曲线分离加剧,二者包围面积越大,这是由于阻尼孔径直接影响到液体节流阻力,较小节流孔径可得到较大的阻尼力,与普通汽车液压减振器特性一致,使油气减振器表现得较“硬”。

图8 阻尼孔径对油气减振器位移特性影响
随着蓄能器初始压强增大,油气减振器的刚度增大,这一点与空气弹簧特性非常类似。如图9所示。另外,随着油缸直径增加,油气减振器弹性特性越陡,也就是说刚度越大,结果如图10所示。

图9 蓄能器初始压强对油气减振器特性影响
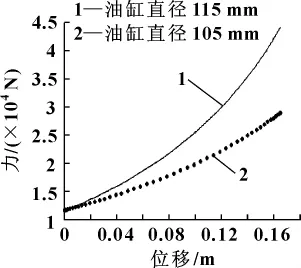
图10 油缸直径对油气减振器外特性影响
阻尼阀弹簧刚度与节流阻力有直接关系。阻尼阀弹簧刚度一般较大。随着弹簧刚度增加,位移特性曲线开始分离,表明阻尼力增大,如图11所示。

图11 阻尼阀弹簧刚度对油气减振器外特性影响
从图12可知,油气减振器的复原行程阻尼力明显大于压缩行程。可以避免悬架压缩时过大的阻尼力导致车辆平顺性变差,较大的复原阻力保证大部分振动能量消耗在复原行程内。
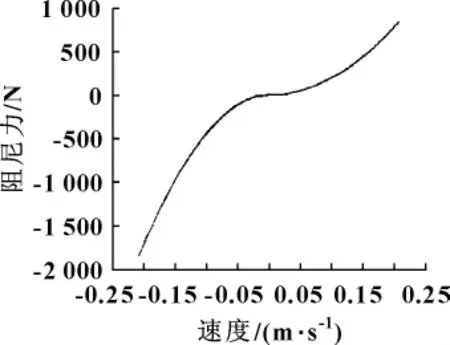
图12 油气减振器的阻尼力-速度特性
3 结束语
(1)得到了该型油气减振器的速度特性与位移特性。双蓄能器式油气减振器是一种集变刚度特性与非线性阻尼力的气、液耦合体,表现出不同的非线性刚度特性和不同的非线性阻尼,非常适合载重量变化较大的重型车辆。
(2)详细介绍了不同于一般车辆液压减振器阀片式的实体式阻尼阀;详细讨论诸如振动速度、节流孔径、蓄能器压强、阻尼阀弹簧刚度等关键参数对油气减振器性能影响;得到了减振器单纯阻尼力非线性速度特性曲线。
【1】马国清,檀润华.油气悬挂系统非线性数学模型的建立及其计算机仿真[J].机械工程学报,2002,38(5):96-97.
【2】封士彩.油气悬挂非线性数学模型及性能特性的研究[J].中国公路学报,2002,15(3):122 -123.
【3】肖启瑞.汽车减振器阀片挠度计算模型研究[J].客车技术,2011(1):34-36.
【4】梁贺明,陈思忠,游世明.油气悬架数学建模及仿真研究[J].计算机仿真,2006,23(6):241 -243.
【5】孙涛,喻凡,邹游.工程车辆油气悬架非线性特性的建模与仿真研究[J].系统仿真学报,2005,17(1):210-211.

