基于梯度校正法的非对称液压缸建模与参数辨识

谢建，李良，黄建朝

(第二炮兵工程大学，陕西西安710025)

在导弹起竖液压系统中，液压缸的行程较长，为节约空间都是采用非对称液压缸，并且这种液压缸的加工、密封都比较简单，制造成本也较低，更适合一些结构尺寸要求严格的导弹武器地面发射设备。但非对称液压缸两腔的有效工作面积不等，因而正反向运动时，系统所需流量不等，各种参数与对称缸差异很大，描述工作油路的数学模型也不同［1］。所以非对称液压缸建模问题是近年来国内理论界关注的一个热点问题。

以往对于非对称液压缸的模型研究主要沿用对称缸的方法，把重点集中在负载压力和负载流量的定义上，其实质就是通过变量整合实现微分方程的整合［2］。由于这种方法不能反映系统结构因素对模型的影响，所以建模误差较大。系统辨识和参数估计是一种建模的有效手段。作者用梯度校正法对阀控非对称液压缸系统进行了辨识，得到了其传递函数模型，并进行了算法的验证，为起竖液压缸控制的进一步研究奠定了基础。

1 非对称液压缸模型的建立

在进行系统辨识之前，需要根据已经掌握的知识得到模型的结构。对于阀控非对称液压缸系统，可以利用液压系统的相关理论和公式推导得到系统的数学模型，指导后面系统辨识和参数估计。

由比例阀的负载流量方程、液压缸流量连续性方程和液压缸力平衡方程得:

式中:QL为负载流量;pL为负载压力;Cte为等效泄漏系数;Ck为附加泄漏系数;y为液压缸位移;Vt为等效总容积;B为液压缸等效阻尼系数;Fl为等效外负载力。

对式 (1)进行LapLace变换得:

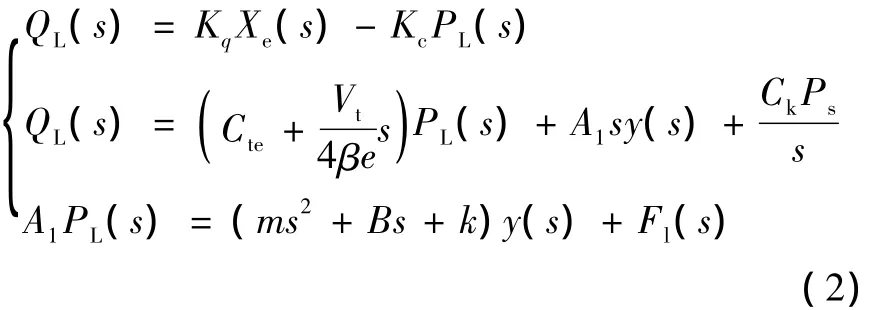
对式 (2)进一步简化得:

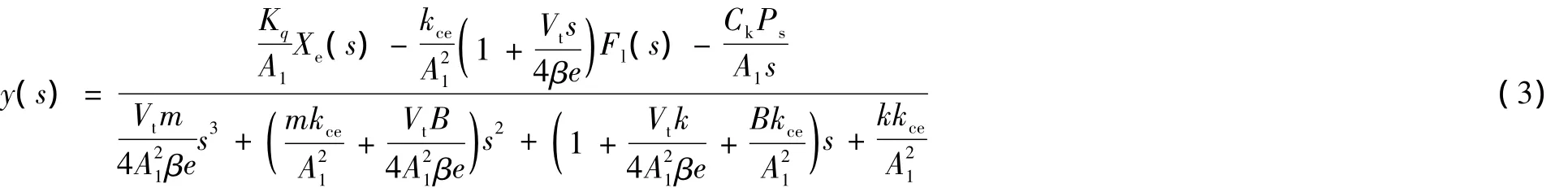
式中:kce为总流量压力系数，kce=Kc+Cte。

阀控非对称液压缸系统以惯性负载为主，没有弹性负载或弹性负载很小，因此可以认为k=0，则式(3)变为:

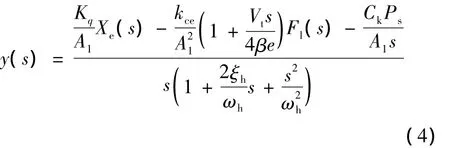
式中:ωh为阀控非对称液压缸系统固有频率，ωh=;ξh为阀控非对称液压缸系统阻尼比，ξh=

由式 (4)可以看出，阀控非对称液压缸系统是一个三阶系统。

2 梯度矫正参数估计的基本原理

梯度校正法的基本思想是:沿着准则函数 (目标函数)的负梯度方向，逐步修正模型参数估计值，直至准则函数达到最小值，该参数估计算法简单易懂、实时计算量小。可以描述为:

根据前面的推导可知阀控非对称液压缸系统是一个三阶系统，其离散传递函数可以描述为:

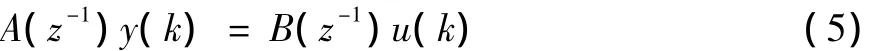
式中:u(k)和y(k)分别是系统的输入和输出;

A(z－1)=1+a1z－1+a2z－1+a3z－1;B(z－1)=b1z－1+b2z－1+b3z－1，a1，a2，a3，b1，b2，b3便是要估计的参数值。

式 (5)又可表示为:

式中:

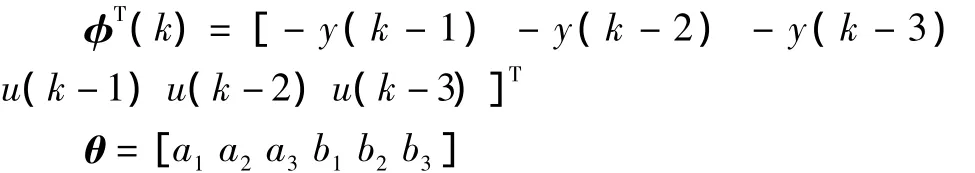
假设系统参数估计为:

上式γ的选择应能够使下式成立，即:

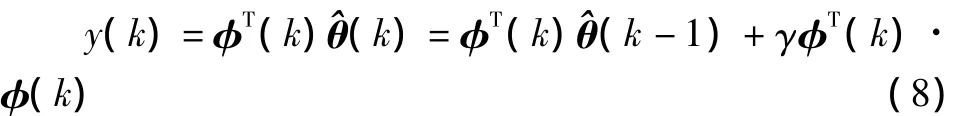
由式 (8)可以推出:

将式 (9)代入式 (7)得到:

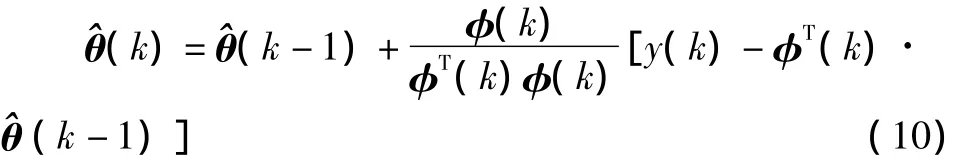
上式本质上是梯度校正法［3］。为避免φ(k)=0时算法不可行，式 (10)常修正为

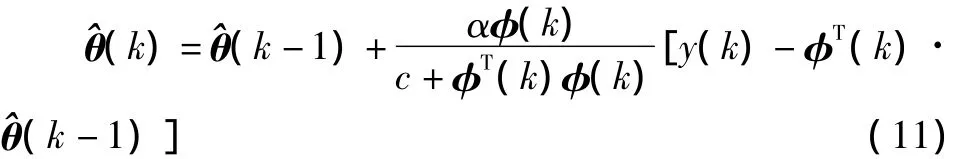
式中:c＞0，0＜α＜2。

梯度校正参数估计的步骤如下:

步骤1，设置初值^θ(0)及参数c和α，输入初始数据;

步骤2，采样当前输出y(k)和输入u(k);

步骤3，利用式(11)计算^θ(k);

步骤4，k→k+1，返回步骤2，继续循环。

3 非对称液压缸模型参数估计

3.1 输入信号的选取

对于任何系统辨识算法，对输入信号的选取都有一个基本原则:输入信号必须持续激励辨识系统的所有模态。若系统模型的结构正确，系统模型的辨识精度直接通过Fisher信息函数矩阵依赖于输入来确定。因此，合理地选择系统辨识的输入信号是保证辨识精度的重要环节［4］。

系统辨识中广泛采用的输入信号有白噪声序列、M序列、逆M序列。理论分析表明，选用白噪声序列可以保证获得较好的辨识效果。因为液压系统对输入信号的响应需要一定的时间，若输入信号变化太快则系统不能跟随上输入信号，使得系统的辨识信息丢失，从而导致辨识的失败，所以在每个白噪声序列点延迟一定的时间，通过实验确定延迟时间为0.3 s。输入的白噪声序列如图1所示。

图1 输入白噪声序列信号

3.2 实验设计及数据采集

由于现在还很难得到关于导弹起竖液压系统的有效数据，所以作者采用实验室的FESTO液压实验平台搭建阀控非对称液压缸系统来模拟起竖液压系统。其实验原理如图2所示。

图2 液压实验系统原理图

采用NI公司的PCI6221作为数据采集设备，其分辨率为16位，最大采样频率为250 kHz，实验所用频率为1 kHz，即1 s内采集1 000个数据点。实验中计算机通过LabVIEW平台输出白噪声序列信号到采集卡PCI6221来控制电液比例阀，比例阀控制非对称液压缸的伸缩，液压缸上装有线性位移传感器，通过PCI6221采集液压缸的位移信号到计算机并存储位移信号备用，位移信号为电压信号，幅值为0～10 V，对应液压缸的行程为0～200 mm。

3.3 参数辨识

用图1中的输入白噪声序列信号，运行9.6 s，采集得到液压缸的位移信号如图3(a)所示，信号含有一定的噪声，为了提高辨识的精度需对信号进行滤波处理，图 (b)为滤波后的信号。

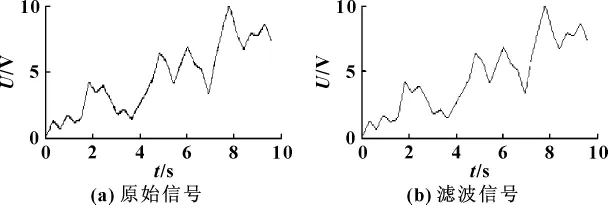
图3 液压缸位移信号

根据梯度校正法的基本步骤在MATLAB中编写辨识算法，以图1中的白噪声序列为输入信号，以图3(b)中的液压缸位移信号作为输出信号进行参数辨识，最后得到阀控非对称液压缸的模型参数为:

系统的离散传递函数为

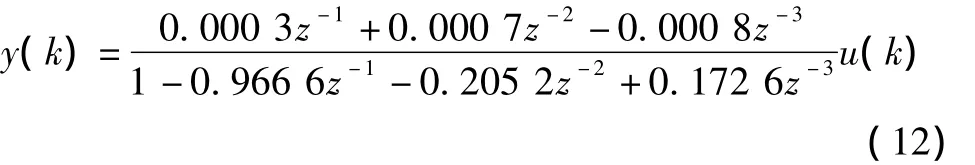
3.4 算法验证及结果分析

如图4所示，(a)为实验得到的位移信号和由辨识模型计算得到的输出信号的结果对比，(b)为误差信号，可以看出误差控制在0.03 V的范围内。

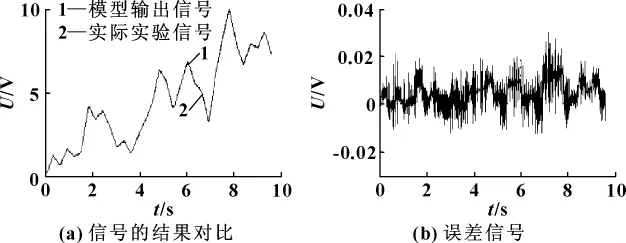
图4 算法验证1

为了充分说明方法的有效性，对其进行了更进一步的验证，改变输入白噪声序列，将模型计算得到的输出信号和实验实际采集的液压缸位移信号进行对比，如图5所示。

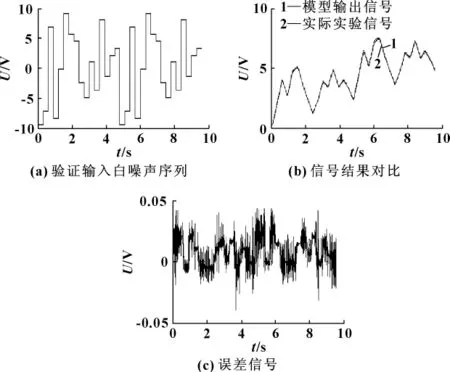
图5 算法验证2

通过对比模型输出信号和实际实验信号，证明辨识得到的模型是正确的，可以很好地反应输出信号。

4 结论

阀控非对称液压缸的模型是一个三阶系统，通过实验采集了输入输出信号，并用基于梯度校正的参数辨识方法对模型的参数进行了辨识，最后进行了算法的验证，证明此方法是可行的，为下一步建立导弹起竖液压系统的模型和进行起竖控制奠定了基础。

【1】吕云嵩．阀控非对称缸频域建模［J］．机械工程学报，2007，43(9):122 －126．

【2】赵周礼，周恩涛，周士昌，等．非对称缸系统精确建模方法研究［J］．机床与液压，2002(1):92－94．

【3】庞中华，崔红．系统辨识与自适应控制MATLAB仿真［M］．北京:北京航空航天大学出版社，2009．

【4】侯媛彬，汪梅．系统辨识及其MATLAB仿真［M］．北京:科学出版社，2004．

【5】蒋威，高钦和，李天义．基于最小二乘法的比例阀建模和参数辨识［J］．机床与液压，2011，39(5):113 －114，124．

【6】倪博溢，萧德云．MATLAB环境下的系统辨识仿真工具箱［J］．系统仿真学报，2006，18(6):1493 －1496．