倒圆角直梁型柔性球铰柔度计算与分析

杨春辉

(华东交通大学轨道交通学院，江西南昌330013)

柔性铰链具有体积小、无机械摩擦、无间隙和高灵敏度的特点，被广泛地应用于微操作机构，如今柔性铰链已经广泛应用在航空工业、自动化工业、生物医药、计算机和光导纤维等领域，具体应用有光学调整装置、盒式天平、小型力敏元件微加速度计、显微镜支架、MEMS、高精度微位移工作台等。

柔性铰链分为单轴柔性铰链和双轴柔性铰链。常见的单轴柔性铰链有两种:直梁型柔性铰链和圆弧型柔性铰链。直梁型柔性铰链有较大的转动范围，但运动精度较差;而圆弧型柔性铰链的运动精度较高，但转动范围相对小［1］。为了兼顾运动精度和运动范围，又衍生出下面几种转动柔性铰链:抛物线型柔性铰链、椭圆型柔性铰链、双曲线型柔性铰链等［2］。1965年，PAROS等已经推导出柔性铰链的简化计算公式［3］，主要对特定柔性铰链结构的不同的性能指标进行研究。吴鹰飞等给出了一般柔性铰链和直圆柔性铰链的计算公式［4］;LOBONTIU研究了倒角柔性铰链刚度指标［5］;SMITH 等［6］和陈贵敏等［7－8］对椭圆柔性铰链的性能开展了研究;XU等使用有限元方法对直圆、导角和椭圆这3种型式的柔性铰链的精度做了分析比较［9］。柔性球铰是一种双轴柔性铰链。LOBONTIU 等［10］、侯文峰［11］对多轴柔性铰链进行了研究，给出了柔度和回转精度的解析式，并利用有限元软件和试验对柔度公式进行了验证。董为将通常的球副型柔性铰链拉长，从而提供普通柔性铰链所不具备的大行程［12］。

作者以直梁柔性球铰为对象进行研究，以力学的卡氏第二定理和微积分为理论基础对柔性球铰的柔度计算公式进行推导，并用有限元方法验证了公式的正确性;在此基础上，分析各设计参数对柔性铰链柔度的影响，为直梁柔性球铰的设计提供了理论依据。

1 直梁型柔性球铰的柔度计算

图1为直梁型柔性球铰的结构参数，柔性球铰的参数如下:圆角半径为r、最小厚度为t、直梁长度为l。梁的有效长度为L=2r+l。

柔性球铰相对于主轴、次轴和纵轴是对称的，并定义主轴为z轴方向，次轴为y轴方向，纵轴为x轴方向。该铰链的局部坐标系Oxyz的原点建立在铰链的左端中心1处，其原点O与1重合。图1中的1—2段和4—5段都为角圆形部分，2—4段为直梁部分，3为该铰链的几何中心即回转中心。该铰链的自由端1 受力 F1x、F1y、F1z和力矩 M1x、M1y、M1z的共同作用。其受力分析如图2所示。

图1 直梁柔性球铰的结构参数

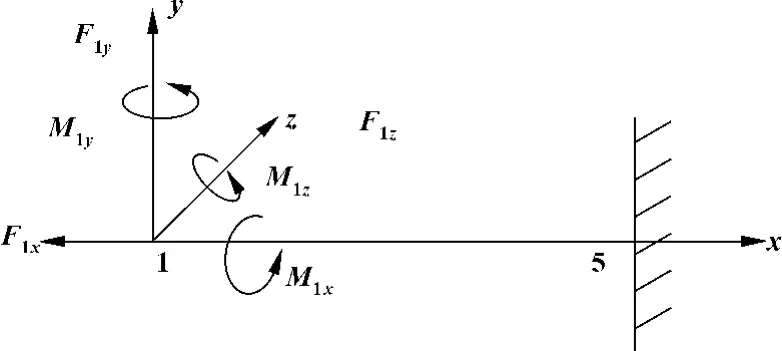
图2 直梁柔性球铰受力分析

运用卡氏定理，可以得到柔性球铰自由端的变形的数学表达式

式中:

柔性球铰结构的应变能为:

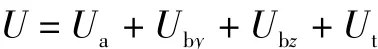
式中:Ua、Ubz、Uby、Ut分别表示轴向拉伸应变能、对z轴的弯曲应变能、对y轴的弯曲应变能、扭转应变能，分别可以表示为:

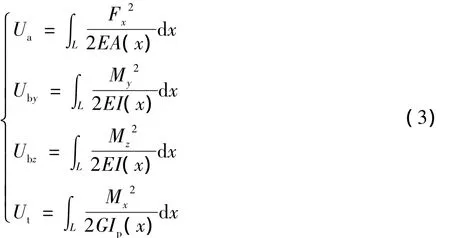
式中:E为弹性模量，G为剪切弹性模量，I(x)为惯性矩，Ip为极惯性矩。Fx=F1x，My=M1y+F1zx，Mz=M1z+F1yx，Mx=M1x。

柔性球铰的厚度t(x)可表示为:

柔性球铰绕y轴的角变形与绕z轴的角变形，以及沿y轴线形变形与沿z轴线形变形计算方法相同，因此只推导铰链绕z轴的角变形和沿y轴线形变形。

1.1 绕z、y轴方向的转动柔度公式

绕z轴的偏转角αz由两部分组成:由力矩M1z作用产生的角变形和由力F1y作用产生的角变形。1点处产生绕z轴的偏转角αz为:

在弯矩 M1z作用下柔性铰链的柔度 Cαz－Mz为:

式中:

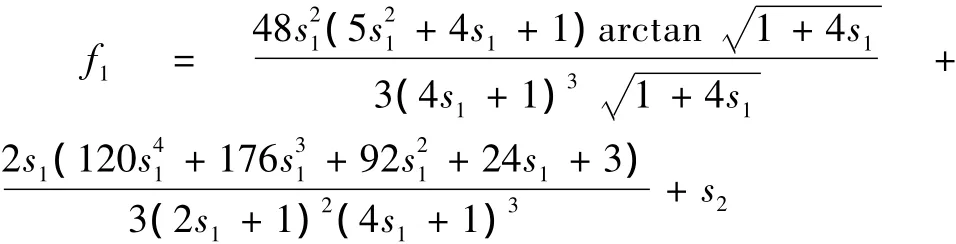
在力F1y作用下柔性铰链的柔度为:

同理可得绕y轴方向的转动的柔性公式为:

1.2 绕x轴方向的扭转柔度

在转矩M1x作用下，球铰产生沿x轴的扭转变形。其扭转柔度为

1.3 沿y、z轴的平动柔度

在弯矩M1z和外力F1y的作用下，弹性铰链除了绕z轴转动外，还会沿y轴产生变形Δy。沿y轴的线变形Δy为:

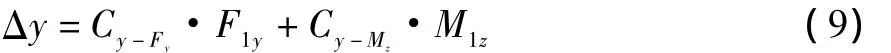
力F1y作用产生线变形Δy，其柔度表达式为:

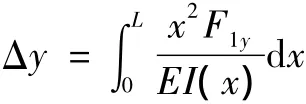
其中:f2、f3、f4为中间变量，其表达式为:

力矩M1Z作用产生角变形Δy，根据互等定理，其柔度表达式为:

1.4 沿x轴的平动柔度

沿x轴的线变形是由力F1x作用产生的，即:

其柔度表达式为:

2 有限元验证

利用有限元分析软件ANSYS10.0建立柔性球铰的模型，如图3所示。在柔性铰链的左端进行全约束，力Fx、Fy、Fz及力矩 Mx、My、Mz分别加载到右端5点处。单元类型为Solid45，有限元的实验参数为E=130 GPa、u=0.3、r=1 mm、l=3 mm。

图3 有限元模型

柔性球铰的有限元分析和解析计算部分结果比较如表1所示，由表中数据可知，有限元法和解析计算结果的偏差在16%以内。

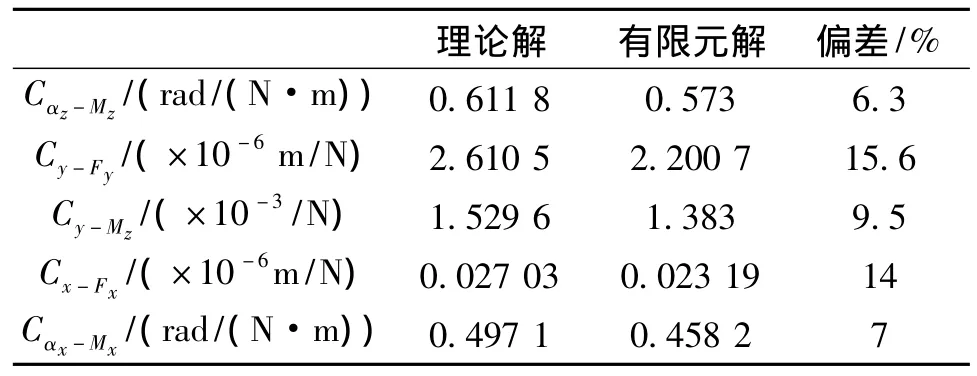
表1 有限元分析与解析计算部分结果的比较

3 性能分析

通过分析直梁型柔性球铰柔度公式可知:所有的柔度参数都与弹性模量E成反比。柔度非线性决定于半径r、长度l及最小厚度t等参数。图4—7中的基本参数是:l=8 mm、r=1 mm、t=1 mm、E=200 GPa。

图 4 柔度 Cαz－Mz和 Cαx－Mx随参数 t的变化关系

图5 柔度 Cαz－Fy和 Cy－Fy随参数 t的变化关系

图6 柔度随参数l的变化关系

图 7 柔度 Cαz－Mz和 Cαx－Mx随参数 r变化关系

由图 4—5 可以看出:柔性球铰的柔度 Cαz－Mz、随厚度t的增大而减小，当t＞1.5 mm时对柔度影响较小;分析图6可知:球铰的柔度 Cαz－Fy、Cy－Fy随l的增大而非线性增大，其中Cy－Fy变化最显著，Cαz－Mz和 Cαx－Mx随 l的增大而线性增大;从图7可知:球铰柔度随半径r增大而线性增大，但变化量不大。由分析可知，柔性铰链各设计参数对其转动柔度的影响程度依次为:厚度t影响最大，其次为长度l，再次是半径r，最后为材料弹性模量E。

4 结论

以上根据材料力学的知识推导了直梁型柔性球铰柔度计算公式，并利用有限元软件ANSYS进行了铰链柔度校核，结果表明:有限元和与解析公式结果偏差在16%以内，验证了理论解析公式的有效性。通过分析得知，柔性铰链各设计参数对其转动柔度的影响程度依次为:厚度t影响最大，其次为长度l，再次是半径r，最后为材料弹性模量E。为柔性铰链的工程设计提供了理论依据。

【1】左行勇，刘晓明．三种形状柔性铰链转动刚度的计算与分析［J］．仪器仪表学报，2006，27(12):1725 －1728．

【2】LOBONTIU N，GARCIA E．Analytical Model of Displacement Amplification and Stiffness Optimization for a Class of Flexure-based Compliant Mechanisms．Computer ＆ Stuctures，2003，81:2797 －2801．

【3】PAROS J M，WEISBORD L．How to Design Flexure Hinges［J］．Machine Design，1965，37(27):151 －156．

【4】吴鹰飞，周兆英．柔性铰链的设计计算［J］．工程力学，2002，19(6):136 －140．

【5】LOBONTIU N．Stiffness Characterization of Corner-filleted Flexure Hinges［J］．Review of Scientific Instruments，2004，75(11):4896 －4904．

【6】SMITH T S，BADAMI V G．Elliptical Flexure Hinges［J］．Review of Scientific Instruments，1997，68(3):1473 －1483．

【7】陈贵敏，刘小院．椭圆柔性铰链的柔度计算［J］．机械工程学报，2006，42(5):111 －115．

【8】曹锋，焦宗夏．双轴椭圆柔性铰链的设计计算［J］．工程力学，2007，24(4):178 －182．

【9】XU W，KING T G．Flexure Hinges for Piezo-actuator Displacement Amplifiers:Flexibility，Accuracy and Stress Considerations［J］．Precision Engineering，2002，19(1):4 －10．

【10】LOBONTIU N，PAINE J S N．Design of Circular Crosssection Corner-filleted Flexure Hinges for Three-dimensional Compliant Mechanisms［J］．Journal of Mechanical Design，2002，124(3):479 －484．

【11】侯文峰．双轴矩形截面角圆形柔性铰链回转精度分析［J］．机械工程学报，2010(9):15 －19．

【12】董为．基于大行程柔性铰链的6自由度并联机器人系统的研究［D］．哈尔滨:哈尔滨工业大学，2007:23－25．