平面2自由度并联机构动力学性能优化

高秀兰，鲁开讲，史革盟

(宝鸡文理学院，陕西宝鸡721007)

近年来，并联机器人的应用领域在不断扩大，随着科学技术的发展，对机构的性能提出了越来越高的要求。工作空间是机器人最重要的性能指标，合理地定义工作空间是机器人结构设计的首要环节。最大限度地提高机构的运动速度，是现代机器人技术发展的主要标志，为了适应高速和高加速度的要求，许多学者从运动学和动力学方面［1－8］提出了多种动态性能指标来量化机器人机构的动态性能。然而并联机构的工作空间与动态性能之间往往是矛盾的，为了获得良好的动态性能，只有放弃使用部分工作空间。目前并联机构的结构设计主要是基于运动学［9－12］和动力学［10－12］性能指标进行的，而兼顾机器人工作空间［13－15］的设计较少，其主要原因是并联机构工作空间的定义与描述本身就是一个难题。机构的工作空间与动态性能在很大程度上取决于机构的结构参数，对机构进行优化设计将是一种可行的方法，它可以兼顾工作空间和动态性能这两个方面，并使它们之间达到均衡，保证机构的总体性能最优。作者以关节驱动力矩在预定设计空间的最大值作为评定机构动力学性能的指标，将机构对设计空间的要求看作是对结构参数的约束，从而将机构的优化设计归结为约束优化问题，得到了兼顾设计空间和动力学性能的最优结构参数。

1 平面2自由度并联机构逆运动学分析

平面2自由度并联机构的末端点C通过两条支链与基座相连，如图1所示。取参考坐标系Oxy。

图1 平面2自由度并联机构运动简图

选取机构一个分支，构成开式运动链，该分支关节速度到动平台的运动速度˙x的映射关系

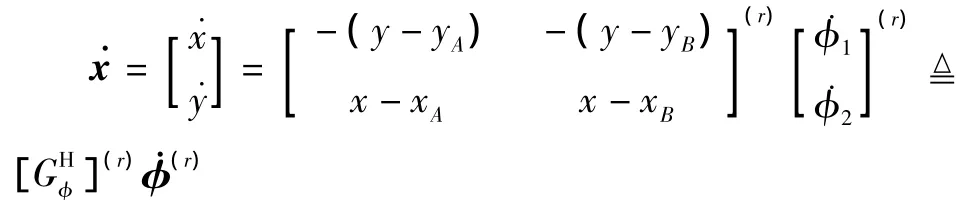
式中:x为末端点C的位置矢量，x=［x y］T，上标r表示分支序号，中的下标表示分支中运动副的序号。

当已知动平台的速度，可求得该分支关节相对速度

同样，可以得到每个分支关节运动加速度¨φ(r)到动平台的运动加速度矢量的映射关系

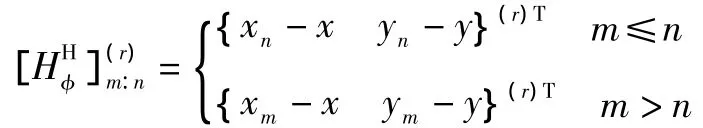
式中:xm、ym、xn、yn的下标与该分支关节序号对应。

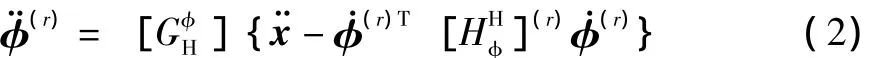
2 并联机构凯恩方程

2.1 输入构件广义主动力和广义惯性力计算

选取末端点C的坐标x、y为广义坐标。由式(1)得

输入杆质心Gr的速度

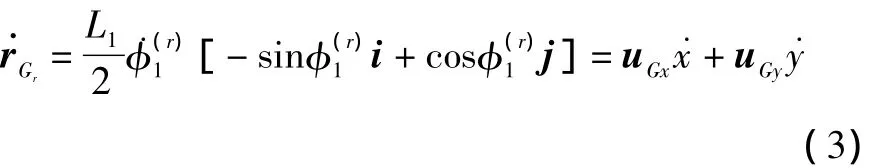
输入构件ArBr对各独立速度的偏角速度分别为

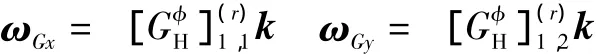
作用在输入构件上的主动力有重力及驱动力矩，取质心为简化中心，其主矢和主矩分别为

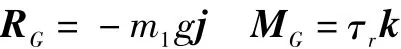
输入构件对各独立速度的广义主动力和广义惯性力

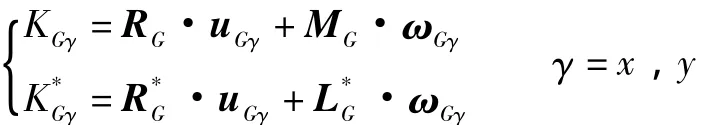
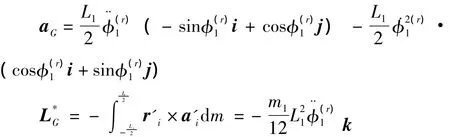
r'表示质量微元dm相对简化中心 (质心)的矢径，a'i为微元dm相对简化中心的加速度。

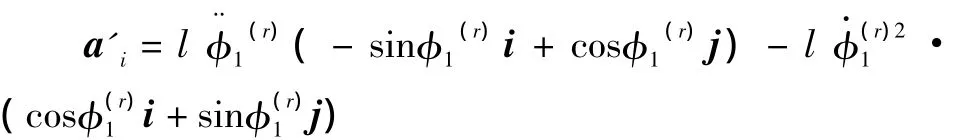
2.2 从动构件广义主动力和广义惯性力计算

由式 (1)得关节的相对角速度

从动构件角速度矢量

质心Q的速度

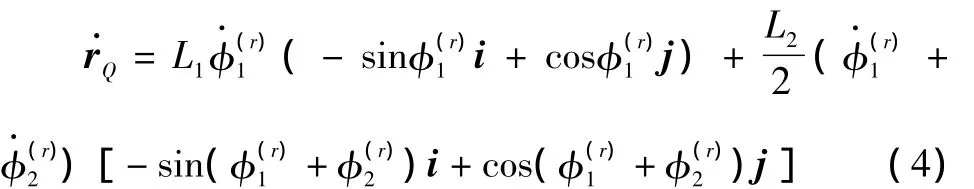
按独立速度整理

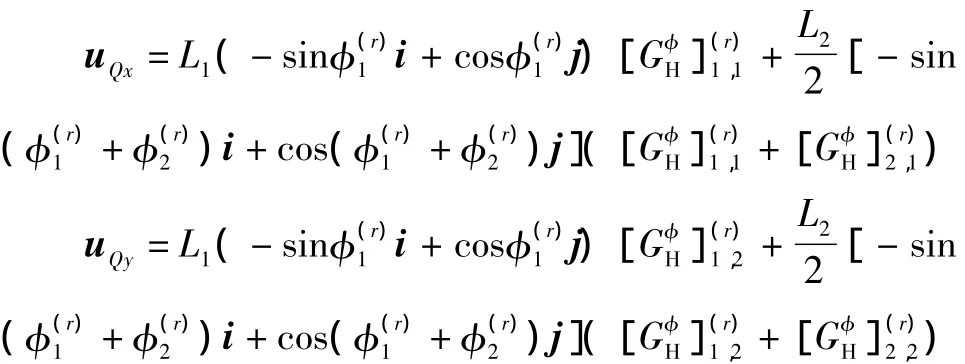
机构在末端点C处作用有集中力Fx和Fy(见图2)，它使得从动杆产生附加力，由于杆的重力比Fx和Fy要小得多，因而忽略杆的重力而将从动杆看作二力杆，认为从动杆对末端点的作用力沿杆轴线方向，对末端点进行静力分析求得附加力

图2 末端点C的受力分析

作用在从动构件上的主动力有重力和附加力。取质心为简化中心，其主矢和主矩分别为

从动构件对各独立速度的广义主动力和广义惯性力

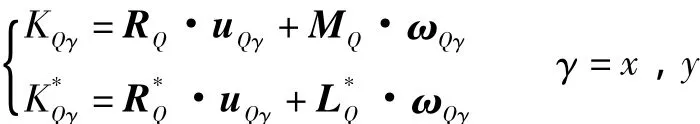
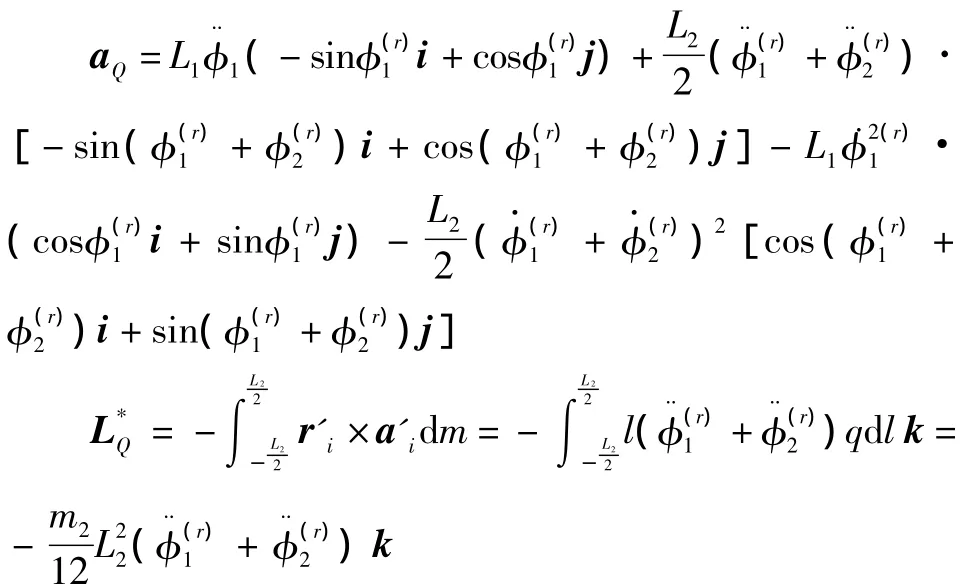
将所有构件上的广义主动力和广义惯性力分别求和，得到机构相对于各个独立速度广义主动力和广义惯性力

基于凯恩方法，可以得到机构的动力学方程

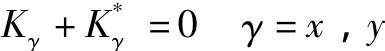
写成矩阵形式

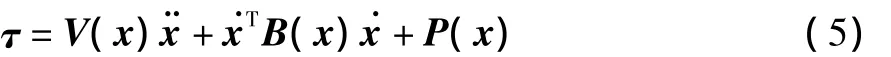
式中:τ为主动关节驱动力矩矢量，τ=［τ1τ2］T;

V(x)为操作空间的惯性矩阵，B(x)∈R2×2×2;

P(x)是克服外界负载和重力所需的关节驱动力矩，仅与机构的位形有关。

3 动力学性能优化

3.1 机构的工作空间与设计空间

机构每个分支的工作空间是以Ar为中心的环形区域，如图3所示，机构的工作空间是各支链子空间的交集，它由图中4段圆弧围成。如果要求工作空间能包容一个边长为b的正方形，中心在P(x0，y0)，其顶点为Ci

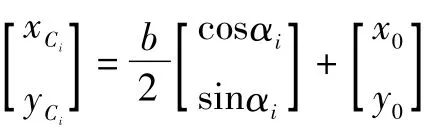
式中:αi为PiCi与x轴的夹角，α1，i=1～4。

图3 机构工作空间解析

如果给定设计空间，则机构结构尺寸必须满足下面的几何约束条件:

(1)过A1向C1C4引垂线，如果垂足 D1位于C1C4之间，则要求

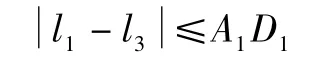
如果垂足位于C1C4之外，则要求

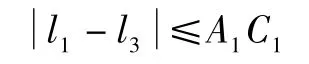
同样对于分支2，如果垂足位于C1C2之间，则要求

如果垂足位于C1C2之外，则要求

(2)在三角形A1G1A2中

(3)各支链子空间外边界应包含 C1、C2、C3、C4，即

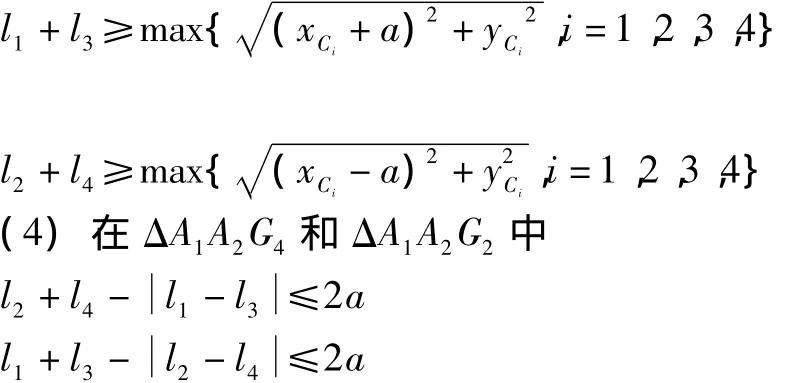
3.2 机构动力学性能指标和动力学优化设计

对机器人进行轨迹规划或实际控制时，必须考虑在整个设计空间以及机构运行速度和加速度的范围内，关节驱动力矩的最大值τmax

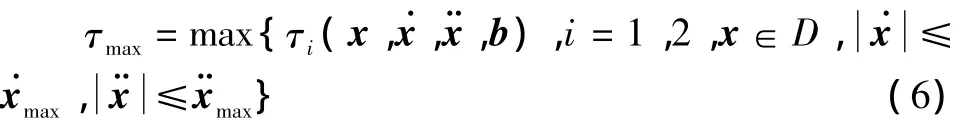
式中:b为设计变量，包括机构的结构参数和动力参数;i为分支序号;D为设计空间;、分别为允许运行的最大速度和加速度;τi为主动关节的驱动力矩。

τmax可以作为评定机构动力学品质优劣的性能指标，它代表机器人在整个工作空间的总体性能。

并联机构由多条分支组成，其工作空间是各分支子空间的交集，与传统的串联机器人相比，并联机构最大的不足就是工作空间相对较小。另外在工作空间中心部位，动力学性能良好，由里向外，机构的动力特性变差。为了获得良好的动力学性能，就要放弃使用靠近边界的这部分工作空间。对机构进行动力学优化设计，就是要兼顾设计空间与动力学性能这两个矛盾的方面，将机构对设计空间的要求看作是对结构尺寸的约束，从而将动力学优化描述成:给定机构的设计空间，确定一组结构参数和动力学参数，在结构参数满足工作空间要求的几何约束条件下，使机构的某种全局性能指标在整个设计空间最优。有实用意义的优化模型有:

(1)对于仅在低速运行的机构，为了使机构结构最紧凑，占用的空间最小，应使其结构尺寸的总和最小，即在结构尺寸满足第3.1节中的几何约束条件下，使

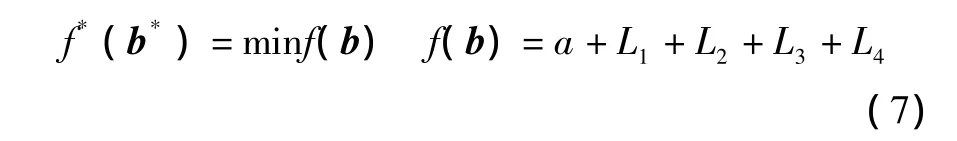
(2)对于加减速频繁和高速运行的机构，在结构尺寸满足第3.1节中的几何约束条件下，应使机构的动力性能最优，即

式 (6)的性能指标的含义是:在给定机构的结构参数和动力学参数以后，使机构的末端点以允许范围的速度和加速度在整个设计空间运行时，各个主动关节驱动力矩的最大值。

4 应用实例

根据使用要求，机构工作空间包含一个边长b=200 mm、中心坐标P(50 mm，300 mm)的正方形区域，将其视为机构预定的设计空间，并且要求机构工作时，末端点在此空间能达到的最大速度和加速度=(±2.5，±2.5)m/s，¨xmax=(±250，±250)m/s2。杆AB和BC为均质杆，直径分别为32 mm和25 mm。

让性能指标τmax分别取一系列指定值，可以得到关节驱动力矩在工作空间的等位线，如图4所示。可见:在工作空间的中部，关节驱动力矩小，机构动力学性能良好，由里向外，机构的动力学性能逐渐变差。如果将预定设计空间也表示在图中，将不难看出机构在设计空间中的最大驱动力矩。

图4 工作空间边界及关节驱动力矩等位线图

以机构结构参数为设计变量b=［L1，L2，L3，L4，a］，求解优化模型 (7)和 (8)，得到这两种情形下的最优结构参数，如表1所示。按尺度最优的设计方案绘制机构的工作空间，如图5所示，它与设计空间的关系表明，所得的结构参数是满足设计空间要求的最紧凑的构型要求。

表1 两种情形下的最优结构参数

图5 尺度最优方案下的工作空间与设计空间

为了测试优化结果对动力学性能影响的程度，用动力学仿真的方法，计算末端点在整个设计空间运动时的关节驱动力矩，结果如图6所示，关节驱动力矩在整个预定的设计空间峰值小，变化平缓，变化范围小。这预示着，按最优结构参数设计的机构，在预定的设计空间具有较好的动力学性能。

图6 动力性能优化后关节驱动力矩在设计空间的变化规律

5 结论

采用影响系数理论，分析了机构逆向运动学，以机构末端点坐标为广义坐标，建立机构动力学模型，关节驱动力矩能用解析式表示，为动力学性能的灵敏度分析创造了条件。将机构对设计空间的要求处理为对结构参数的几何约束，从而将机构的优化设计归结为基于性能指标的约束优化问题，所得的最优结构参数，兼顾了设计空间与动力学性能。在实例中，采用动力学仿真的方法，验证了方法的有效性。

【1】ASADA H．A Geometrical Represantation of Manipulator Dynamics and Its Application to Arm Design［J］．Trans of ASME J of Dynamic Systems，Measurement and Control，1983，105(3):131 －142．

【2】YOSHIKAWA J．Manipulability of Robotic Mechanisms［J］．Int J Robotics Research，1987，4(2):3 －9．

【3】刘爽，郭希娟，刘彬．4－RR(RR)R并联机构的动力学性能指标分析［J］．机械工程学报，2008，44(7):63－68．

【4】高洪，赵韩．6－3－3并联机构逆动力学分析与仿真［J］．农业机械学报，2007，38(9):130 －133．

【5】GUO Xijuan，CHANG F Q．Aceeleration and Dexterity Performance Indices for 6－DOF and Lower-mobility Parallel Mechanism［C］//ASME 2004 DETC，2004:851 －855．

【6】XU Younan，XI F F．A Real-time Method for Sowing the Forward Kinematics of a Tripod with Fixed-length Legs［J］．Journal of Manufacturing Science and Engineering，2006，128:1 －9．

【7】冯志友，张燕，杨廷力，等．基于牛顿欧拉法的2UPS－2RPS并联机构逆动力学分析［J］．农业机械学报，2009，40(4):193－197．

【8】郭希娟，彭艳敏，耿清甲．LR-Mate机器人动力学性能分析［J］．机械工程学报，2008，44(10):123 －128．

【9】刘新军，王立平，吴泽启，等．基于力传递性能的平面并联机器人的优化设计［J］．清华大学学报:自然科学版，2008，48(11):1926 －1930．

【10】MONSARRAT B，GOSSELIN C M．Workspace Analysis and Optimal Design of a 3－leg 6－DOF Parallel Platform Mechanism［J］．IEEE Transactions on Robotics and Automation，2003，19(6):954 －966．

【11】李宁宁，赵铁石．并联式四自由度定位平台性能优化［J］．机器人，2008，30(2):130 －137．

【12】郭祖华，陈五一，陈鼎昌．基于全局性能的并联机床结构参数优化［J］．中国机械工程，2004，15(20):861－864．

【13】彭斌彬，高峰．五轴并联机床的尺度综合［J］．机器人，2006，28(1):76 －80．

【14】曹永刚，张玉茹，马运忠．6－RSS型并联机构的工作空间分析与参数优化［J］．机械工程学报，2008，44(1):19－24．

【15】孙立宁，丁庆勇，刘新宇．2自由度高速高精度并联机器人的运动学优化设计［J］．机械工程学报，2005，41(7):94－98．