铝发热盘自动浇铸系统中平盘结构模态分析

弓满锋，隋广洲，梁炎锋

(湛江师范学院机电工程研究所，广东湛江524048)

发热盘是电饭锅的关键部件，随着社会经济发展，目前普通家庭基本上都用上了电饭锅，这也造成了目前电饭锅和电饭锅零部件市场需求巨大。目前尽管市场上电饭锅的种类繁多，功能强大，外形靓丽，但是其关键的部件发热盘却是手工浇铸出来的，这无疑不利于整个家电制造业产业水平的整体提升。文中研究的四工位发热盘自动浇铸系统可以极大地提高劳动生产率，提高操作安全性和降低劳动成本，提升家电制造业市场竞争力。鉴于铝发热盘自动浇铸系统各工位质量较大，平盘又时常处于旋转工作状态，并且浇铸的铝液温度高达500～600℃，故前期设计中对铝发热盘自动浇铸系统整体结构的安全性也提出了较高要求，设计中除了要考虑静力条件下结构的强度、刚度、稳定性以及疲劳等力学问题之外，也应考虑动力学问题。

模态分析是确定结构振动特性的一种技术［1］，如:确定结构的自然频率、振型、振型的参与系数。在结构动力学分析中，模态分析理论是基础，工程实践中，模态分析技术广泛应用于评价结构系统的动态特性、在新产品设计中进行结构动态特性的预估和优化设计、诊断及预报结构系统的故障、控制结构的辐射噪声、识别结构系统的载荷等［2］。作者在前期静力设计的基础上，通过模态分析技术研究四工位铝发热盘自动浇铸系统中平盘结构的固有频率和振型。

1 结构组成及工作原理

1.1 结构组成

铝加热盘整体浇铸系统大致可以分成以下几部分:(1)整体结构和工位结构的设计;(2)自动浇铸机器人子系统开发;(3)电气控制部分设计。这3个部分又以整体结构设计最为重要，该系统能否正常工作，整体结构设计是基础。为此，作者在设计阶段对发热盘自动浇铸系统整体结构进行模态分析，研究结构在自重和工位等效集中载荷作用下的固有频率和振型，以便更好地指导产品设计和制造。

1.2 工作原理

整个系统中有4个工位，其中A、B两个工位实现浇铸铝发热盘，C、D两个工位实现装卸铝发热盘，各工位逆时针方向低速旋转，依次实现各工序交接。因为各工位浇铸铝发热盘的原理是靠旋转离心浇铸，故各工位均有电机、传动部分、上模、下模、安全盖、出模等部件，每个工位部分的质量近于50～75 kg。这些载荷全部要靠浇铸平盘下的4个10号普通热压槽钢和用于支撑槽钢的4个三角形支撑板来承载。整体结构中主要承重部分是平盘、平盘下部槽钢、槽钢下部三角支撑板、套筒4个部件，且槽钢、三角支撑板、套筒相互间焊接，平盘和槽钢用标准紧固件连接。主要承重部件力学模型如图1所示。

图1 四工位铝发热盘自动浇铸系统力学模型

2 有限元 (FEM)分析

2.1 模态分析理论

用于模态分析的动力学有限元基本方程

式中:M为质量矩阵;C为阻尼矩阵;K为刚度矩阵;u为位移向量;F(t)为作用力向量;t为时间。若假定为自由振动，F(t)=0时，忽略阻尼的影响，则方程 (1)可简化为

若假定为简谐运动，模态分析的方程 (2)可转换为:

以上方程假定条件为:(1)模态分析假定结构是线性的 (如:MK保持为常数);(2)简谐运动方程，u=u0cos(ωt)，ω为自振圆周频率 (rad/s)。文中对铝发热盘自动浇铸系统中平盘结构进行的模态分析，即是在假定该结构处于简谐运动和线性条件下进行的，通过分析求出各阶特征值和特征向量，从而得到该结构各阶振动频率和振型。

2.2 有限元 (FEM)建模

整体坐标系统如图2中所示，材料均选用低碳钢，具体规格:选用10号槽钢，长1 350 mm，宽50 mm，厚5 mm;三角形支撑板形状为等腰直角三角形，两个直角边均为300 mm;圆形套筒外径270 mm，内径230 mm，长度310 mm;圆盘外径2 270 mm，内径270 mm，厚度2 mm。考虑到部分部件属于曲面连接，建立几何模型时，可先建立槽钢的体积模型V1，再建立三角形支撑板的体积模型V2，然后通过有限元中的布尔减运算减去一实心圆柱体V3(其原点在坐标原点，半径为135 mm、高度为310 mm)。这样就可将槽钢和三角形支撑板与套筒相接触的部位切成与圆形套筒外径135 mm相吻合的圆形，从而保证3个部件相接触的部位几何尺寸一致。为便于分析和计算，建立几何模型时适当忽略一些小的圆角、倒角、圆孔和凹槽等结构。

根据几何结构选用八节点六面体实体单元类型，在模态分析中采用SOLID 45单元［13］。在前处理过程中，对材料设置相应的材料常数和属性值，材料选HT250，密度 ρ=7 800 kg/m3，弹性模量 E=207 GPa，泊松比0.3。考虑到平盘和槽钢是紧固件连接，故需将两者相接触的所有面积设置成接触面，这一步骤需在划分网格后进行。文中是考虑有预应力作用的旋转平盘模态分析问题，施加的预应力来自两个方面:(1)外载荷，故在平盘x、y轴正负方向上分别施加4个等效的集中载荷 (加载点位于整体坐标系中xOy面上，且离坐标原点832 mm处)，大小为1 kN;(2)结构自重的影响，故还需在z轴负方向施加9.8 m/s2的重力加速度。对结构施加绕z轴旋转的角速度ω=10 rad/s。对自动浇铸系统四臂结构采用SOLID 45进行四面体自由划分网格，为保证计算精度，将模型分别以单位20，30，50，70 mm进行网格划分，采用4种网格划分后的有限元模型分别如图2中 (a)、(b)、(c)、(d)所示。

图2 4种网格划分有限元模型

2.3 计算精度分析

对自动浇铸系统四臂结构套筒内表面进行全约束，计算得到4种网格划分状况下该结构的前10阶固有频率，如表1所示。

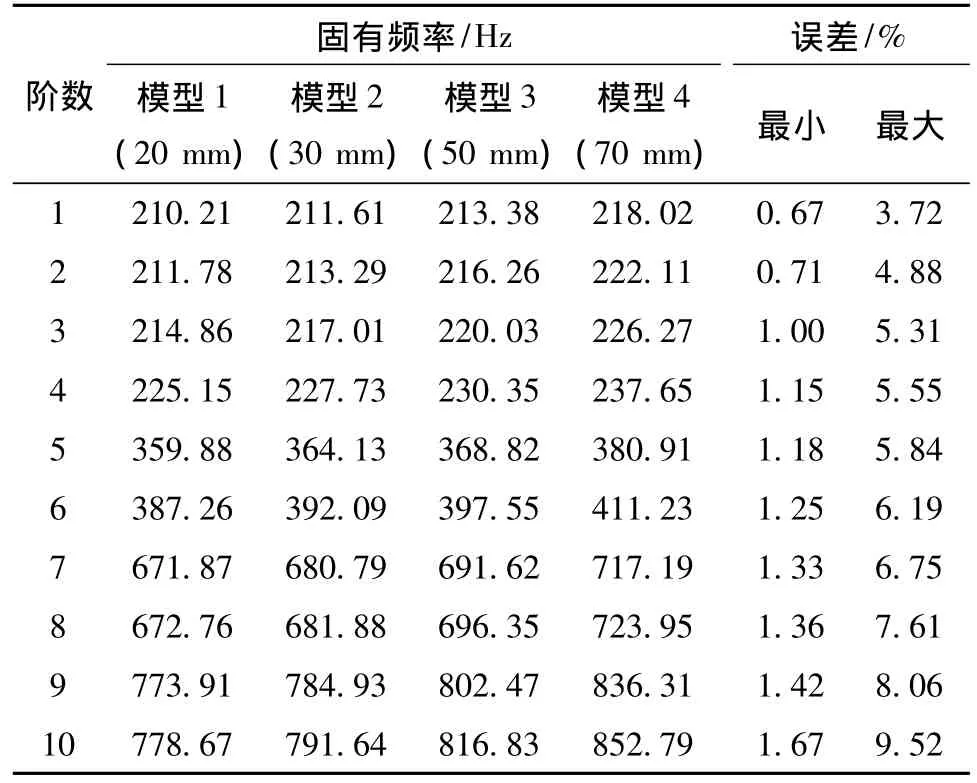
表1 4种网格划分时该结构的前10阶固有频率

依据有限元理论，随着网格密度加大，单元数急剧增加，计算时间和计算量加大，但是计算结果也将收敛于精确解［3］。表1中的网格划分单元长度成倍递减，可以看出计算精度明显提高，如模型4与模型1之间的误差较大，最大达到9.52%，这主要是模型4单元划分较为粗糙，从而影响计算结果的精度;而模型2与模型1之间的误差却很小，最大仅为1.67%，因此可知模型1的结果已经足够精确。文中有限元分析即采用20 mm单元长度的自由网格划分技术来实施计算。后面讨论的计算结果也对应于20 mm单元长度的自由网格划分有限元模型，采用BLOCK LANCZOS法对该结构进行有预应力的模态分析。

3 结果讨论与分析

模态分析1～6阶振型结果如图3所示，由图(a)、(b)可知:该结构第1阶振型表现为平盘绕z轴的小角度转动，平盘并无明显的弯曲和伸缩变形，振动频率210.21 Hz。由图 (c)、(d)可知:该结构第2振型表现为平盘绕xy平面内平分二四象限的直线弯曲变形，平盘并无绕z轴扭转和径向伸缩变形，振动频率211.78 Hz。由图 (e)、(f)可知:该结构第3阶振型表现为平盘绕xy平面内平分一三象限的直线弯曲变形，平盘无绕z轴扭转和径向伸缩变形，振动频率214.86 Hz。由图 (g)、(h)可知:该结构第4阶振型表现为平盘向z轴正向的弯曲变形，平盘无绕z轴扭转和径向伸缩变形，振动频率225.12 Hz。由图 (i)、(j)可知:该结构第5阶振型表现为平盘向z轴负向的弯曲变形，平盘无绕z轴扭转和径向伸缩变形，振动频率359.88 Hz。由图 (k)、 (l)可知:该结构第6阶振型表现为平盘绕x和y轴的扭转变形，平盘无明显的绕z轴扭转和径向伸缩变形，振动频率387.26 Hz。该结构前3阶的固有频率比较接近，振型也较为常见，该结构属于低速转动，故4～6阶的振型较为少见，而后面的7～10阶的结构振动固有频率远超过该结构允许的最大工作状态了，其振型相比于前3阶固有频率更为少见，所以7阶后的固有频率和振型就不作分析讨论了。1—6阶四工位结构自动浇铸系统的固有频率及振型见表2。

对于文中分析的四工位铝发热盘自动浇铸系统中平盘结构，由于其转速较低，所以可忽略结构产生噪声的问题，但是要严格控制该结构旋转时的变形过大问题，显然文中讨论的平盘结构旋转时弯曲变形较大，而且最大弯曲变形均出现在平盘最大直径轮缘位置，这对结构的安全性、寿命和机器人浇铸、拆装产品操作等都带来不利的影响。可以通过以下的具体措施予以解决:(1)减小平盘直径。平盘直径的减小将有助于提高结构稳定性和减小弯曲变形;(2)通过在平盘轮缘下加装旋转支撑装置，在旋转时自下而上对平盘轮缘进行支撑，这对于减小弯曲变形和提高槽钢强度均有利;(3)减轻浇铸工位的质量，文中讨论时是在4个工位分别施加了1 kN的等效集中力，换算成质量为100 kg，这样重的工位质量显然对旋转平盘造成过大的弯曲变形，倘若速度提高，则弯曲变形程度将更为严重，故应考虑使用轻质、设计科学有效的工位工装夹具，以便提高整体结构的刚度。

图3 模态分析结果

表2 四工位结构自动浇铸系统的固有频率及振型

4 结论

尽管四工位发热盘自动浇铸系统的整体结构工作时属于低速旋转，但是倘若平盘z向承载较重，将导致结构刚度不足，平盘出现较大的弯曲变形。为了克服这个问题，可以通过以下措施予以解决。

(1)减小平盘直径。平盘直径的减小将有助于提高结构稳定性和减小弯曲变形。

(2)在平盘轮缘下加装自下而上旋转支撑装置，这对于减小弯曲变形和提高槽钢强度均有利。

(3)减轻浇铸工位的质量，应考虑使用轻质、设计科学有效的工位工装夹具，以便提高整体结构的刚度。

【1】李卫民，杨红义，王宏祥．ANSYS工程结构实用案例分析［M］．北京:化学工业出版社，2007:222－246．

【2】李连峰，高栋梁，隋秀伟，等．修井机盘式制动器模态分析［J］．石油矿场机械，2011，40(3):59 －62．

【3】李书明，黄燕晓，程关兵．航空发动机涡轮盘固有模态分析［J］．中国民航大学学报，2008，26(2):8 －11．