基于回归设计技术的平面磨削表面粗糙度研究

池龙珠

(江苏技术师范学院，江苏常州213001)

磨削技术是机械制造业中实现精密加工最有效、应用最广的制造技术。表面粗糙度作为磨削表面质量的重要参数之一，直接影响零件的使用性能。由于磨削过程极其复杂，影响加工表面粗糙度的因素众多，而且各因素之间的各种物理、化学现象伴随于整个磨削过程，所以对磨削技术的理论研究和实践应用都存在很大难度，大大限制了磨削加工的科学管理及生产效益的提高。纵观已有的有关表面粗糙度的研究，诸如形成机制及预测方法等，多为金属刀具的切削［1－2］，而没有多少关于砂轮磨削表面粗糙度的研究［3－4］。作者利用试验设计技术及回归设计技术，对平面磨削表面粗糙度进行了研究，提出表面粗糙度的预测模型，同时给出利用这个模型控制表面粗糙度、优化磨削条件的方法，以期对表面粗糙度的预测与控制、合理选择磨削参数提供可资利用的依据。

1 实验设备、测试方法

实验选用如下设备与装备:SGH-600平面磨床(Nakase，Japan)，SJ-210P表面粗糙度测量仪 (Mitutoyo)，WA40(120，200)LmVA225×20×50.8砂轮，工件材料为SKH51高速钢 (HRC62，100×90×20 mm)。每次实验前，以单颗粒金刚石对砂轮进行修正，以尽可能减少实验误差。表面粗糙度测试方法如图1所示。每次实验均测量工件两端和中间共3点的表面粗糙度，然后取其平均值作为当次实验的表面粗糙度值。

图1 表面粗糙度测试方法示意图

2 试验设计、试验数据及分析

2.1 试验设计及试验数据

众所周知，影响磨削表面粗糙度的因素有很多。选取砂轮转速、工件速度、磨削深度、砂轮粒度等4个因素为主要影响因素，每一因素再各取3个水平，如表1所示。然后利用标准正交表L27(313)进行平面磨削实验。表2为根据所采用的L27(313)正交表配列的每一试验号的因素、水平以及试验数据。

表1 试验因素、水平选取表因

表2 正交试验设计及试验结果

2.2 试验数据分析

图2所示为根据试验号排列的表面粗糙度的试验结果。

图2 按着试验号排列的表面粗糙度试验值

从图2可以看出表面粗糙度并没按着试验号顺序呈现一定的增加或减小的规律性。这正是正交实验的优点，是由于在每次试验时，同时改变多个因素的水平所引起的，充分体现正交表的均衡分布思想。

图3所示为各因素的不同水平下表面粗糙度的分布规律图，图中表示了表面粗糙度的最小、最大、中间值、平均值及25%至75%的分布区间。

图3 表面粗糙度分布规律图

从图3可以看出砂轮粒度号为200#(D2)和砂轮转速为2 100 r/min(A2)时，可以获得较小和较稳定的表面粗糙度。

3 表面粗糙度回归分析

3.1 表面粗糙度回归模型的建立

各独立因素对试验指标的反应结果，可以用线性回归设计和非线性回归设计进行预测。线性回归设计虽然能简化计算，但只能回归出线性方程，而在实际情况下，必须考虑因素的二次或更高次的作用。因此还必须进行非线性回归设计。通常进行二次回归设计就可以满足一般非线性问题的基本要求。由于磨削用量对磨削表面粗糙度的影响不呈现单调线性关系，所以也采用二次回归设计。通用的二次回归设计模型［5］如下:

根据公式 (1)，表面粗糙度Ra与各因素之间的二次回归模型可以用公式 (2)表示。

其中系数矩阵β可以用公式 (3)计算。

在式 (3)中，X代表由实验条件所构成的矩阵(27×15)，Y代表由实验结果所构成的矩阵 (27×1)。将表2所给出的实验条件和实验结果代入式(3)，便能得到系数矩阵β(15×1)，再将所得β代入式 (2)，即可得到下面的二次回归方程。

3.2 回归模型的显著性检验

为了验证回归模型的显著性，采用F检验法进行检验，其结果如表3所示。

表3 回归模型显著性检验表

表中各项平方和用公式 (5)计算［6］。为了直观地了解回归模型的回归效果，把实验值与预测值进行了对比，其结果如图4所示。

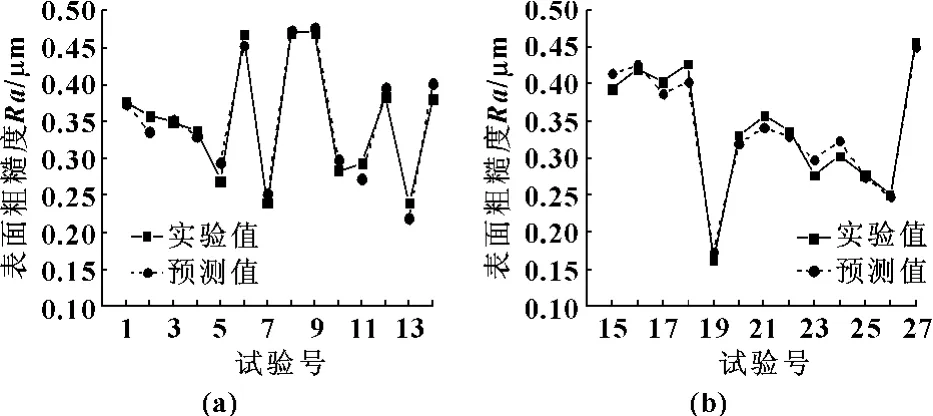
图4 预测值与实验值

从表3的检验结果及图4可知回归方程的回归效果是良好的。

3.3 回归模型的决定系数

评价回归模型精度，除了上述的F检验之外，也可以用决定系数来评价，记为r2，即

决定系数r2反映了因变量的变异中能用自变量解释的比例。其数值在0～1之间。决定系数r2越接近1，说明因变量不确定性的绝大部分能用回归方程解释，回归方程的拟合度好［7］。把表3的相关数据代入公式 (8)即可得出决定系数，即

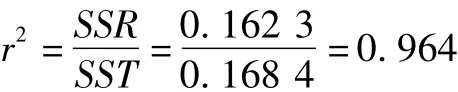
为了更直观地表达其拟合效果，把实验值与预测值的对应分散结果用图5表示。

图5 实验值与预测值的对应分散结果

由决定系数r2及图5可以看出回归方程的拟合度是良好的。

3.4 实验验证

为了进一步验证回归效果，选择没在表2实验范围内的任意4个实验条件(A1B0C0D2)，(A1B2C1D0)，(A1B1C0D1)，(A2B0C2D1)进行了实验，同时利用回归方程进行预测，其比较结果如图6所示。从图可以看出回归模型的预测效果是良好的。

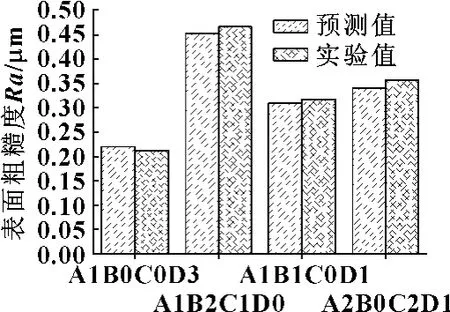
图6 实验值与预测值比较

3.5 利用预测模型的表面粗糙度控制与预测

图7所示为当砂轮转速为1 500 r/min、砂轮粒度为40#时，根据回归方程 (4)绘制的反映磨削深度和工件速度对表面粗糙度影响规律的表面粗糙度三维图。从图中可以很直观地看出表面粗糙度随磨削深度和工件速度变化的规律。

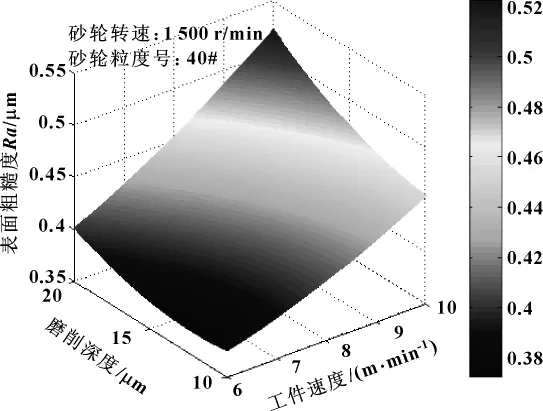
图7 表面粗糙度三维图

图8所示为表面粗糙度二维等值线图。利用表面粗糙度二维等值线图可以很方便地对表面粗糙度进行预测和控制。例如当磨削深度为16 μm;工件速度为7 m/min时，表面粗糙度为0.4 μm。若当磨削深度为15 μm时，要想控制表面粗糙度为0.4 μm以下，则工件速度应控制在7.2 m/min以下。

图8 表面粗糙度二维等值线图

如图9所示在表面粗糙度二维等值线图上附加单位时间金属切除量MMR曲线，就可以很方便地确定最优参数组合，寻找适宜的工艺条件。单位时间内的金属切除量MMR可以用下式进行计算。

式中:C代表磨削深度 (μm);B代表工件速度(m/min);b代表砂轮的宽度 (mm，这里取值20 mm)。

由图9可知，点a与点b的金属切除量相同，但点b的表面粗糙度低于点a。因此，若选择点b代表的磨削深度和工件速度，即可在保证金属切除量相同的前提下获得更低的表面粗糙度;点a与点c具有相同的表面粗糙度，但点c的金属切除量大于点a。所以，若选择点c代表的磨削深度和工件速度，便可在保证表面粗糙度相同的前提下获得更大的金属切除量。

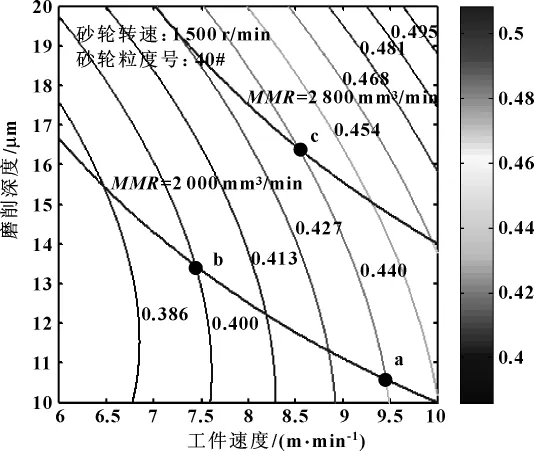
图9 表面粗糙度二维等值线与单位时间金属切除率

4 结论

采用标准正交表进行4因素3水平的平面磨削试验，并用回归设计技术建立了表面粗糙度二次回归预测模型，并对回归预测模型进行了F检验和决定系数r2检验。结果，F0=23.2＞F0.01(14，12)=4.04，r2=0.964，这表明所建立的回归预测模型达到显著水平，回归预测方程具有良好的拟合度。由所建立的二次回归预测模型，可获得表面粗糙度二维等值线图，能直观地反映表面粗糙度与金属切除量、磨削用量的关系。这为表面粗糙度的预测与控制，同时选择合理的磨削参数提供了有价值的参考依据，是一种简便有效的方法。

【1】石文天，刘玉德，丁悦，等．PCD刀具微细车削硬铝合金的表面质量研究［J］．机床与液压，2011，39(17):15－17．

【2】杨济森，郭宏伟，李洪涛．航空铝7050高速铣削表面粗糙度试验研究［J］．机械制造与自动化，2011，40(3):34－35．

【3】李国发，王龙山，丁宁．基于进化神经网络外圆纵向磨削表面粗糙度的在线预测［J］．中国机械工程，2005，16(3):223－226．

【4】许峰，谢勇，单世远，等．基于Matlab图像处理的磨削表面粗糙度的检验［J］．工具技术，2011，45(10):83 －84．

【5】任露泉．回归设计及其优化［M］．北京:科学出版社，2009．

【6】朴聖炫．應用實驗計畫法［M］．首尔:民英社，1990．

【7】何晓群，刘文卿．应用回归分析［M］．北京:中国人民大学出版社，2011．