时间步长及网格尺度对物质输运数值模拟结果的影响

曹 刚

（山西省水利水电勘测设计研究院，山西 太原 030024）

1 引言

随着我国经济的迅猛发展，水环境受到各方面的普遍重视。在此背景下，随着环境水力学数值模拟技术及计算机水平的进步，水动力—物质输运数学模型以其经济性好、所受限制少、信息完整、便于修改保存以及能够满足实际工作需求等优势，在环境影响评价、水资源保护、水利工程风险评估、水环境容量分析等方面得到越来越广泛的应用。从数值模拟的角度而言，水环境数值模拟结果的精度及可靠性与计算采用的时间步长和网格尺度关系密切。文章依托国内外普遍认可的国际通用软件，对给定的计算方案采用不同的时间步长及网格尺度进行多组次的平行数值实验，通过对数值模拟结果的分类对比分析，研究了时间步长及空间网格尺度对数值模拟结果的影响。

下文以长10 000 m、宽100 m的平底矩形断面明渠为对象，上游给定流量边界200 m3/s，下游给定水位边界（水深5 m），渠道中部偏上游位置投放保守物质作为示踪剂，投放时间30 s，以此模仿河道中有限时间排放源排放的物理过程。数值模拟组次包括不同时间步长（变幅0.0~0.5 min）以及不同网格尺度（30 m×10 m，15 m×10 m，7.5 m×5 m）的多种组合工况。

2 数学模型

2.1 初始条件

本文研究初始条件采用冷启动，即给定初始水位，各流速分量初始值设定为0，初始保守物质浓度为0，计算一定时间，待流场稳定后，再按照设定浓度模拟投放保守物质30 s。

2.2 控制方程的离散及求解

该模型的数值求解采用有限差分法对正交曲线坐标下的平面二维水动力连续方程、运动方程及物质输运方程进行离散，得到离散的控制方程，再对其采用交替方向隐式法（ADI）及迭代法进行数值求解。

3 数值模拟结果及分析

3.1 不同时间步长计算结果比较

表1给出了在网格尺度30 m×10 m时，不同时间步长条件下，保守物质投放后渠道内峰值浓度的变化过程。数据分析可知，保守物质投放后，随水流逐渐向下游推移，在水体对流稀释和扩散作用下，示踪剂的峰值浓度随时间推移逐渐下降。

表1 30 m×10 m网格尺度时不同时间步长的峰值浓度

本文还分别对15 m×10 m，7.5 m×5 m网格时，不同时间步长条件下，保守物质投放后渠道内峰值浓度的变化过程进行了数值模拟。计算结果表明，各种网格尺度下，渠道内示踪剂的峰值浓度变化过程表现出一致的规律性，仅在保守物质投放初期，不同网格尺度下的峰值浓度之间存在一定差值，并有时间步长越小、峰值浓度越大的趋势，但实际数据数值相差极为有限，随着时间的推移，各组数据很快趋于一致。且各时间步长下峰值浓度变化的相位也保持一致。这一结果表明，此类数值模拟任务在保证计算稳定性的前提下，计算结果对时间步长不敏感。

3.2 不同网格尺度计算结果比较

表2给出了时间步长为0.01 min时不同网格尺度下，保守物质投放后渠道内峰值浓度的变化过程。由表2中数据可见，保守物质投放后，随水流逐渐向下游推移，在对流稀释和扩散作用下，峰值浓度逐渐下降。

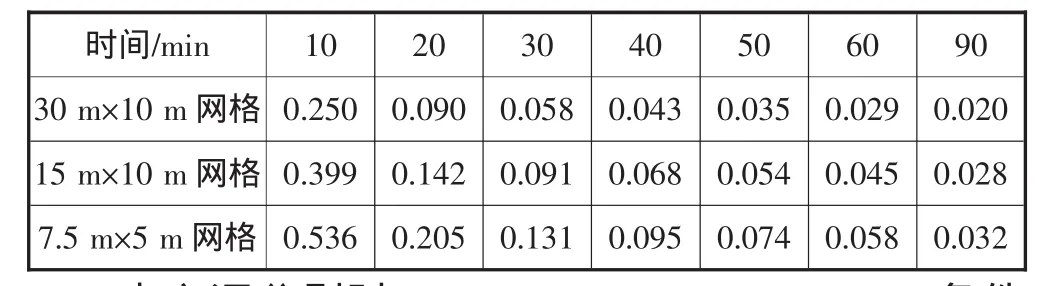
表2 时间步长0.01 min时不同网格尺度下峰值浓度变化

本文还分别对 0.05 min，0.10 min，0.25 min条件下，不同网格尺度条件下，保守物质投放后渠道内峰值浓度的变化过程进行了分析研究。研究结果表明，在0.05 min，0.10 min，0.25 min时间步长下，渠道内保守物质峰值浓度变化过程规律性一致，且这一规律与不同时间步长下结果一致。在保守物质投放初期，不同网格尺度下峰值浓度之间存在明显差值，并呈现网格尺度越小、峰值浓度越大的趋势，峰值浓度变化的相位也有微小差别。随着时间的推移，各组数据逐渐趋于重合，但其差别远较不同时间步长下情况明显。计算结果表明，在此类数值模拟中，网格尺度对计算结果的影响局限在一定的区域内，但其影响程度与范围远较时间步长变化的作用明显。

4 结论

本文采用二维平面水动力—传质数学模型模拟了明渠有限时间排放源的情况下，保守物质在水流中的输运过程，计算了不同时间步长及网格尺度情况下保守物质的浓度分布变化情况，得到了多组次的平行计算结果。

数值模拟结果表明，保守物质投放后，随水流逐渐向下游推移，在对流稀释和扩散作用下，峰值浓度逐渐下降。在不同的时间步长下，仅在保守物质投放初期，峰值浓度之间存在微小差值，峰值浓度变化的相位保持一致，随着时间的推移，各组数据很快趋于重合，表明此类数值模拟任务在保证计算稳定性的前提下，计算结果对时间步长不敏感。

在保守物质投放初期，不同网格尺度下峰值浓度之间存在明显差值，并呈现网格尺度越小、峰值浓度越大的趋势，峰值浓度变化的相位也有微小差别。随着时间的推移，各组数据逐渐趋于重合，表明在此类数值模拟中网格尺度对计算结果的影响局限在一定的区域内，但其影响程度与范围远较时间步长变化的作用明显。进一步分析数值模拟过程可知，导致计算结果在一定范围内对网格尺度敏感性较高的原因在于，模型计算中，将一个时间步长内投放的保守物质在一个网格单元中进行瞬间稀释，时间步长相同时，单元越小，初始浓度越高，故初始阶段的峰值浓度也随之升高。但数值模拟结果表明，这种影响仅在有限的时间与空间尺度上发生作用，对远区无明显影响，远区结果已属于网格无关解。

因此，对网格尺度应根据所作研究的具体需要进行选择，若关心物质排放点附近的分布情况，则应加密网格，当网格数量已不满足数值模拟的经济性和可实现性要求时，应考虑采用其他研究方法。