粘弹性夹层圆板自由振动的理论解*

廖明建 李映辉

(1．西南交通大学力学与工程学院，成都 6 10031)(2．中国工程物理研究院总体工程研究所，绵阳 6 21900)

粘弹性夹层圆板自由振动的理论解*

廖明建1，2†李映辉1

(1．西南交通大学力学与工程学院，成都 6 10031)(2．中国工程物理研究院总体工程研究所，绵阳 6 21900)

研究了粘弹性夹层圆板的自由振动特性．基于经典弹性薄板理论和Kelvin－Voigt粘弹性本构方程，建立了粘弹性夹层圆板振动控制方程．采用分离变量法导出了粘弹性夹层圆板的自然频率及振型解析表达式，计算了固支和简支粘弹性夹层圆板的自然频率，并与有限元计算结果进行比较;讨论了粘弹性夹层圆板的夹心层比率对自然频率及衰减系数的影响．研究表明:(1)随着夹心层厚度的增大，系统频率先增大后减小，高阶时该趋势表现更为明显;(2)随着夹心层厚度的增大，衰减系数一直增大，高阶时该趋势表现更为明显．

粘弹性夹层圆板， 自由振动， Kelvin－Voigt， 分离变量法

引言

粘弹性夹层板结构通常由刚度较大的上下约束层和阻尼较大的粘弹性中间层构成．由于其具有质量轻、强度高、刚度大，减振效果明显等诸多优点，已广泛应用于航空、航天、船舶等重要工业中．因此，研究粘弹性夹层板结构的动力特性尤为重要，尤其是研究自由振动特性．但目前对自由振动特性的研究主要集中在梁、矩形板、圆形膜、圆形板和圆柱壳等结构［1－12］．文献［1］研究了粘弹性地基上弹性梁的自由振动特性;文献［2］研究了轴向运动梁在纵向与横向振动耦合下的自由振动特性;文献［3］和文献［4］研究了矩形薄板在四边固支情况时自由振动;文献［5］研究了四边简支条件下正交各向异性蜂窝夹层矩形板的固有特性;文献［6］研究了粘弹性基础上矩形薄板振动的基本理论与计算方法;文献［7］研究了圆形薄膜的固有频率及其振型的理论求解方法;文献［8］研究了弹性地基上圆形薄板的有阻尼振动问题，给出了计算固有频率的计算公式;文献［9］讨论了求解Kelvin模型粘弹性基础上圆形薄板自由振动固有频率的方法;文献［10］研究了两端简支功能梯度薄壁圆柱壳的自由振动特性．对于粘弹性夹层圆板结构的自由振动特性研究还很少见到．

本文拟基于经典弹性薄板理论和Kelvin－Voigt粘弹性本构方程，建立粘弹性夹层圆板的振动控制方程，采用分离变量法导出粘弹性夹层圆板的自然频率及振型的理论解，计算固支和简支粘弹性夹层圆板的自然频率，通过与有限元计算进行比较，说明方法的正确性．在此基础上，进一步讨论夹层圆板厚度对自然频率及衰减系数的影响．

1 控制方程

1．1 粘弹性夹层圆板模型

图1为粘弹性夹层圆板模型，上下两层为对称约束层，中间夹心层为Kelvin－Voigt微分本构粘弹性材料．约束层弹性模量 Ec，泊松比μc，密度 ρc，厚度 h /2;夹心层弹性模量 Ej，泊松比 μj，密度 ρj，厚度H，粘弹性阻尼系数η，粘弹性夹层板等效密度ρ=(ρch+ρjH)/(H +h)．

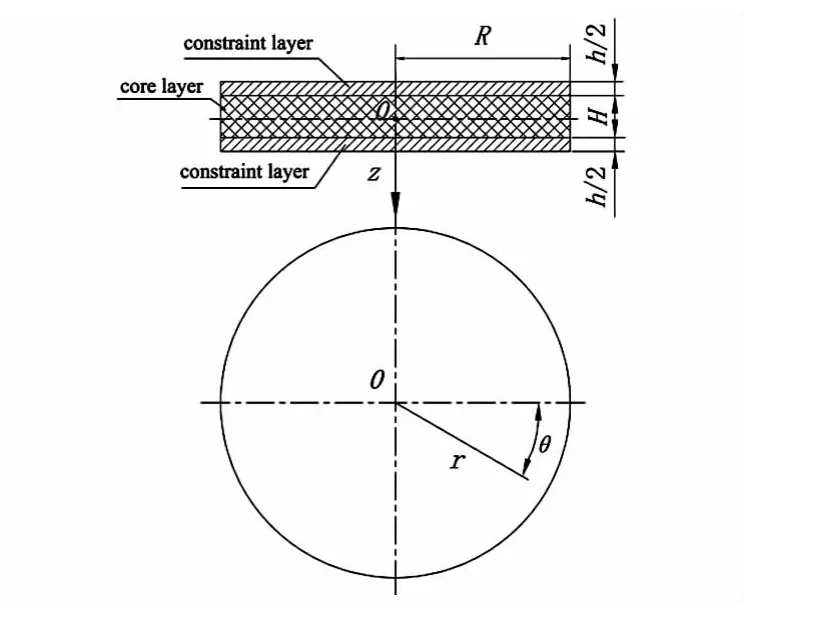
图1 粘弹性夹层圆板模型Fig．1 Model of viscoelastic circular plate

1．2 粘弹性夹层圆板控制方程

假定夹层圆板处于小挠度状态，忽略面内力影响．由于圆板的形状关系，采用圆柱坐标系来研究问题较直角坐标系更方便．将静平衡时中面的圆心O作为坐标原点(见图1)，z为通过圆心O且垂直于中面的方向坐标，r为中面上的点距z轴的距离．在柱坐标系下，粘弹性夹层圆板的平衡方程为

其中，Qr、Qθ、Mr、Mθ、Mrθ分别为径向剪力、切向剪力，径向弯矩、切向弯矩和扭矩，w为板中面位移，q为横向荷载．

板内任意一点径向位移u和切向位移v分别为

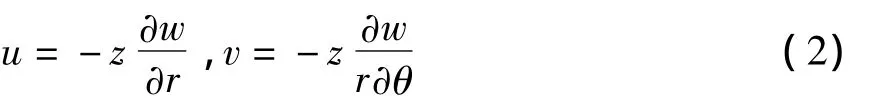
夹层板应变与挠度w关系为

约束层应力与应变关系为

夹心层应力与应变关系为

夹层板的弯矩和扭矩分别为

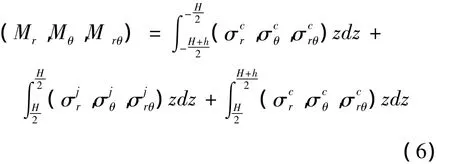
将(3)代入(4)和(5)，将(4)和(5)代入(6)，再将(6)代入平衡方程(1)，得粘弹性夹层圆板的振动方程为

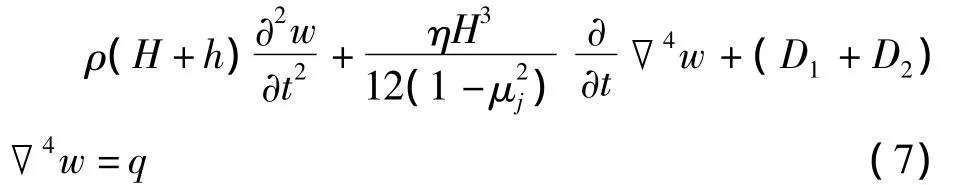
其中，D1、D2、▽4表达式分别为

2 对粘弹性夹层圆板振动方程的讨论

2．1 弹性板

当夹心层厚度H=0时，方程(7)退化为

当粘弹性阻尼系数η=0，且夹心层和约束层的弹性模量和泊松比均一致时，方程(7)退化为

式(9)和(10)为经典弹性薄圆板的横向振动方程［13］．

当粘弹性阻尼系数η=0，但夹心层和约束层弹性模量和泊松比不一致时，方程(7)退化为不同材料组成的夹层薄圆板振动方程

2．2 粘弹性板

当约束层厚度h=0时，方程(7)退化为粘弹性薄圆板的横向振动方程:

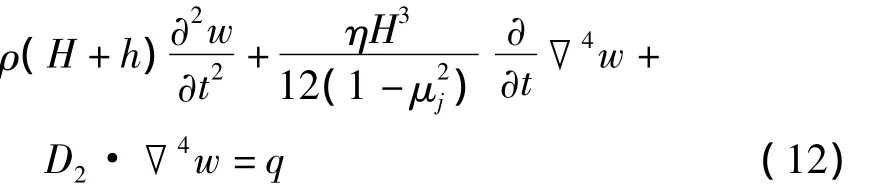
由上述分析可知，方程(7)是包含了弹性薄圆板(单层或夹层)和粘弹性薄圆板横向振动的统一方程，具有通用性．

3 粘弹性夹层圆板振动特性

3．1 粘弹性夹层圆板固有振型

若方程(7)中q=0，即得粘弹性夹层圆板自由振动基本方程．采用分离变量求解，令

将式(13)代入方程(7)，可导出变量分离的微分方程

其中，ω为待求的常数．令

则(14a)可分解为

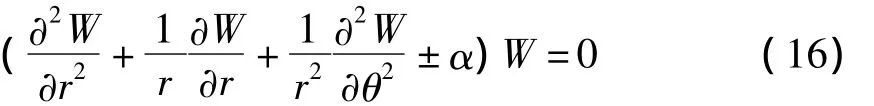
对方程(16)再次采用分离变量法，令

把式(17)代入方程(16)，得到微分方程

分离变量后得

其中m为待求的常数．式(19a)为二阶常系数微分方程，其解为

式(19b)为Bessel(贝塞尔)方程，其解为

其中 Jm(αr)、Nm(αr)、Im(αr)、Km(αr)分别为实宗量的第一类及第二类贝塞尔函数、虚宗量的第一类及第二类贝塞尔函数．

于是，式(17)的通解为

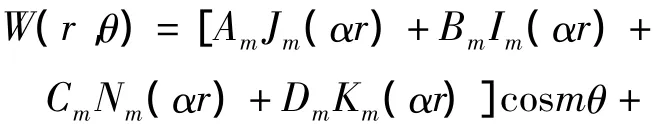
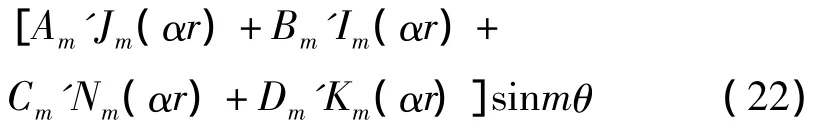
对于完整的夹层圆板，在圆心(r=0)处W应为有限值，但由于 Nm(αr)、Km(αr)在圆心时无穷大，所以必须有Cm=Dm=C'm=D'm=0．若夹层圆板的边界条件以某轴对称，则将θ=0坐标轴放在该轴上，必有以 θ=0轴对称振型，所以可以取sinmθ项系数A'm=B'm=0．因此粘弹性夹层圆板固有振型表达式为

其中系数Am和Bm由圆板的边界条件确定．

3．2 周边固支粘弹性圆板的自然频率

周边固支夹层圆板的边界条件为

将式(23)代入(24)得

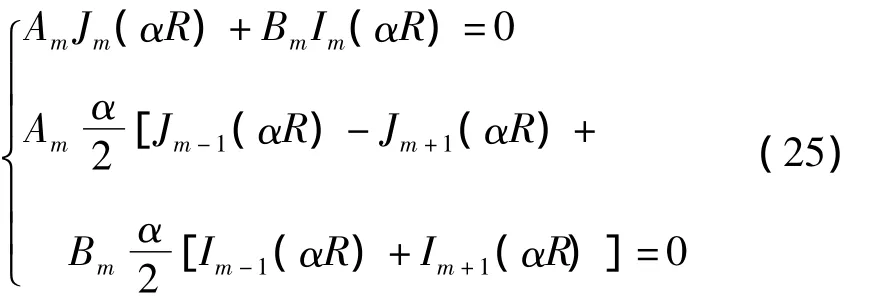
式(25)为关于 Am、Bm的线性代数方程组，由于Am、Bm不恒等于零，则系数行列式为零，得频率方程为

记频率方程(26)的第n个正根为αmnR，则固支粘弹性夹层圆板的固有振型为

对每一个αmnR值，均可由式(15)确定 ωmn．每个ωmn对应一个Tmn(t)方程，即式(14b)

其中，ζmn的表达式为

当小阻尼情况，即＜1时，可得方程(28)解为

式(31a)、(31b)分别是固支粘弹性夹层圆板自由振动频率和衰减系数的表达式．

3．3 周边简支粘弹性圆板的自然频率

周边简支夹层圆板的边界为

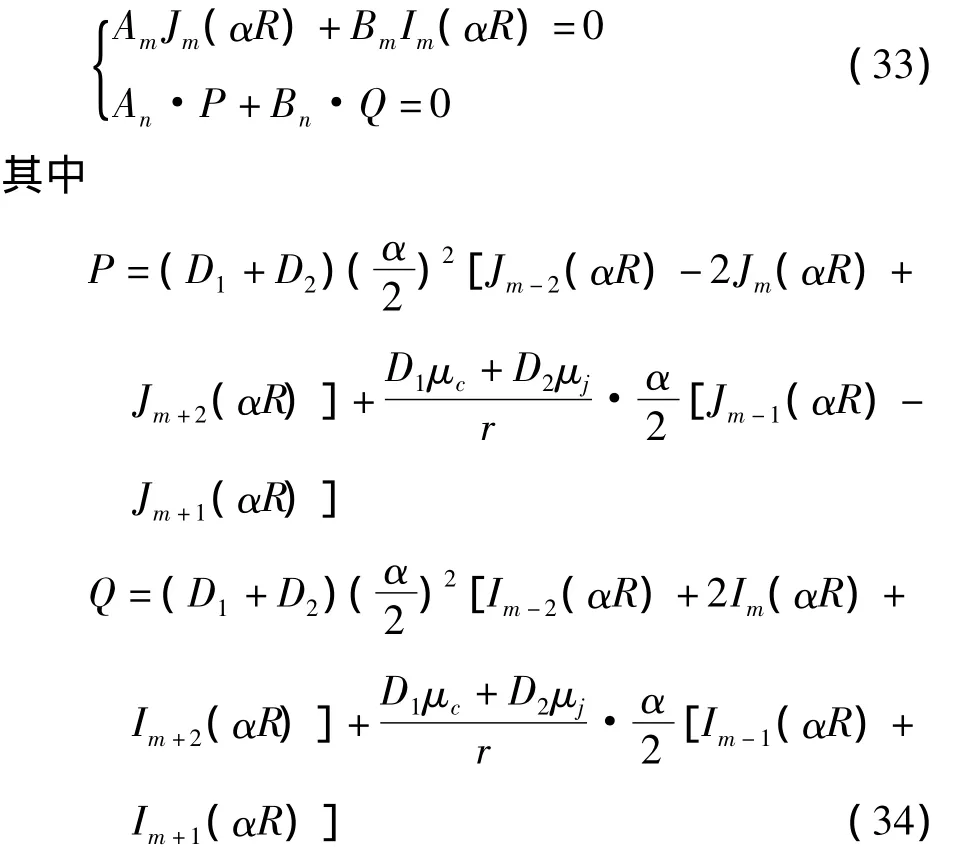
将式(23)和(6)代入式(32)得

式(33)为关于Am、Bm的线性代数方程组，由于Am、Bm不恒等于零，则系数行列式为零，得频率方程为

为便于与频率方程(26)的正根αmnR有所区分，将频率方程(35)的第n个正根记为βmnR，则简支粘弹性夹层圆板的固有振型为

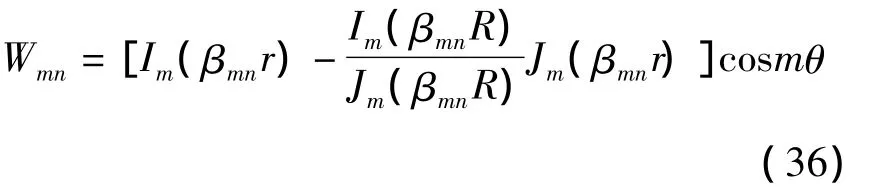
对每一个βmnR值，同理可由式(15)先确定ωmn，再由式(31)求出简支粘弹性夹层圆板频率和衰减系数．

4 算例

4．1 理论解的有效性验证

本算例中粘弹性夹层圆板的几何尺寸和材料参数数值见表1．

表1 粘弹性夹层圆板的几何尺寸和材料参数Table 1 Table 1 Geometry size and material parameters of the viscoelastic sandwich circular plate

表2、表3分别给出了固支和简支粘弹性夹层圆板各阶自然频率及其对应固有振型的理论计算结果，并与有限元(FEM)结果进行了比较．表中m为节径数，n为节圆数．从表2和表3可见，理论解与有限元结果比较接近，表明本文计算方法有效．

表2 边固支粘弹性夹层圆板自然频率(Hz)Table 2 Natural frequency(Hz)of fixed sandwich circular plate

表3 周边简支粘弹性夹层圆板自然频率Table 3 Natural frequency(Hz)of of simply supported sandwich circular plate

4．2 夹心层比率对频率的影响

夹心层比率定义为夹心层厚度占夹层板总厚度的比值．图2、图3分别给出了半径1．0 m、总厚度0．012 m固支和简支粘弹性夹层圆板各阶频率随夹心层比率的变化．算例中材料参数见表1．图中m为节径数，n为节圆数．从图2和图3可见，固支和简支粘弹性夹层圆板各阶频率随夹心层比率的变化趋势相同，均表现出随夹心层比率增大，先缓慢增大，到峰值后减小的趋势;高阶时表现更为明显．

图2 固支夹层板的夹心层比率对频率的影响Fig．2 The effect of the core ratio on the frequency of fixed sandwich circular plate

图3 简支夹层板的夹心层比率对频率的影响Fig．3 The effect of the core ratio on the frequency of simply supported sandwich circular plate

4．3 夹心层比率对衰减系数的影响

图4、图 5分别给出了半径 1．0 m、总厚度0．012 m的粘弹性夹层板衰减系数随夹心层比率的变化．算例中材料参数见表1．图中m为节径数，n为节圆数．从图4和图5可见，衰减系数均表现出随夹心层比率增大，呈上升趋势;高阶时衰减系数趋势表现更为明显．

图4 固支夹心层比率对衰减系数的影响Fig．4 The effect of the core ratio on the damping coefficient of fixed sandwich circular plate

图5 简支夹心层比率对衰减系数的影响Fig．5 The effect of the core ratio on the damping coefficient of simply supported sandwich circular plate

5 结论

根据经典弹性薄板理论，建立了粘弹性夹层圆板振动控制方程，采用分离变量法求得粘弹性夹层圆板的自然频率解析表达式，计算了周边固支和简支粘弹性夹层圆板的自然频率，与有限元结果进行比较，验证了本文方法的有效性．这一理论结果对以后研究粘弹性夹层圆板强迫振动的动力响应具有重要意义，也可用于验证其它方法数值解的正确性．同时，研究了粘弹性夹层圆板自然频率及衰减系数随夹心层比率的关系．得到如下结论:夹心层比率增大，结构频率先缓慢增大，到峰值后减小，高阶时表现更为明显;夹心层比率增大，结构衰减系数不断增大，高阶时表现更为明显．

本文推导出求解粘弹性夹层圆板自由振动理论解的方法可以推广到求解弹性支承边界、固支与简支混合边界等更多情况下的粘弹性夹层圆板自然频率和振型．这时，只需更换为相应的边界条件．

1 刘学山，冯紫良，胥兵．粘弹性地基上弹性梁的自由振动分析．上海力学，1999，20(4):470～475(Liu X S，Feng Z L，Xu B．Free vibration analysis for elastic beam on viscoelastic foundation．Shanghai Journal of Mechanics，1999，20(4):470 ～475(in Chiniese))

2 黄建亮，陈树辉．纵横向耦合轴向运动梁的自由振动响应研究．动力学与控制学报，2010，8(4):316～321(Huang J S，Chen S H．Study on vibration of an axially moving beam with coupled transverse and longitudinal motions．Journal of Dynamics and Control，2010，8(4):316～321(in Chiniese))

3 张强．矩形薄板四边固支时的自由振动分析．铁道建筑，2010，8:142 ～ 144(Zhang Q．Free vibration analysis for the fixed supported rectangular plate．Railway Engineering，2010，8:142 ～144(in Chiniese))

4 钟阳，张永山．四边固支弹性矩形薄板的自由振动．动力学与控制学报，2005，3(2):66～70(Zhong Y，Zhang Y S．Free vibration of rectangular plate with completed clamped supported．Journal of Dynamics and Control，2005，3(2):66 ～70(in Chiniese))

5 王盛春，邓兆祥，沈卫东等．四边简支条件下正交各向异性蜂窝夹层板的固有特性分析．振动与冲击，2012，31(9):73～77(Wang S C，Deng Z X，Shen W D，Wang P，Cao Y Q．Connatural characteristics analysis of rectangular orthotropic honeycomb sandwich pannels with all edges simply supported．Journal of Vibration and Shock，2012，31(9):73～77(in Chiniese))

6 张系斌．粘弹性地基上矩形薄板的振动．工程力学，2000，(增刊):248～252(Zhang X B．Vibration of the rectangular thin plates on viscoelastic foundation．Engineering Mechanics，2000，(supplement):248 ～252(in Chiniese))

7 林文静，陈树辉，李森．圆形薄膜自由振动的理论解．振动与冲击，2009，28(5):84～86(Lin W J，Chen S H，Li S．Analytical solution of the free vibration of circular membrane．Journal of Vibration and Shock，2009，28(5):84～86(in Chiniese))

8 解英艳，宋力，赵丹耀．圆形薄板的阻尼振动问题．沈阳工业学院学报，1995，14(1):81～86(Xie Y Y，Song L，Zhao D Y．Solutions to the damped vibration of circular thin plate on the elastic base．Journal of Shenyang Institute of Technology，1995，14(1):81～86(in Chiniese))

9 张系斌．粘弹性地基上圆形薄板的振动．工程力学，2001(增刊):805～808(Zhang X B．Vibration of the circular thin plates on viscoelastic foundation．Engineering Mechanics，2001(supplement):805 ～ 8 08(in Chiniese))

10 杜长城，李映辉．功能梯度薄壁圆柱壳的自由振动．动力学与控制学报，2010，8(3):219 ～223(Du C C，Li Y Y．Free vibration of functionally graded cylindrical thin shells．Journal of Dynamics and Control，2010，8(3):219～223(in Chiniese))

11 崔灿，李映辉．变截面铁木辛柯梁振动特性快速计算方法．动力学与控制学报，2012，10(3):258～262(Cui C，Li Y H．A solution for vibration characteristic of Timoshenko beam with variable cross－section．Journal of Dynamics and Control，2012，10(3):258 ～ 2 62(in Chinese))

12 蒋宝坤，李映辉，李亮．旋转粘弹性夹层梁非线性自由振动特性研究．动力学与控制学报，2013，11(3):241～245(Jiang B K，Li Y H，Li L．Vibration analysis of rotating viscoelastic sandwich beam．Journal of Dynamics and Control，2013，11(3):241 ～245(in Chinese))

13 徐芝纶．弹性力学．北京:高等教育出版社，2006(Xu Z L．Elastic mechanics．Beijing:Higher Education Press，2006(in Chinese))

*The project supported by the National Natural Science Foundation of China(11072204)，the Fundamental Research Funds for the Central Universities(SWJTU11ZT15)and the Key Program for Science and Technological Development Funds of China Academy of Engineering Physics(2010A0203007)

† Corresponding author E－mail:zhaoliaofei2005@yahoo．cn

ANALYTICAL SOLUTION OF THE FREE VIBRATION OF VISCOELASTIC SANDWICH CIRCULAR PLATE*

Liao Mingjian1，2†Li Yinghui1
(1．School of Mechanics and Engineering，Southwest Jiaotong University，Chengdu610031，China)(2．Institute of Systems Engineering，China Academy of Engineering Physics，Mianyang621900，China)

Free vibration characteristics of viscoelastic sandwich circular plate is presented．Based on the basic assumption of elastic thin plate and Kelvin－Viogt constitutive equation，the vibration control equation of the viscoelastic circular plate is established．The analytical expression of natural frequency and modes of free vibration is derived by employing the method of separated variables．The natural frequency of fixed and simply supported sandwich circular plate are calculated respectively．The results are compared with finite element method．The influence of core ratio on natural frequency and damping coefficient is discussed．Conclusions are as follows:(1)The natural frequency increases at first，then decreases with the increase of core ratio．It is more obvious for high order frequency．(2)The damping coefficient always increases with the increase of core ratio．

viscoelastic sandwich circular plate， free vibration， Kelvin－Voigt， method of separated variables

31 July 2012，

29 August 2012．

10．6052/1672－6553－2013－040

2012－07－31 收到第 1 稿，2012－08－29 收到修改稿．

*国家自然科学基金(11072204)、中央高校业务费专项(SWJTU11ZT15)、中国工程物理研究院科学技术发展基金重点资助项目(2010A0203007)

E－mail:zhaoliaofei2005@yahoo．cn