用Timoshenko修正理论研究有梯度界面层双材料梁的振动特性*
吴晓 罗佑新 黄 翀 杨 立军
(湖南文理学院,常德 4 15000)
用Timoshenko修正理论研究有梯度界面层双材料梁的振动特性*
吴晓†罗佑新 黄 翀 杨 立军
(湖南文理学院,常德 4 15000)
采用Timoshenko梁修正理论研究了有梯度界面层双材料梁的振动问题,利用静力方程确定了有梯度界面层双材料梁的中性轴位置,在此基础上应用Timoshenko梁修正理论建立了有梯度界面层双材料梁的振动方程,求得其自振频率表达式及其在简谐荷载作用下强迫振动的解析解.讨论分析了梯度界面层高度等因素对有梯度界面层双材料梁的振动影响,并用有限元法验证了Timoshenko梁修正理论.通过实例计算,得到了梯度界面层高度等因素对有梯度界面层双材料梁振动特性有较大影响的结论.
Timoshenko梁, 梯度界面层, 中性轴, 振动
引言
功能梯度材料是基于一种全新的材料设计概念合成的新型复合材料[1-11],日本科学家于二十世纪八十年代末年提出了功能梯度材料的概念以来,在航空航天、材料、汽车、电子等领域得到了越来越广泛的应用.功能梯度材料根据具体的要求,选择使用两种不同性能的材料,通过连续平滑地改变两种材料的组织和结构,使其结合部位的界面消失,从而得到功能相应于组织变化而变化的均质材料,最终减小或消除结合部位的性能不匹配因素.现工程实际中又出现了以功能梯度材料为夹芯的有梯度界面层的夹芯板梁结构,即在涂层和基层之间增加一层功能梯度材料粘结层以降低热应力和层间应力、提高抗冲击能力[12].基于上述原因,本文研究了弹性模量沿梁高呈线性变化的梯度界面层各向同性双材料梁的振动问题,并讨论分析了有关因素对有梯度界面层双材料梁振动特性的影响.
1 振动微分方程
有梯度界面层双材料梁的模型如图1所示,上下层分别为不同的均质材料,中间界面层为功能梯度材料.上层的弹性模量、密度分别为E1、ρ1,中间界面层的弹性模量、密度分别为 E2(z)、ρ2(z),下层的弹性模量、密度分别为E3、ρ3.

图1 有梯度界面层双材料梁Fig.1 Bi-material cantilever beam with graded interface layer
假设坐标原点建立在有梯度界面层双材料梁的中性轴上,中间层功能梯度材料的弹性模量、剪切模量、密度取任意函数的麦克劳林级数展开项中的0次和1次项,即:

根据Timoshenko梁修正理论假设φ为梁截面弯曲转角,y为梁的挠度,可知有梯度界面层双材料梁的应力表达式为:

有梯度界面层双材料梁弯曲时横截面内力应满足下式


式中z0为梁中性轴与下层底边之间的距离.
把式(1)、式(2)代入式(3)中可以得到

利用式(2)可得有梯度界面层双材料梁的弯矩、剪力表达式为

式中,k为剪切因子,

对于图1所示在横向动荷载作用下的有梯度界面层双材料梁,参阅文献[13-17]可知采用Timoshenko梁修正理论得到振动微分方程为


把式(5)、式(6)代入式(7)中可以得到
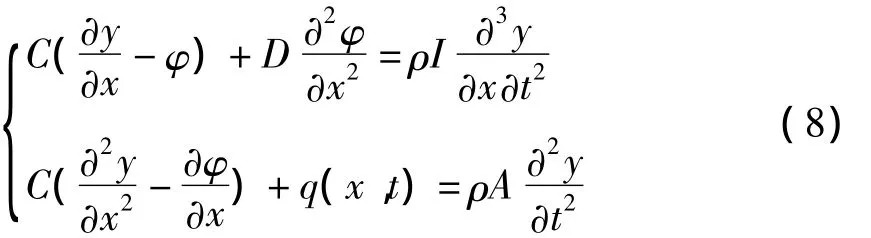
把式(8)解耦后可得修正Timoshenko梁振动方程为

2 有梯度界面层双材料梁振动解
2.1 自由振动的解
令有梯度界面层双材料梁的自由振动位移及外载荷分别为

把式(10)代入式(9)中可以得到

由式(11)可以求得有梯度界面层双材料梁振型函数为
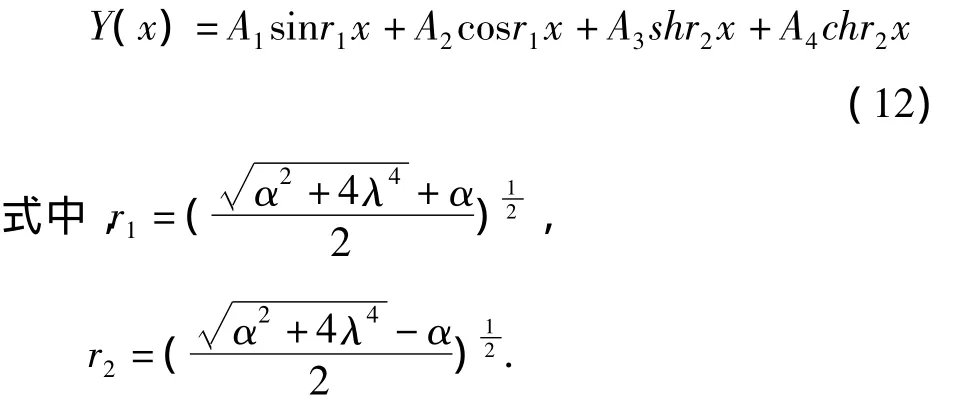
以简支梁为例,可知有梯度界面层双材料梁的边界条件为
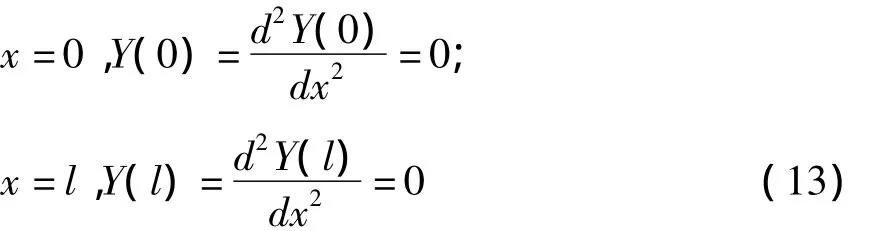
利用式(12)、式(13)可以求得有梯度界面层双材料梁的自振频率为

所以,有梯度界面层双材料梁的振动位移为
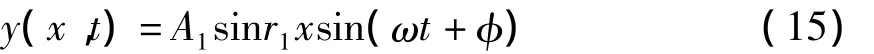
2.2 强迫振动的解
为了研究有梯度界面层双材料梁的强迫振动,可令式(9)解为:
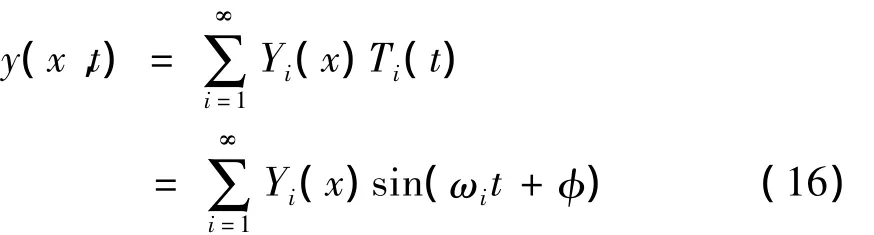
假设式(11)在简支梁的边界条件下,对应于ωi和ωj的两个振型函数为 Yi(x)和 Yj(x),把式(16)代入式(11)中,于是有
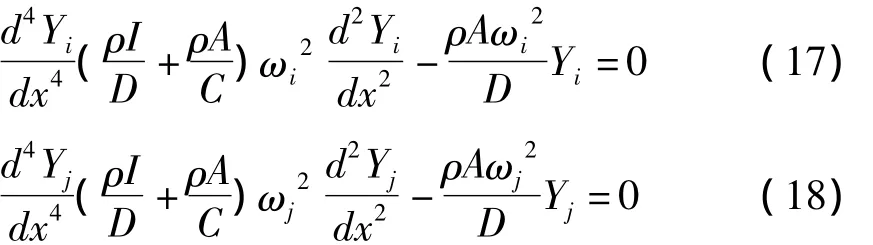
将式(17)乘以 Yj(x)、式(18)乘以 Yi(x),然后把所得的两个乘式相减,再沿梁全长积分,注意在积分式中代入铰支座边界条件,即得所需要的正交性方程式l

把式(16)及简支梁振型函数代入式(9)中并应用式(19)可以得到

假设分布荷载q(x,t)在时间上与空间上可分离,可令

把式(21)代入式(20)中积分可得

设功能梯度材料梁的初始条件为

由式(23)可以确定
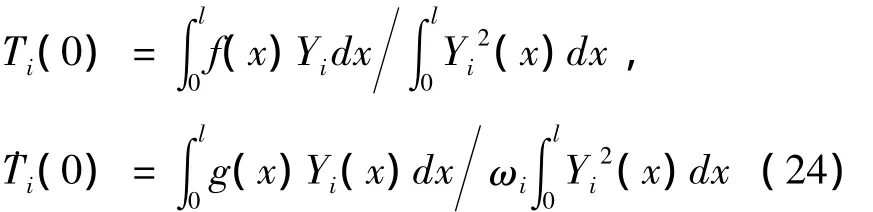
若作用在梁上的外扰力为沿梁长为均匀分布的简谐干扰力,利用式(22)可以求得

若在简支梁x=l0处作用有一简谐干扰力P0sinΩt,则有 q(x,t)=P0δ(x - l0)sinΩt,利用式(22)可以得到
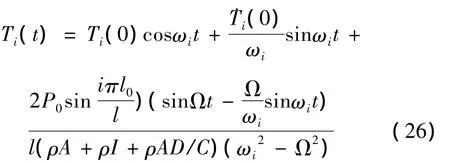
3 算例分析及讨论
为了分析有简支有梯度界面层双材料梁的动力特性,取梁长



表1 简支有梯度界面层双材料梁固有频率Table 1 Natural frequency of simply supported bi-material cantilever beam with graded interface layer
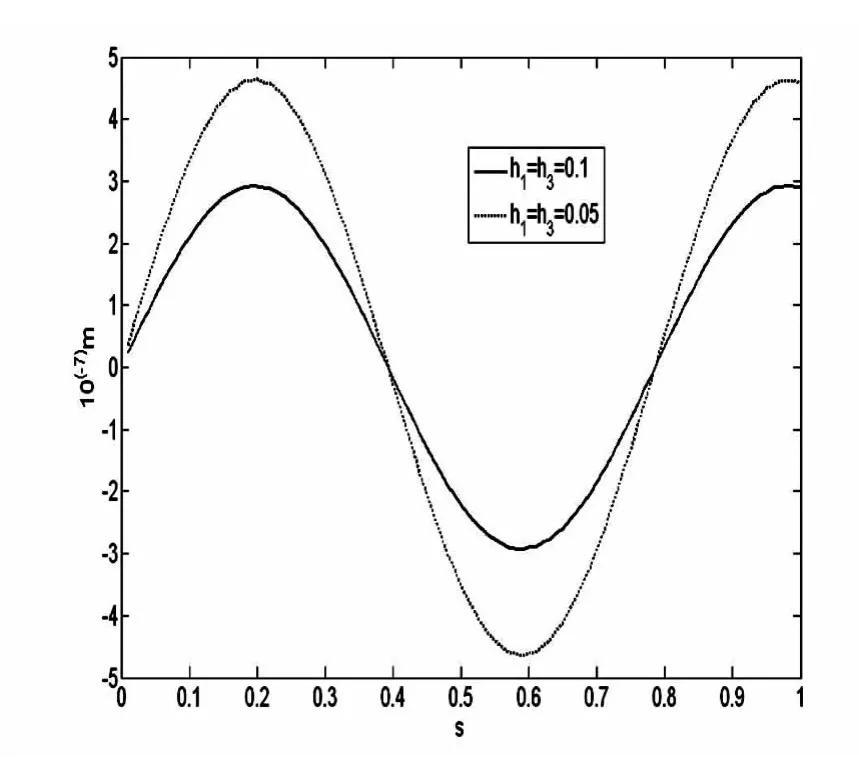
图2 梁中点动力响应曲线(q0=1000 N/m)Fig.2 The dynamic response curve of the beam midpoint

图3 梁中点动力响应曲线(P0=1000 N)Fig.3 The dynamic response curve of the beam midpoint
由表1可以知道:采用Timoshenko梁修正理论计算的有梯度界面层双材料梁固有频率与有限元法计算的有梯度界面层双材料梁固有频率非常接近,且随着固有频率阶数的的增加,Timoshenko梁修正理论计算结果与有限元法计算结果的误差也在增大,但是都没超过工程所允许的误差.这说明采用Timoshenko梁修正理论计算有梯度界面层双材料梁的固有频率还是比较合理的.
对表1进行分析可以看出,随着有梯度界面层双材料梁中间梯度层的高度增加,有梯度界面层双材料梁的固有频率将减小;这说明中间梯度层的高度增加将使有梯度界面层双材料梁的刚度降低.而且中间梯度层的高度变化对梁固有频率增减的影响还是较大的,尤其是对有梯度界面层双材料梁低阶固有频率的影响是非常明显的.
对图2、图3还可知道,随着有梯度界面层双材料梁中间梯度层的高度增加,有梯度界面层双材料梁在外激励载荷作用下,梁中点动力响应曲线的振幅将增大.原因是中间梯度层的高度增加将使有梯度界面层双材料梁的刚度降低,这样就导致了梁中点动力响应曲线的振幅的增大.集中载荷外激励作用在有梯度界面层双材料梁中点时的动力响应曲线振幅要大于均布载荷外激励作用在有梯度界面层双材料梁中点时的动力响应曲线振幅.
4 结论
由以上分析可以得到以下结论:
1)采用Timoshenko梁修正理论计算梁的固有频率是比较合理的.
2)随着有梯度界面层双材料梁中间梯度层的高度增加,有梯度界面层双材料梁的固有频率将减小,有梯度界面层双材料梁在外激励载荷作用下梁中点动力响应曲线的振幅将增大.
3)集中载荷外激励作用在有梯度界面层双材料梁中点时的动力响应曲线振幅要大于均布载荷外激励作用在有梯度界面层双材料梁中点时的动力响应曲线振幅.
1 吴晓,黄翀,杨立军,等.功能梯度材料圆板的非线性热振动及屈曲.动力学与控制学报,2012,10(1):52~57(Wu X,Huang C,Yang L J,et al.Nonlinear thermal vibration and buckling of functionally graded circular plate.Journal of Dynamics and control,2012,10(1):52 ~ 5 7(in Chinese))
2 Zhong Z,Yu T.Vibration of a simply supported functionally graded piezoelectric rectangular plate.Smart Materials and Structures,2006,15:1404~1412
3 Zhong Z,Shang E T.Three-dimensional exact analysis of a simply supported functionally gradient piezoelectric plate.International Journal of Solids and Structures,2003,40(20):5335~5352
4 尚尔涛,仲政.功能梯度热释电材料平板柱形弯曲问题的精确解.应用力学学报,2003,20(4):122~125(Shang E T,Zhou Z.Exact solutions for functionally graded piezothermoelectric plates in cylindrical bending.Chinese Journal of Applied Mechanics,2003,20(4):122 ~125(in Chinese))
5 Chen W Q,Ding H J.On free vibration of a functionally graded piezoelectric plates.Acta Mechanica,2002,153 ~207
6 Wu X H,Chen C Q,Shen Y P,et al.A high order theory for functionally graded piezoelectric shells.International Journal of Solids and Structures,2002,39(20):5325 ~5344
7 王铁军,马连生,石朝锋.功能梯度中厚圆/环板轴对称弯曲问题的解析解.力学学报,2004,36(3):348~353(Wang T J,Ma L S,Shi Z F.Analytical solutions for axisymmetric bending of functionally graded circular/annular plates.Acta Mechanica Sinica,2004,36(3):348 ~353(in Chinese))
8 马连生,赵永刚,杨静宁.功能梯度圆板的轴对称非线性分析-大挠度问题.兰州理工大学学报,2004,30(6):139 ~ 142(Ma L S,Zhao Y G,Yang J N.Axisymmmtric nonlinear analysis of functionally graded circular plate:large deflection bending problem.JournalofLanzhou University of Technology,2004,30(6):139 ~142(in Chinese))
9 马连生,赵永刚,杨静宁.径向压力作用下功能梯度圆板的过屈曲.兰州理工大学学报,2006,32(4)::158~161(Ma L S,Zhao Y G,Yang J N.Post~buckling of a functionally graded circular plate subjected to radial compression.Journal of Lanzhou University of Technology,2006,32(4):158~161(in Chinese))
10 沈惠申.功能梯度复合材料板壳结构的弯曲、屈曲和振动.力学进展,2004,34(1):53~60(Shen H S.Bending,buckling and vibration of functionally graded plates and shells .Advances In Mechanics,2004,34(1):53~60(in Chinese))
11 刘进,武兰河,张晓炜.功能梯度材料板的弯曲问题.石家庄铁道学院学报,2003,16(2):1~5(Liu J,Wu L H,Zhang X W.On bending of functionally graded rectangular plates.Journal of Shijiazhuang Railway Institute,2003,16(2):1~5(in Chinese))
12 王美芹,刘一华.具有梯度界面层的双材料悬臂梁解析解.应用力学学报,2010,27(2):232~238(Wang M Q,Liu Y H.Analytical solution for bi~material cantilever beam with graded interface layer.Chinese Journal of Applied Mechanics,2010,27(2):232 ~ 238(in Chinese))
13 陈镕,郑海涛,薛松涛等.无约束Timoshenko梁横向冲击响应分析.应用力学和数学,2004,25(11):1195~1201(Chen R,Zheng H T,Xue S T,et al.Analysis on transverse Impact response of an unrestrained Timoshenko beam.Applied Mathematics and Mechanics,2004,25(11):1195~1201(in Chinese))
14 陈镕,万春风,薛松涛等.Timoshenko梁运动方程的修正及其影响.同济大学学报(自然科学版),2005,33(6):711~715(Chen R,Zheng H T,Xue S T,et al.Modification of motion equation of Timoshenko beam and Its effect.Journal of Tongji University,2005,33(6):711 ~715(in Chinese))
15 陈镕,万春风,薛松涛等.无约束修正Timoshenko梁的冲击问题.力学学报,2006,38(2):262~268(Chen R,Zheng H T,Xue S T,et al.Impact response of an unrestrained modified Timoshenko beam.Chinese Journal of Theoretical and Applied Mechanics,2006,38(2):262 ~268(in Chinese))
16 吴晓,罗佑新.用Timoshenko梁修正理论研究功能梯度材料梁的动力响应.振动与冲击,2011,30(10):245~248(Wu X,Luo Y X.Dynamic responses of a beam with functionally graded materials with Timoshenko beam correction theory.Journal of Vibration and Shock,2011,30(10):245~248(in Chinese))
17 李清禄,李世荣.功能梯度材料梁在后屈曲构形附近的自由振动.振动与冲击,2011,30(9):76 ~78,135(Li Q L,Li S R.Free vibration of FGM Euler beam with post-buckling configuration subjected to axial force.Journal of Vibration and Shock,2011,30(9):76 ~78,135(in Chinese))
*The project supported by the construct program of the key discipline in Hunan province(Mechanical Design and Theory)and the Natural Science Foundation of Hunan Education Committee(11A081)
† Corresponding author E-mail:wx2005220@163.com
STUDY ON VIBRATION CHARACTERISTIC OF BI-MATERIAL CANTILEVER BEAM WITH GRADED INTERFACE LAYER
BY TIMOSHENKO BEAM CORRECTIVE THEORY*
Wu Xiao†Luo Youxin Huang Chong Yang Lijun
(Hunan University of Arts and Science,Changde415000,China)
The vibration characteristic of the bi-material cantilever beam with graded interface layer was studied by Timoshenko beam corrective theory.The neutral axis site of the bi- material cantilever beam with graded interface layer was determined by the static equilibrium equations and the vibration equations of bi- material cantilever beam with graded interface layer were also established by Timoshenko beam corrective theory,the expression for natural frequency of it and the analytical solution for forced vibration of it under the action of harmonic load were obtained.The effect of neutral axis site to vibration characteristic of bi-material cantilever beam with graded interface layer was discussed.Analysis of examples indicates that the height of graded interface layer had more greatly influence on vibration characteristic of bi- material cantilever beam with graded interface layer.
timoshenko beam, graded interface layer, neutral axis, vibration
26 June 2012,
27 December 2012.
10.6052/1672-6553-2013-043
2012-06-26 收到第 1 稿,2012-12-27 收到修改稿.
*湖南省“十二五”重点建设学科(机械设计及理论)、湖南省教育厅项目(11A081)
E-mail:wx2005220@163.com

