色噪声激励下三势阱系统逻辑随机共振研究*
张慧清 徐伟 许 勇
(西北工业大学应用数学系,西安 7 10072)
色噪声激励下三势阱系统逻辑随机共振研究*
张慧清†徐伟 许 勇
(西北工业大学应用数学系,西安 7 10072)
本文利用基于Simulink的数值模拟方法研究了高斯色噪声激励下三势阱系统的逻辑随机共振现象.首先对于独立的加性和乘性高斯色噪声激励下的三势阱系统,发现仅有加性噪声作用不能实现可靠的逻辑操作,但加性噪声和乘性噪声共同作用可诱导良好的逻辑随机共振现象.和高斯白噪声相比较,高斯色噪声激励下能产生可靠逻辑随机共振的(D,Q)平面上的区域范围更大.进一步讨论了加性和乘性噪声之间的关联对于逻辑随机共振现象的影响,发现噪声关联对逻辑随机共振现象起着破坏性的作用.
逻辑随机共振, 三势阱系统, 高斯色噪声
引言
随机共振是由Benzi等[1]首先提出的,它反映了噪声对于非线性系统所起的积极作用,一定量的噪声可增强系统的响应.目前,随机共振成为了非线性领域研究的热点,其理论方面近年的发展及在物理化学等领域的应用可见Gammaitoni等的综述性文章[2].近年来,非高斯噪声诱导随机共振现象得到了广泛的关注,例如Duffing系统中Levy噪声诱导的随机共振现象已被研究[3].
随着现代科技的发展,对数字电路精度的要求不断提高,噪声成为了电路设计中不可忽略的因素.能否利用噪声和非线性的协同作用成了电路设计的关键问题,为了将随机共振的思想和电路设计结合来更好的利用电路中的噪声,Murali等[4]提出了逻辑随机共振的概念.他们研究了一非常简单的非线性系统,当系统输入包含两个随机方波时,输入和输出是某种逻辑关联的关系,通过调整系统参数可执行不同的逻辑操作.随后,逻辑随机共振现象得到了广泛的研究.例如,Zhang[5]研究了加性高斯色噪声对于双稳系统随机共振的影响,发现了成功率曲线随关联时间增加而右移以及关联时间在某个区域内成功率才接近1的现象.Bulsara等[6]研究了乘性高斯白噪声对于逻辑随机共振现象的影响.Singh等[7]发现了光学双稳系统中的逻辑随机共振现象.Dari等[8]考察了关联高斯白噪声对于基因网络系统的影响.Wu等[9]研究了系统耦合对于逻辑随机共振的影响,发现和单个双稳系统比较,耦合系统可产生可靠逻辑操作的噪声范围更宽.针对双稳系统有可能出现信息丢失的现象,Storni等[10]研究了加性高斯白噪声激励下势函数为分段光滑的三势阱系统的逻辑随机共振现象,可实现多种逻辑操作.
本文首先研究独立加性和乘性高斯色噪声激励下三势阱系统的逻辑随机共振现象,进一步研究加性和乘性色噪声之间的关联对于逻辑随机共振的影响.
1 系统模型
考虑一粒子沿三势阱系统的运动,其相应的郎之万方程为[11]

其中U(x)=x2(bx2-c)2为对称的势函数,中间阱代表了反应态,两边阱代表了平行反应的生成态.b,c是系统参数,γ为耗散常数.本文中令 b =0.1,c=1,γ=1.ξ(t)和η(t)是均值为零的 O rnstein-Uhlenbeck过程,由如下微分方程生成

其中ξw(t),ηw(t)为均值为零的高斯白噪声,满足:

Q和D为噪声强度,λ为噪声关联强度,当λ=0时,噪声独立.当噪声关联时间τi→0(i=1,2)时,高斯色噪声退化为高斯白噪声.I(t)=I1(t)+I2(t)为逻辑输入信号.(I1,I2)构成了四个不同的逻辑输入集(0,0),(0,1),(1,0),(1,1).令 Ii(i=1,2)取-0.8相应于逻辑输入0,取0.8相应于逻辑输入1.通过改变逻辑输出的值来实现不同的逻辑操作(表1).

表1 不同逻辑门输出的定义Table 1 Definitions of the outputs for different logic gates
经典随机共振理论中常用信噪比作为随机共振的度量.类似的,为了量化逻辑随机共振,Murali等[4]引入了成功率的概念:

每次运行包括了四个不同逻辑输入集(0,0),(0,1),(1,0),(1,1)的所有可能的排列.当成功率近似为1时,认为发生了可靠的逻辑操作.

图1 Simulink仿真图Fig.1 Simulink simulation diagram
本文采用基于Simulink的数值模拟方法来研究高斯色噪声对于成功率的影响,仿真图见图1.
2 数值仿真结果
图2显示了噪声独立且 D=0.01,τ2=0.1 时成功率作为乘性噪声强度的变化曲线.可看出当噪声关联时间固定时,存在特定的噪声窗口使得成功率接近1,即乘性噪声可诱导逻辑随机共振.由图2还可看出随噪声关联时间的增加,优化噪声窗口右移且宽度变宽.和高斯白噪声情形比较,高斯色噪声需要的噪声更强范围更广,这使得较大噪声情形下也有可能产生可靠逻辑随机共振.

图2 成功率P作为乘性噪声强度Q的函数其中 λ =0,D=0.01,τ2=0.1.Fig.2 The success probability P versus multiplicative noise strength Q with λ =0,D=0.01,τ2=0.1.
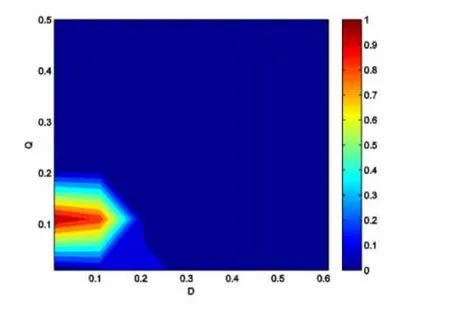
图3 成功率随加性和乘性噪声强度的变化λ =0,τ1= τ2=0.Fig.3 The success probability P as a function of versus multiplicative noise strength Q and additive noise strength D with λ =0,τ1= τ2=0.
图3显示了加性和乘性噪声独立且都是高斯白噪声时(D,Q)平面上产生可靠逻辑随机共振的区域.图4显示了高斯色噪声情形下τ1=τ2=1时(D,Q)平面上产生可靠逻辑随机共振的区域.两图比较可看出高斯色噪声下产生可靠逻辑操作的噪声窗口范围比高斯白噪声情形下更广.

图4 成功率随加性和乘性噪声强度的变化λ =0,τ1= τ2=1.Fig.4 The success probability P as a function of versus multiplicative noise strength Q and additive noise strength D with λ =0,τ1= τ2=1.
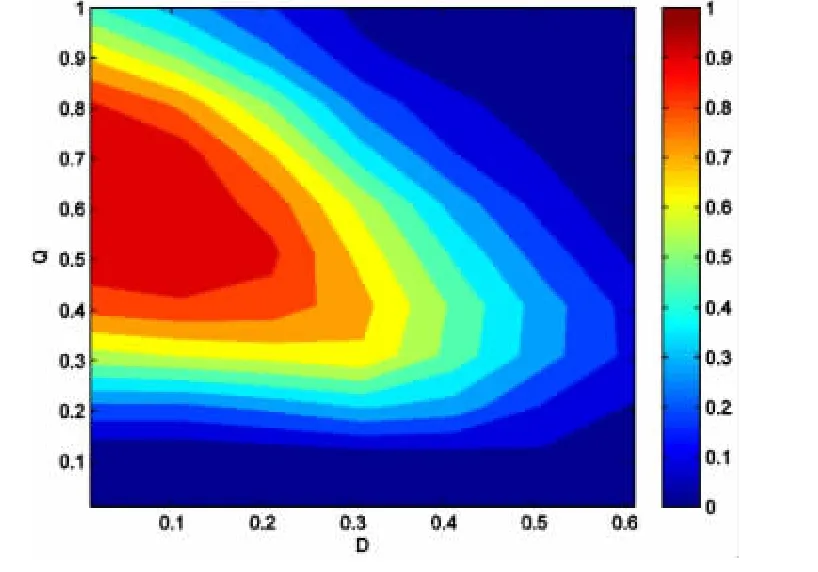
图5 成功率随加性和乘性噪声强度的变化λ =0,τ1= τ2=3.Fig.5 The success probability P as a function of versus multiplicative noise strength Q and additive noise strength D with λ =0,τ1= τ2=3.

图6 成功率随加性和乘性噪声强度的变化λ =0.9,τ1= τ2=3.Fig.6 The success probability P as a function of versus multiplicative noise strength Q and additive noise strength D with λ =0.9,τ1= τ2=3.
图5显示了噪声独立时,随噪声关联时间的增加,优化噪声窗口范围进一步扩大.图6是噪声关联情形下成功率随加性、乘性噪声强度的变化情况,和图5对比可看出随噪声关联强度的增加,优化噪声窗口急剧收缩,由此显示了噪声的关联对于逻辑随机共振现象起着破坏性的作用.另外,从图4~6还可看出加性噪声不能单独诱导逻辑随机共振现象,乘性噪声出现才可产生可靠的逻辑操作.
3 结论
本文利用数值模拟方法研究了高斯色噪声激励下三势阱系统的逻辑随机共振现象.研究结果表明仅仅出现加性噪声不能产生好的逻辑随机共振现象,乘性噪声的出现才能诱导逻辑随机共振.另外,和高斯白噪声比较,高斯色噪声产生逻辑随机共振的范围更广.本文进一步研究了关联噪声对于逻辑随机共振的影响,发现加性和乘性噪声之间的关联对于逻辑随机共振现象起着破坏性的作用.
1 Benzi R,Sutera A.The mechanism of stochastic resonance.Journal of Physics A:Mathematical and General,1981,14:453~457
2 Gammaitoni L,Hanggi P,Jung P and Marchesoni F.Stochastic resonance.Reviews of Modern Physics,1998,70:223~288
3 李娟娟,许勇,冯晶.Duffing系统中Levy噪声诱导的随机共振与相转移.动力学与控制学报,2012,10(3):278~282(Li J J,Xu Y,Feng J.Lévy noise induced the stochastic resonance and phase transition in Duffing system.Journal of Dynamics and Control,2012,10(3):278 ~ 2 82(in Chinese))
4 Murali K,Sinha S,Ditto W L and Bulsara A R.Reliable logic circuit elements that exploit nonlinearity in the presence of a noise floor.Physical Review Letters,2009,102:104101
5 Zhang L,Song A G and He J.Effect of colored noise on logical stochastic resonance in bistable dynamics.Physical Review E,2010,82:051106
6 Bulsara A R,Dari A,Ditto W.L,Murali K,Sinha S.Logical stochastic resonance.Chemical Physics,2010,375:424~434
7 Singh K P and Sinha S.Enhancement of“logical”response by noise in a bistable optical system.Physical Review E,2011,83:046219
8 Dari A,Kia B,Bulsara A.R,Ditto W.L.Logical stochastic resonance with correlated internal and external noises in a synthetic biological logic block.Chaos,2011,21:047521
9 Wu H,Jiang H J,Hou Z H.Array-enhanced logical stochastic resonance in coupled bistable systems.ChineseJournal of Chemical Physics,2012,25:70~76
10 Storni R,Ando H,Aihara K,Murali K and Sinha S.Manipulating potential wells in logical stochastic resonance to obtain XOR logic.Physics Letters A,2012,376(8):930~937
11 Ghosh P K,Bag B C,Ray D S.Noise correlation-induced splitting of Kramers'escape rate from a metastable state.The Journal of Chemical Physics,2007,127:044510
*The project supported by the National Natural Science Foundation of China(10972181,11102157,1117223)and NPU Foundation for Fundamental Research
† Corresponding author E-mail:huiqingzhang@nwpu.edu.cn
THE STUDY OF LOGICAL STOCHASTIC RESONANCE IN A TRIPLE-WELL POTENTIAL SYSTEM WITH COLORED NOISE*
Zhang Huiqing†Xu WeiXu Yong
(Department of Applied Mathematics,Northwestern Polytechnical University,Xi'an710072,China)
In this paper,the logic stochastic resonance(LSR)phenomenon in a triple-well potential system is investigated by performing Simulink simulation.When the additive noise and multiplicative noise are uncorrelated,it is shown that LSR can be successfully induced by multiplicative Gaussian colored noise instead of additive noise.Compared with the Gaussian white noise,the reliable region in plane(D,Q)expands with increasing noise color.Furthermore,we find that the LSR is destroyed by the correlation between the additive noise and multiplicative noise.
Logical stochastic resonance, triple-well potential system, Gaussian colored noise
11 June 2012,
13 June 2012.
10.6052/1672-6553-2013-050
2012-06-11 收到第 1 稿,2012-06-13 收到修改稿.
*国家自然科学基金资助项目(10972181,11102157,11172233)、西北工业大学基础研究基金资助项目
E-mail:huiqingzhang@nwpu.edu.cn

