三角形一个优美结论的空间拓广
2013-09-17 01:13:34福建省大田市第一中学田富德邮编366100
中学数学教学 2013年2期
福建省大田市第一中学 田富德 (邮编:366100)
2011日本数学奥林匹克有如下一道题:
设H是锐角ΔABC的垂心,M是边BC的中点,过点H作AM的垂线,垂足为P.证明:AM·PM=BM2.
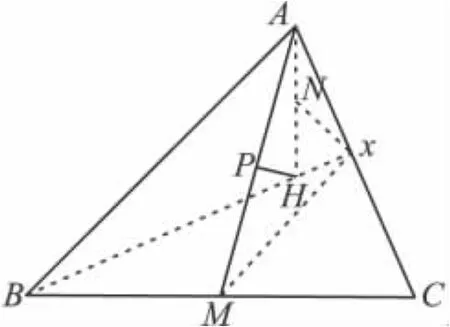
图1
证法1 如图1,设BH与AC交于点X,AH的中点为N.
因为 ∠AXH= ∠APH=90°,所以,点P、X在以AH为直径的圆上(若AB=AC,则P、H重合,X也在以AH为直径的圆上).于是,∠AXN=∠XAN.
又因为∠BXC=90°,所以,点X在以BC为直径的圆上.
易知,∠CXM= ∠XCM,且XM=BM.
由∠NXM=180°-(∠AXN+∠CXM)=180°-(∠XAN+∠XCM)=90°,
则MX与以AH为直径的圆切于点X.
于是,AM·PM=MX2=BM2.


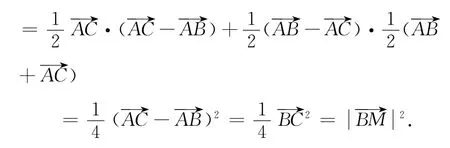
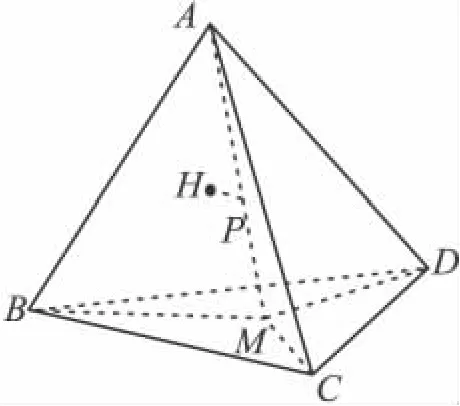
图2
文[1]提供了以上证法1,纯几何证法巧妙,作辅助线是关键.由于试题需要证明的是线段的数量关系,故笔者借助于向量给出了证法2.向量方法避免了作辅助线的困难,也易于推广,从证法2的证明过程中,知试题条件中的“锐角三角形”可以改为“任意三角形”.
众所周知,四面体四条高并不一定交于一点,也就是说不一定有通常意义下的垂心.经过笔者探究,倘若四面体四条高交于一点,则保留了试题的优美性质,向量方法在几何证明中的体现了强大功能.现以定理形式,叙述如下:
定理 设四面体ABCD四条高交于一点H,M是面BCD的重心,过点H作AM的垂线,且垂线与直线AM相交于点P,则有




故有18AM·PM=BC2+CD2+DB2.
1 中等数学编辑部.2010-2011国内外数学竞赛题及精解[J].中等数学,2012增刊(2)
猜你喜欢
中学数学研究(2024年3期)2024-04-05 16:02:32
科普童话·学霸日记(2023年7期)2023-08-21 09:49:46
新世纪智能(教师)(2021年2期)2021-11-05 08:43:18
小学生学习指导(中年级)(2021年10期)2021-11-01 08:17:08
数学物理学报(2021年4期)2021-08-30 08:27:52
海洋通报(2021年2期)2021-07-22 07:55:26
数学物理学报(2021年2期)2021-06-09 08:54:24
天府数学(2020年3期)2020-09-10 19:53:46
河北理科教学研究(2020年1期)2020-07-24 08:14:34
数学学习与研究(2016年1期)2016-07-04 13:18:37

