“立体几何”专题复习的五个切入点

安徽省太湖中学 李昭平 （邮编：246400）

纵观近几年的高考题，无论是全国卷还是省市自主命题卷，立体几何主要考查空间想象能力、思维能力和推理运算能力，考查重点仍然是空间的平行关系、垂直关系、三视图、空间角、距离的计算以及简单几何体的体积与表面积，题型涵盖选择、填空和解答题，一般稳定在一选一填一解答，分值大约占总分的14%左右.选择题、填空题以基础题和中档题为主.随着空间向量的引入，开辟了解证立体几何问题的新途径，进而大大降低了立体几何解答题的证明、作图与运算的难度.专题复习应关注以下五个切入点，能有效掌握立体几何的核心知识与方法，并与相关知识融会贯通，提高解决立体几何问题的能力.

切入点1 以三视图与简单组合体为载体的问题

三视图与简单组合体是新课标实验教材的新增内容，对空间想象能力要求较高，从这一点看，新教材与老教材对学习立体几何的主要目标是不变的.不过新教材的编排顺序与老教材正好相反，它是先安排柱体、锥体、台体、球体等内容，然后再学习空间中的线面位置关系.

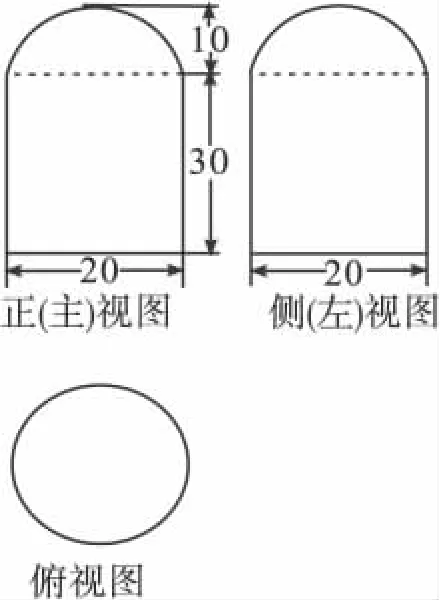
例1 如右图是不锈钢保温饭盒的三视图，根据图中数据（单位：cm），求得该饭盒的表面积为（ ）

A.1100πcm2

B.900πcm2

C.800πcm2

D.600πcm2

思路 由三视图想象出简单组合体的直观图，再用相关公式求饭盒的表面积.

解析 由三视图可知，该饭盒是一个圆柱和半球的组合体，圆柱的底面半径为10cm米，高为30cm米，半球的半径为10cm，则S圆柱＝2πrh＋πr2＝700π.

S半球＝2πr2＝200π，所以这个饭盒的表面积为900πcm2，故选B.

例2 如右图，某个柱体的正（主）视图、侧（左）视图都是面积为1的正方形，且其体积为，那么这个柱体的表面积可以（ ）

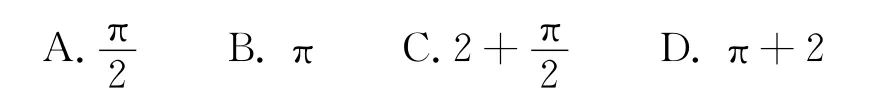
思路 判断猜想俯视图的形状，验证几何体的体积.

点评 从例1的解法中我们可以深刻地感受到：一旦将一个复杂的、抽象的问题落实到具体的、熟悉的图形中，将会变得非常简单.由三视图想象出简单组合体的直观图，是学习三视图的基本要求.对于根据三视图计算几何体的表面积问题，审题要严密.本题在解答时易出现的错误是把饭盒的表面积误认为是圆柱的表面积与半球的表面积之和，从而导致错误答案.例2打破由三视图计算几何体表面积或体积的传统题型，而已知体积反过来确定几何体的形状和表面积，这种逆向设置问题具有发散性和开放性，能有效考查学生的想象力和思维力，要引起重视.

切入点2 以球体与特殊多面体的切接为载体的问题

特殊多面体中既包含了空间中许多平行关系、垂直关系，又与球体有紧密的联系，因此往往受到高考命题者的青睐.近几年的高考中常常出现球体与特殊多面体的切接问题.解答此类问题的关键是找到球心，以及球的直径、半径与多面体棱长之间的关系.

例 3 如图，△ABC中，∠ABC＝ 90°，PA⊥平面ABC，且PC＝a.求三棱锥P—ABC外接球的表面积.

思路 寻找三棱锥P—ABC外接球的球心.

解析 因为PA⊥平面ABC，所以PA⊥BC，PA⊥AC.

而∠ABC＝90°，AB⊥BC，所以BC⊥平面PAB，所以BC⊥PB.

取PC的中点O，则OA＝PC＝OB＝OP＝OC.故外接球的球心是O，半径是OA＝PC＝.于是三棱锥P—ABC外接球的表面积S＝4π·OA2＝πa2.

例4 甲烷分子（CH4）由一个碳原子和四个氢原子组成，其空间图形为一个各条棱都相等的四面体，其中四个氢原子分别位于该四面体的四个顶点上，碳原子位于该四面体的中心，它与每个氢原子的距离都相等.若视氢原子、碳原子为一个点，四面体的棱长为a，则碳原子到各个氢原子的距离是____________.

思路 利用球体与正四面体、正方体的关系求解.

解析 四面体的四个顶点在以中心（碳原子）为球心，中心到各顶点（氢原子）的距离为半径的球面上.

如图，将此四面体ABCD补成正方体BD′，其中A′、B′、D′也在球面上.设碳原子到每个氢原子的距离为x，则2x＝BD′，BD′、AB、AA′之间的关系是a＝AB＝AA′，2x＝BD′＝AA′，因此，2x＝·，得x＝a.

点评 例3由于是非特殊的多面体，所以关键要寻找球心，有一定的难度.注意正方体、正四面体、长方体、三条侧棱两两垂直的三棱锥、正八面体的外接球的半径与这些特殊多面体的棱的联系，大家可以探讨一下.这类问题在高考中多以选择题、填空题的形式出现，具有一定的创新性，补形法、构造法常常帮助我们速战速决.

切入点3 以线线、线面、面面关系为载体的问题

空间中线线、线面、面面关系是立体几何的核心内容，其中又以线面的平行与面面的垂直问题为重点.熟练掌握线面平行、面面垂直的判定和性质是迅速解决问题的关键.

例5 如图，多面体ABCDEF中，四边形ABCD是边长为2a的正方形，平面ADEF垂直于平面ABCD，且FA⊥AD，EF∥AD，EF＝AF＝a.

（1）若P、Q分别为棱BF和DE的中点，

求证：PQ∥平面ABCD；

（2）求多面体ABCDEF的体积；

（3）求二面角A－BD－E的余弦值.

思路 寻求关系，体积转化，建系用向量法求解.

解析 （1）取AB的中点S，连结PS.作EM⊥AD于M，取MD的中点T，连结QT.

于 是PS∥AF，PS＝AF，QT∥EM，QT＝EM.因为FA⊥AD，EF∥AD，EF＝AF＝a，所以AMEF是正方形，所以AFEM.故PSQT，四边形PSTQ是平行四边形，所以PQ∥ST.

而ST⊂平面ABCD，PQ⊄平面ABCD，所以PQ∥平面ABCD.

（2）因为平面ADEF垂直于平面ABCD，且FA⊥AD，所以FA⊥平面ABCD.

又CD⊥AD，所以CD⊥平面DEF.

（3）以点A为原点，射线AB，AD，AF分别为x，y，z轴，建立空间直角坐标系O－xyz.

设a＝1，则F（0，0，1），B（2，0，0），D（0，2，0），E（0，1，1），＝ （－2，1，1），＝ （－2，2，0）.

设n＝ （x，y，z）是面EBD的法向量，则n·＝n·＝0，即

例6 如图，正三棱柱ABC—A1B1C1的底面边长为2，点E、F分别是棱CC1、BB1上的点，点M是线段AC上的动点，EC＝2FB＝2.

（1）当点M在何位置时，MB／／平面AEF？

（2）当MB／／平面AEF时，求直线MB到平面AEF的距离.

思路 根据正三棱柱中的垂直关系建立空间直角坐标系（要注意 ∠ACB＝60°，慎求B、F的坐标），再将向量关系代数化，通过向量的坐标运算和点面距离公式就能很快确定点M的位置和直线MB到平面AEF的距离.

解析 （1）如图，建立空间直角坐标系B—xyz，则C（0，0，0），E（0，0，2），A（2，0，0），F（1，，1），B（1，0）.

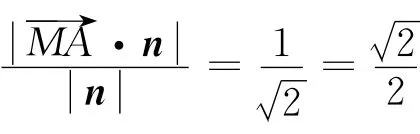
切入点4 以平面向空间类比为载体的问题

将“平面图形的性质类比到空间，探求相应的空间图形是否也有此类似的性质”，称之为“类比推广”型立几开放题.这种开放题往往以平面图形的性质及其证法为基础，融探索、猜想、证明于一体，能有效考查学生的空间想象能力、类比联想能力、合情推理能力以及创新能力，在近几年的高考中是高频考点，要引起关注.

思路 将三角形的边类比到空间四面体的面，面积之比类比到空间上的体积之比，“面积法”类比到“体积法”.

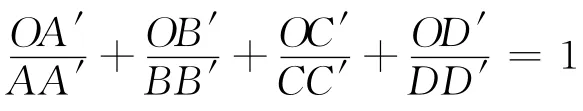
事实上，如图，设O为四面体ABCD内任意一点，连结AO、BO、CO、DO并延长，分别交 对 面 于A′、B′、C′、D′四点，则

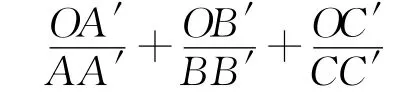
例8 我们知道：在平面几何中，△ABC的三条中线相交于一点，这个点叫三角形的重心.重心分中线之比为2∶1（从顶点到中点）.据此，我们拓展到空间：把空间四面体的顶点与对面三角形的重心的连线叫空间四面体的中轴线，则四条中轴线相交于一点，这点叫此四面体的重心.类比上述命题，写出四面体重心的性质，并证明.

思路 将三角形重心性质的证明方法类比到空间四面体中，利用相似三角形对应边成比例.

解析 事实上，如下图，AE、BP为四面体的中轴线，P、E分别为ΔACD、ΔBCD的重心.

连结PE.因为AP∶PF＝2∶1，BE∶EF＝2∶1，所以AP∶PF＝BE∶EF，PE∥AB.

因此AG∶GE＝BG∶GP＝PE∶AB＝3∶1.

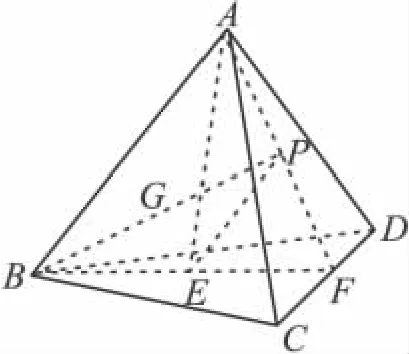
所以，空间四面体的重心分顶点与对面三角形的重心的连线之比为3∶1（从顶点到对面三角形的重心）.

点评 一般地，平面上的“点、线、面”类比到空间上的“线、面、体”（元素类比）；平面上的数量结构形式类比到空间上的数量结构形式（结构类比）；平面上“面积法”类比到空间上的“体积法”，平面上“相似法”类比到空间上的“相似法”（方法类比）.

切入点5 以平面图形折成立体图形为载体的问题

“平面折叠型”问题是近几年高考考查立体几何的热点，即将平面图形通过折叠变成立体图形，让静止问题动态化，使得对立体几何的考查显得更加丰富多彩.解决此类问题的关键是，要对折叠前后两个图形进行观察，弄清折叠前后，哪些位置关系与度量关系没有变化，哪些位置关系与度量关系有变化.复习中要注重从多角度、多层次、多侧面思考与探究，沟通相关知识与方法之间的内在联系，训练发散思维，更好把握这类问题.

例9 正三角形ABC的边长为a，将它沿平行于BC的线段PQ折起（其中P在AB边上，Q在AC边上），使平面APQ⊥平面BPQC.若折叠后，A、B两点间的距离为d，求d的最小值.

思路 画出折叠前后的平面图形和空间图形，观察折叠前后位置关系与度量关系的变化情况.

解析 作AD⊥PQ于D，则D为PQ的中点.因为平面APQ⊥平面BPQC，所以AD⊥平面PBCQ.连结BD，则d2＝AD2＋BD2.

设AD＝x，DE＝a－x（E为BC的中点），于是BD2＝DE2＋BE2＝，

例10 平行四边形ABCD中，AB⊥BD，4AB2＋2BD2＝1，沿BD将四边形折成直二面角，求三棱锥A—BCD外接球的体积.

思路 观察折叠前后位置关系与度量关系的变化情况，寻找三棱锥A—BCD外接球的球心.

解析 如图，因为平面BDC⊥平面ABD（折成直二面角），

而AB⊥平面BDC，CD⊥平面ABD，所以

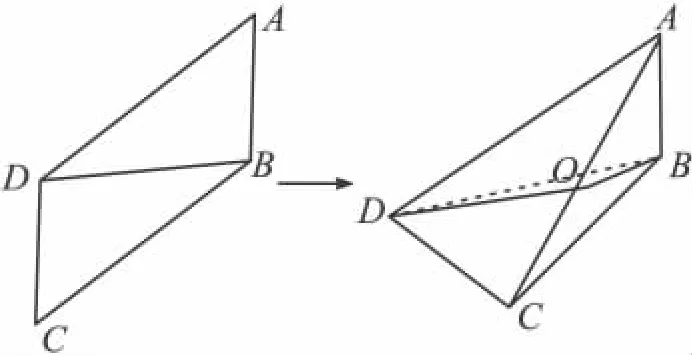
AB⊥BC，CD⊥AD.取AC的中点O，则OA＝OB＝OC＝OD.于是外接球的球心是O，OA＝AC，OA2＝AC2.

而AC2＝AB2＋BC2＝2AB2＋BD2＝（4AB2＋2BD2）＝.

半径是OA＝AC＝.于是外接球的体积V＝·OA2＝.

点评 例9将正三角形折成了一个直二面角，折叠后的ΔAPQ、梯形BPQC与折叠前的不变，只是位置发生了改变（垂直）.A、B两点间的距离发生了变化，且随平行线PQ位置的变化而变化.因此要建立d关于x的目标函数，利用函数求d的最小值.例10的平行四边形一条对角线与一边垂直，先注意正确画图，再利用折叠前后垂直不变性和度量不变性求解.

以上介绍的五个切入点，很好地体现了立几中的核心知识和重要思想方法（转化、化归、类比、构造、折叠、建系等）.需要注意的是，由于新课标教材体系、结构、内容的变化和高考能力立意思想的加强，立体几何问题的题型、内容、背景、设置方式以及解题方法都有较大的变化，与相关知识交汇的力度也在不断加大，而且选择题或填空题的位置逐渐后移，并常常作为选择题或填空题的压轴题、以创新题的面貌出现在试卷之中.因此，我们在切实掌握基础知识、基本技能和基本方法的基础上，还要重视动手操作能力的训练和对新题型的探究，在高考中以不变应万变.