程序框图与随机模拟的“友情客串”
安徽省合肥第一中学 杜明成 (邮编:230601)
纵观近年各省的高考题,如稍加留神,便可以发现,程序框图这颗奇葩常开不谢.而且各省更加注重程序框图与其它知识相交汇融合,使得程序框图的内容焕发出新的活力.程序框图给我们感觉是“一图抵百语”,其思想是非常重要的,但并不神秘.为把握程序框图与随机模拟交汇的脉搏,现以2012年陕西高考卷中涉及的程序框图题为例,并通过一题两变,挖掘程序框图与随机模拟交汇性考题的特点及其求解策略,以达到知己知彼、有的放矢.
例1 (2012年陕西省高考题)下图是用模拟方法估计圆周率π的程序框图,P表示估计结果,则图中空白框内应填入( ).
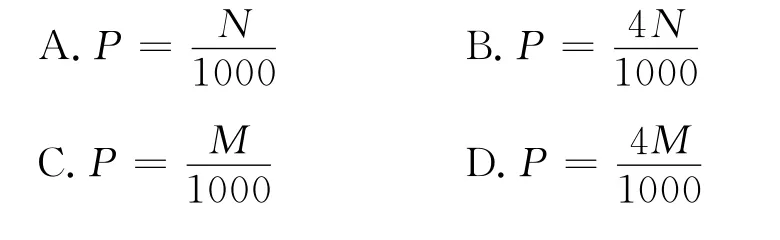
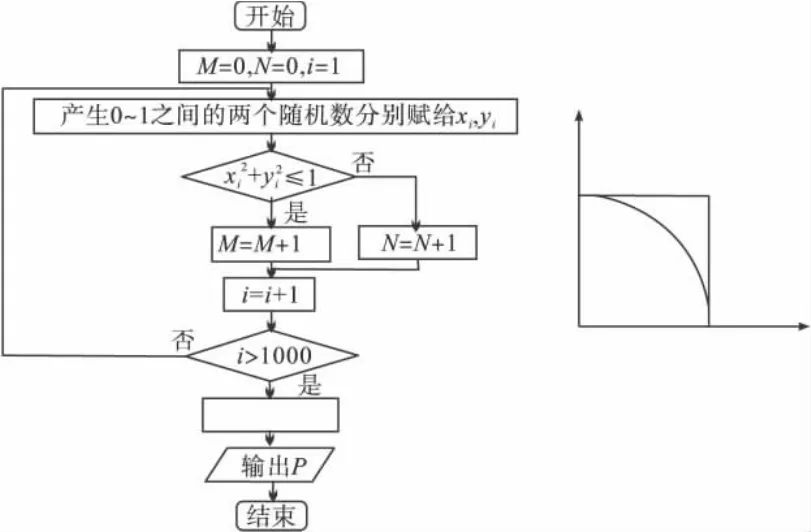
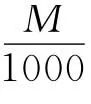
评析 本题的“闪光”之处是将随机模拟、几何概型融入程序框图中,给人耳目一新之感.意在考查程序框图的读图能力、文字语言、图象语言、符号语言间的转译能力及推理运算求解能力.求解此类跨度较大的交汇题的关键要过好两关:一是读图有方:读懂程序框图的意义,并将其运用到新的情境中.如本题,读懂程序框图中的循环结构的含义,识别其循环所需要的条件与循环体;二是运算有招:会利用几何概型的测度与概率公式(当考察对象为点,点的活动范围在平面区域内时,用面积比计算),探求其概率,从而通过列方程来识别处理框应填写的内容.
仍用例1中的随机模拟的背景,以程序框图为载体,把“估计圆周率π”变更为“估计抛物线y=x2与直线x=1、x轴所围成的图形的面积”,并把原来的选择题变为填空题,得如下的变式题:
变式1 在用模拟试验估算如图1阴影部分(抛物线y=x2与直线x=1、x轴所围成的图形)面积时,利用计算机产生[0,1]上的两个随机数得到一个点(x,y),现试验100次,得到100个点:(x1,y1),(x2,y2),(x3,y3),…,(x100,y100).为了统计落入图1阴影部分的点的个数,设计如图2所示的程序框图:
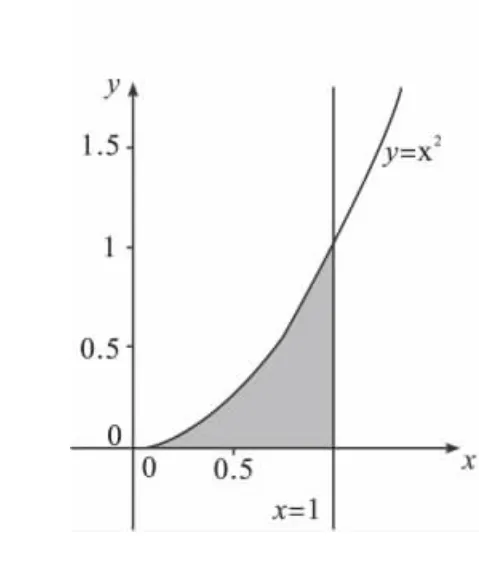
图1
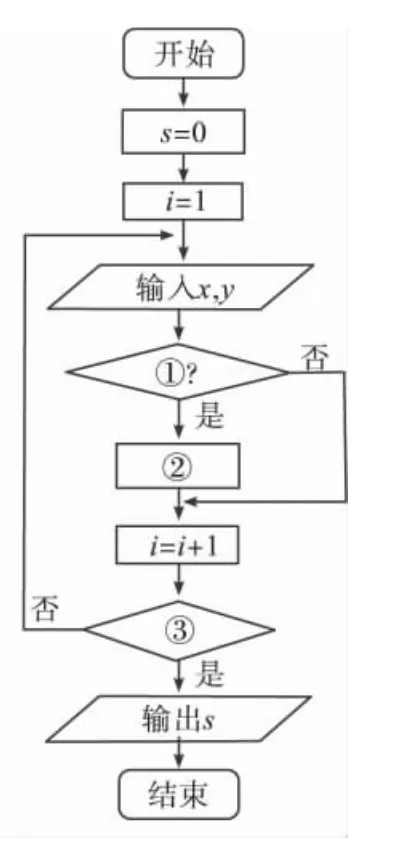
图2
请把图2中的程序框图补充完整,其中①__________,②__________,③__________.
解析 按照程序框图的箭头流向读,可知s=0,i=1,输入随机数x,y,观察图1的阴影部分,可知图2中的①处应填写“y<x2”,如果y<x2,那么此点就落在图中的阴影部分,因此执行s=s+1,即②处应填写“s=s+1”.因为要统计100个点,程序框图是直到型循环结构,故判断框内应填写的条件是“i>100”.即应填:①y<x2;②s=s+1;③i>100.
评析 本变式题貌似平凡,但意境幽深,把研究圆周率的估值问题提升到对不规则图形的面积的估值问题.旨在考查考生接受和处理新信息的能力,它能有效地考查考生独立获取信息、加工信息及后继学习的能力.难度比例1略有拔高,如能准确读懂程序框图之间隐含的信息,并辅之以函数图象去判断,即可准确地推断出两个判断框与一个处理框内应填写的内容.
把变式1中的“把程序框图补充完整”,变更为“估算阴影部分的面积”,可得如下的变式题:
变式2 条件同变式1,若执行该程序框图(图2)后得到s=30,试根据该结果估算图1中的阴影部分面积为( )
A.0.2 B.0.3 C.0.4 D.0.5
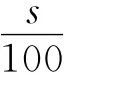

评析 变式2与变式1不一样的是在已知条件中没有告诉程序框图的功能,而是让学生通过图1与图2去读懂程序框图的功能:统计落入图1阴影部分的点的个数.从而估计阴影部分的面积也就“水到渠成”.
由以上一题两变可提炼出求解程序框图与随机模拟相交汇试题的“双步曲”:第一步,“会赏图”即能读懂已知程序框图所隐含的信息,并会进行信息提取,对于常见的顺序结构、循环结构与条件结构要熟悉,能做到看图悟其意;第二步,“会运算”即对程序框图所反馈的信息进行提取,并结合几何概型的概率公式等进行运算.有关随机模拟与程序框图相交汇的命题视角,值得我们关注与期待.

