一个猜想不等式及其部分解决

上海市宝山区宝林路宝林六村42号101室 姜坤崇 （邮编：201999）

本文给出关于三元a、b、c的一个猜想不等式及其部分解决.

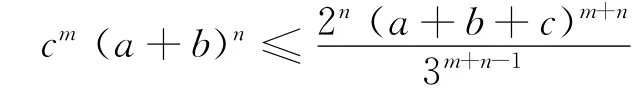
1 当m＝n＝1时猜想不等式的证明

结论1 设a、b、c是正实数，则

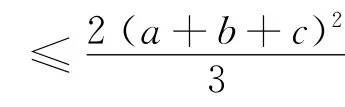
证明 由二元均值不等式得

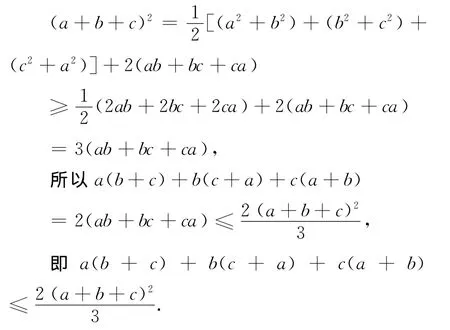
2 当m＝k，n＝2k（k是正整数）时猜想不等式的证明

结论2 设a、b、c是正实数，k是正整数，则

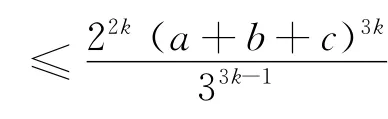
证明 由三元均值不等式得

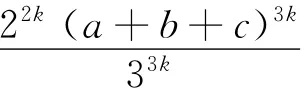
由结论2可得下面的一些不等式（其中a、b、c是正实数）：

3 当m＝k＋1，n＝2k（k是正整数）时猜想不等式的证明

结论3 设a、b、c是正实数，k是正整数，则

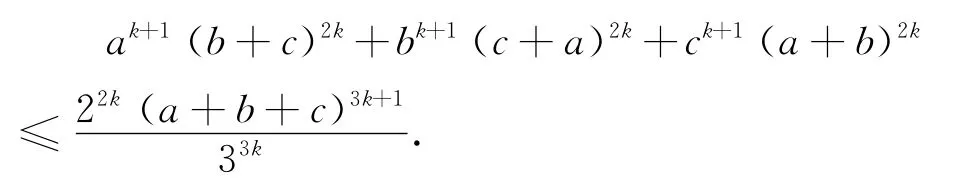
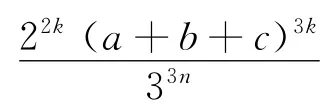
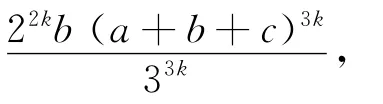
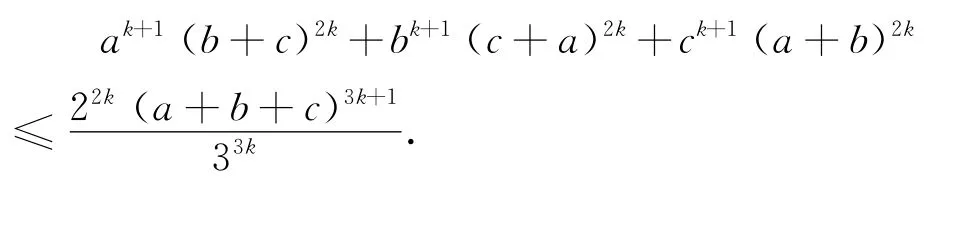
由结论3可得下面的一些不等式（其中a、b、c是正实数）：

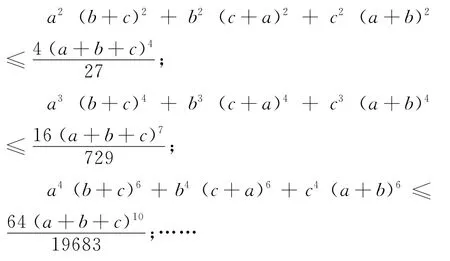
4 当m＝k，n＝2k＋1（k是正整数）时猜想不等式的证明

结论4 设a、b、c是正实数，k是正整数，则

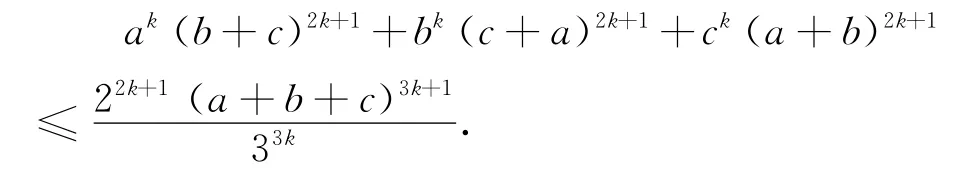
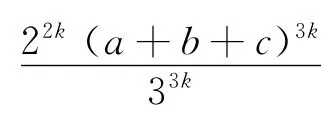
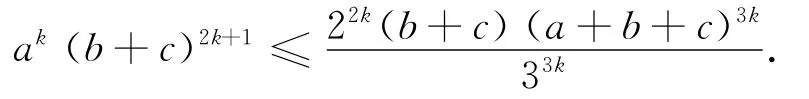
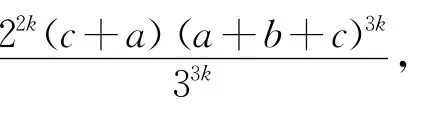
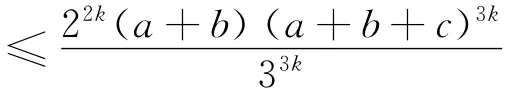
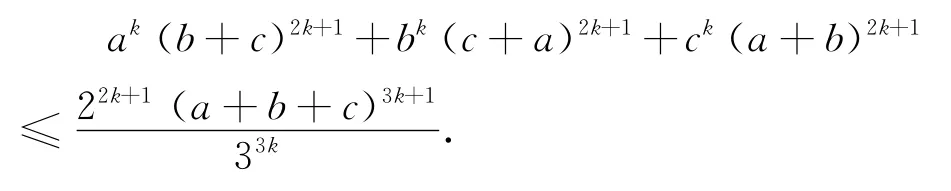
由结论4可得下面的一些不等式（其中a、b、c是正实数）：

5 当m＝1，n＝4；m＝2，n＝3时猜想不等式的证明

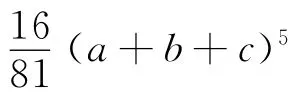
证明 由于所证不等式是关于a、b、c的5次齐次不等式，故可设a＋b＋c＝1，即证

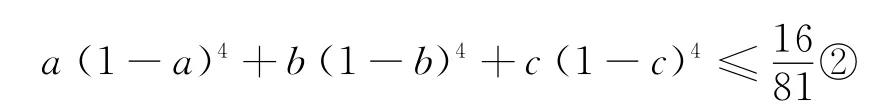
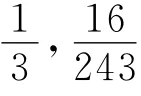
当x∈ （0，1）时，因为

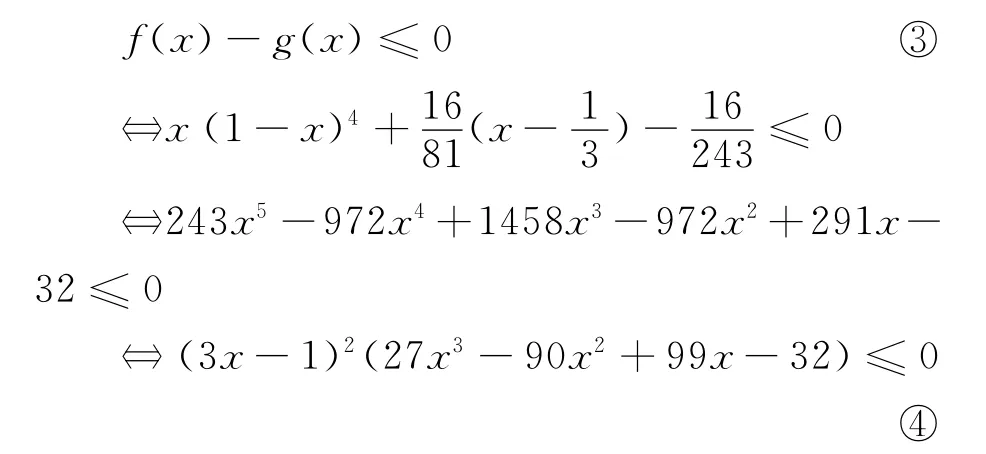
设h（x）＝27x3－90x2－99x－32，则h′（x）＝9（9x2－20x－11），由h′（x）在（0，1）上是减函数且h′（0）＝－99＜0知h′（x）＜0（其中x∈（0，1）），故h（x）在（0，1）上为减函数.

又h（0）＝－32＜0，所以h（x）＜0（其中x∈ （0，1）），所以 ④ 式成立，从而 ③ 式成立，于是

即②式成立，从而原不等式得证.

结论6设a、b、c＞0，则a2（b＋c）3＋b2（c＋a）3＋c2（a＋b）3≤（a＋b＋c）5.

证明 由于所证不等式是关于a、b、c的5次齐次不等式，故可设a＋b＋c＝1，即证

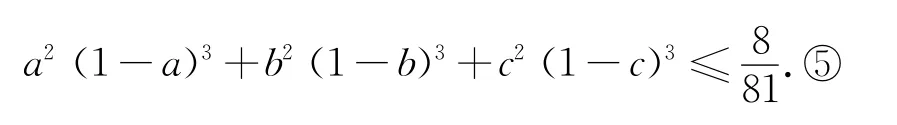
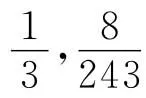
当x∈ （0，1）时，因为

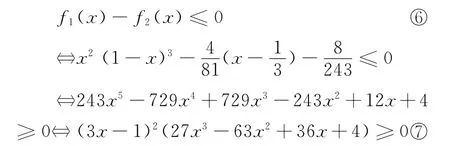
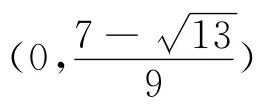
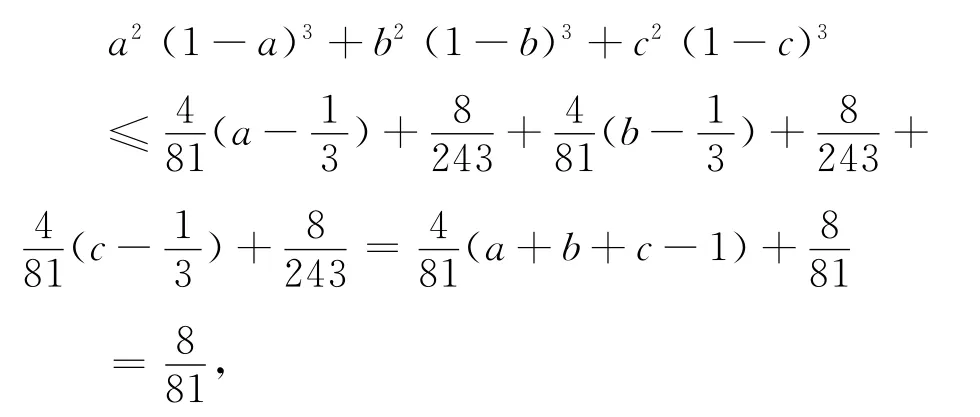
即⑤式成立，从而原不等式得证.

对于所有的正整数m、n（m≤n），猜想不等式是否完全成立？若成立，有无统一的证明？这些问题有待进一步探究解决.