数学学习中存在的“懂而不会、会而不能”现象的成因与对策——改良高考复习、提升高考成绩
江苏省宝应县曹甸高级中学 李兆江 (邮编:225803)
“懂而不会、会而不能”到“懂而会、会而能”体现了学生日趋完善的认知过程,这个过程受内因(自已学)与外因(教师教)共同推进.问题是数学的心脏,对学生数学学习中存在“懂而不会、会而不能”现象的成因与对策研究,自然离不开解决问题,更离不开高考.当下,全国的高三师生都在紧张有序备战2013年高考.此刻,若能充分关注学生数学学习中的“懂而不会、会而不能”现象并尽可能消除之,对改良高考复习、提升高考成绩无疑是大有裨益.下面,笔者就高三数学复习中存在“懂而不会、会而不能”现象的成因与应对策略和大家交流.
1 遵循教学规律、明确教学目的,消除“懂而不会、会而不能”现象
规律是指做事时必须要遵守的客观性、因果性、逻辑性、顺序性、层次性等内在规则.什么是教学规律?这里不再罗列.为了合理遵循教学规律,消除“懂而不会、会而不能”现象,笔者就当前教学实践中的一些现象作分析.
纵观当前的教学现状,教师是教得“多、乱、浅、累”,不能做到教得“精、清、透、轻(松).试卷如山,题目太多,苦练.讲条理,讲逻辑少.忽视理解,重视结果.忽视过程,忽视反思,忽视归纳总结.站得不高,看得不远,很少关注那些带观念性的、可以迁移的东西,学生则难以养成好的习惯,考场上难以举一反三、触类旁通.
做数学,不练习不行.不练习,缺少体验,技能难以形成,也难以总结.让学生通过操练来获得体验、感受、感悟,并回顾、反思、归纳、总结,形成技能、经验、策略.
遵循规律做事,做任何事都应该有目的.目的不清楚做不好事.如果目的清楚,那就应该围绕目的来进行.教学也是如此,教师做教学,应遵循教学规律、明确教给学生什么.否则,对学生来说则是“照葫芦画瓢”,这是产生“懂而不会、会而不能”现象的根源.
笔者认为,教师非功利性做法是教学生在考场上靠得住、可以迁移到考场上去.概念理解了,知识熟悉了,方法掌握了,思想领会了,用思想串联知识、方法的结构图描绘了,分析问题、解决问题的能力提高了,养成了一个好的解题习惯,学会了思考,这些才是考生在考场上可以依靠的.“算法”,解决一类问题的步骤;“渔”,解一类题的方法,授之以鱼不如授之以渔;“宗”,言有宗,知识方法要有本源宗法,做题要有思想意识主宰.“算法”、“渔”、“宗”、技能、方法、思想、策略、意识等才是可以迁移.相反,别人告诉的不是自己想出来的那些解题过程难以迁移,答案难以迁移,技巧难以迁移等等.如通过求解函数应用问题,概括出解决一类问题的算法:(1)弄清影响函数变动的原因,选择自变量;(2)用自变量的代数式表示函数式中要用到的量;(3)列出函数式,明确定义域;(4)求出最值,并指出相应的自变量值;(5)回答实际问题的解决办法.这个算法不是解决一个问题,而是解决一类问题,是在高考考场上可以依靠的东西.对这些,不能一带而过,要形成文字,要板书,要多次呈现,让学生明确,让学生有抓手.这样,再见到这类问题时,学生就有招了,就知道该怎么下手,也就是“懂而会、会而能”了.
可以这样说,凡是有教育的地方就存在“懂而不会、会而不能”现象.为了消除这种现象,教育家们一直在作孜孜不倦的努力.“学而不思则惘,思而不学则殆”,这是大教育家孔子所思所悟.作为新时代的教育工作者更应与时俱进,充分吸取前人的研究成果,遵循教育规律,勤思教学目的,优化教学流程,力争避免学生“懂而不会、会而不能”现象的发生.
2 把握解题流程、教会学生思考,消除“懂而不会、会而不能”现象
做数学,离不开解题.解题活动应按照波利亚的“怎样解题表”来进行.简短来说,至少做到九个字:“有什么?做什么?怎么做?”.具体说,解题教学过程大致分成三个部分.第一部分:(1)理解题意,明确有什么.(2)分析任务,明确做什么.(3)制定初步解题方案,明确该怎么做.第二部分:实施解题方案.第三部分:回顾反思.这三部分体现在教学流程中,师生该如何做呢?
当前解题教学的现状是:该教师做的教师不专心去做,该学生做的教师抢过来做了.题意理解是轻描淡写,回顾反思是基本不做,“狠做”过程表达.而这个“狠做”也不是第一部分基础之上的狠做,不讲解法产生的思维过程,只是呈现解答,是教师做给学生看.笔者认为,题意理解后面的东西不应该由教师来呈现,教师应该认真做好第一部分,也就是要教会学生面对一个新问题,该怎样读题、审题,该怎样一步一步去分析,该怎样转化等等.但是,分析得好不等于就已经做出来了,要完成解题过程还有很长的路要走.谁去走?应该由学生去走,由他们去实践、经历.在这个过程中还可能出现新情况新问题,教师可以再适时介入,启发、引导,帮助学生克服解题过程中出现的困难,与学生一道走向终点,真正让学生“懂而会、会而能”.“纸上得来终觉浅,绝知此事要躬行”,应让学生经常有“躬行”的机会.
教师当的是导演而不是演员.要多做“技术性强”的活,少干“卖体力”的事.好的教师“想给学生听”,差的教师做给学生看.教师要做好“想给学生听”,就是教学生“学解题”.首先是“学”解题,然后学生才能够自己独立去解题.有学生说“老师讲的我都听得懂,回家后让我自己想就不会了”,这是典型的“懂而不会、会而不能”.怎么“学”解题?怎么消除“懂而不会、会而不能”现象?最好做法是让学生学思考.教师要讲“怎么想到的”、“怎么知道这么想的”才是教学生“学会思考”,才是数给学生回家会想、会做的本领.尤其对那些不善于解题的大多数学生,更要教他们学会思考.不讲“怎么想到的”,原来不会思考的仍然不会思考.要学会思考,怎样“从无到有”,“从不会到会”,“从不能到能”呢?“理解题意”是核心.善于解题的人用一半的时间理解题意,用另一半时间完成解答.学生不能很好解题的最重要原因,是没有树立重视理解题意的意识,没有养成理解题意的良好习惯,更没有掌握如何理解题意的方法.



由 ② ①,得a=2,b=-4,故a+3b=-10.
思维过程能这样充分暴露,是从周期定义出发,遵循的是概念、方法指导思考.概念是思维的细胞,没有概念无法思维.数学思维是抽象思维,是逻辑思维,其特点之一是用概念思考.要养成从基本概念出发,思考和解决问题的习惯.当找到3a+2b=-2时,发现不是整体思想求解,是方程思想在指引你从题中寻找a、b另一等量关系,这是思想指导思考.爱因斯坦说:“不下决心培养思考习惯的人,便失去了生活的最大乐趣.”把数学课上出“数学味”来才能让学生获得乐趣.把思维的教学落到实处,教会学生思考,就是“数学味”.
为了更好地贯彻教会学生思考,消除“懂而不会、会而不能”现象,教师的日常教学要遵循上述合理的解题流程,多讲着手解题的启发性提示语.如:问题是什么?现有什么?还缺什么?它们怎样表示?还能怎样表示?它们有什么关系?它是否与其它问题有联系?能否利用这个联系?等等.往往追问到最后,问到条件与结论的衔接点,思路和方法就自然流露出来了.
教会学生思考,教学还要从学生实际出发.教师要提好问题,提好问题应与学生已有经验相对接,让学生感觉到“你老师能想到的,我差不多也能想到”.让学生与你共鸣,让学生感受过程的自然,否则又是“懂而不会、会而不能”.不要以为,我讲得很清楚,你就应该知道了,掌握了.你讲过了,即便你讲到点子上,但是,到他能够掌握,距离还很远很远.教学任务是什么?是学生“懂而会、会而能”.教师不能着急,着急的一个直接结果就是“告诉”,就是直奔结果,忽视过程,是不讲思维过程的自己说,对学生而言是“夹生饭”,这又是“懂而不会、会而不能”.学习是任何其他人都代替不了的,能够让学生通过自己思考获得,就不要轻易告诉他,这样才能让他“懂而会、会而能”.长此以往,他就学会了如何思考,也就真正获得了如何解决新问题能力.
3 善待通性通法、提炼问题本质,消除“懂而不会、会而不能”现象
当前的另一种现象是迫于高考压力,对常规题、通性通法是拼命讲、拼命练.各地方、各级别的高考研讨会也是同一呼声,认为平时的讲、练、评只能应对偏易、中档试题.难题,是命题人精心设置的创新题,只有依靠学生天生的悟性去解决,对学生能力的培养处于一种消极、被动局面,这是产生“懂而不会、会而不能”现象的另一根源.
在这种认识之下,日常的教学流程是学生先做,老师先改后评,评的是学生做不对的问题,然后再找相似问题,甚至是变换一下数据,再让学生练习,称之为跟踪纠错.对学生做对的问题是视而不见,见了也不知道讲什么,更谈不上如何讲了.不能从学生的思维中准确反思构建问题的本质.长期傻练,学生思维变得呆板、僵化,应变能力弱.此时,通性通法成了学生思维的桎梏,滋长了“懂而不会、会而不能”现象的发生.
新课改已近十年,执行新课改理念应精益求精,不应浮于表面.要把握其精髓,真正落实到平时教学中.《普通高中数学课程标准(实验)》提出了十大理念,其中第七条:“强调本质,注意适度形式化”.在数学教学中,学习形式化表达是一项基本要求,但是不能只限于形式化表达,要强调对数学本质的认识,否则会将生动活泼的数学思维活动淹没在形式化的海洋里.第四条是针对数学思维能力的培养提出,应让学生不断地经历直观感知、观察发现、反思与建构等思维过程.要求教师平时教学要引导学生具体问题具体分析,以通性通法为基础,要力争揭晓数学问题的本质.应在合理发挥形式化作用与揭示数学本质两方面寻求一种动态平衡.
如何揭示数学问题本质?靠回顾反思.反思可以看清问题的本质.“反思性认知”也叫做元认知,是对自己认知的认知.可更加深入地研究.比如,条件分别用在哪里了,各起了什么作用?哪个条件是关键条件?你认为关键的一步是什么?解这类问题的一般步骤是什么?多种解法之间的比较,哪种最好?具有通用性.运用了哪些概念、思想、方法?条件改变一下呢?一般化呢?等等.也就是还要真正设置变式与拓展教学,激活学生思维,才能把反思的东西迁移到陌生的问题中,让学生做到“懂而会、会而能”.
案例2 如图1,在三棱柱ABC—A1B1C1中,BC=CC1,D为AB中点.求证:BC1∥平面A1CD.
通性通法:
法一 如图2,取线段A1B1中点D1,连结BD1、C1D1、DD1,
易证CD∥C1D1,A1D∥BD1,从而平面BC1D1∥平面A1CD⇒BC1∥平面A1CD.


法二 如图3,连结B1C交BC1于P点,易知P点为BC1中点,再取线段A1C中点Q,连结PQ、QD,易证四边形PQDB为平行四边形,则BP∥QD⇒BC1∥平面A1CD.



反思:“你是怎么知道要连结B1C,取线段A1C中点呢?”这一问,方法就能出来.能让学生初步体会平面中的平行线、中位线等与平行有关的定理,在解决立体几何中平行问题的应用,体会“线线平行”、“线面平行”、“面面平行”的相互转化与交融.倘若教学仅停留在通法层面,当学生再做类似问题时,思维肯定还是“云里来、雾里去”,知道怎么做,而无从下手,甚至无功而返,这是“懂而不会、会而不能”的表现.此时教师应就问题的本质继续追问,“要证明BC1∥ 平面A1CD,只要证明BC1平行于平面A1CD内的一条直线就可以了.如图4,哪条直线呢?”联系条件,就是经过BC1与AB的平面与平面A1CD的交线.“交点在哪里呢?”,条件中已有两平面的一个公共点D,只需再找一个公共点,就是连结AC1,线段AC1的中点O就是.这正是应用直线与平面平行判定定理解决问题的本质.评价时,还应该多问一句,“在平面A1CD内,还能找到其它直线与BC1平行吗?”,这样就开阔了学生的思路,发展了思维.实际上,这道题的证明方法很多.
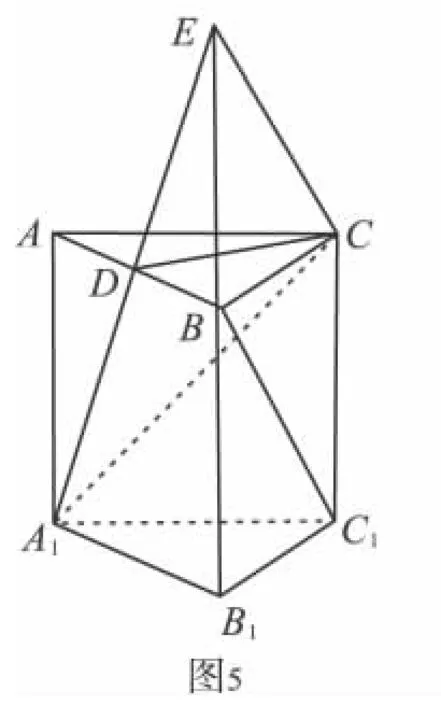
法三 如图5,图中现有一个包含BC1的平面,就是平面BCC1B1.因此画出这个平面与平面A1CD的交线CE,易证明CE∥BC1⇒BC1∥平面A1CD.
法四:如图6,反思经过BC1与AB的平面,关注线段BC1的另一端点,可知经过BC1与A1C1的平面与平面A1CD已有一个公共点A1,“另一公共点在哪儿呢?”这又是一个很有教育意义又具挑战性的问题.通过将三棱柱补成四棱柱易证明A1M∥BC1⇒BC1∥平面A1CD.
这一系列的反思过程,学生感受的是要善待通性通法,要从通法层面寻求新的生长点,要反思问题本质,从多方位、多角度应用直线与平面平行判定定理解决问题,体验的是如何将空间问题向平面转化、如何运用割与补的思想解决问题.这是真正落实了立体几何对学生空间想象能力的的培养.若能做到这样紧扣问题本质教学,学生哪需做那么多习题.只有这样,学生才能从题海中解放出来,才能会一题而能解一类题,进而在考场上才能游刃有余,这才是真正意义上的“懂而会、会而能”.也只有这样,学生才能从数学解题中找到成功的快感,才能热爱数学.体会到不再是数学枯燥乏味,而是数学的魅力无穷.这是消除学生数学学习中“懂而不会、会而不能”现象的最大内驱力.
结束语:教师多一分思考,学生少一分辛劳.消除学生数学学习中“懂而不会、会而不能”现象,改良当前高考复习,提升高考成绩,对每一位高三教师来说是任重而道远.但若能做到教学规律不违背,教会思考做得对,提炼本质常到位,在以能力立意的试题前面,学生才能达到以 “懂而会、会而能”的水平去轻松面对.
1 中华人民共和国教育部制订.普通高中数学课程标准(实验)[M].北京:人民教育出版社,2003
2 王光明、杨蕊.数学学习中的“懂而不会”现象[J].中学数学教学参考,2012、10(上旬)

