“变量分离法”不灵了，怎么办？

安徽省灵璧县灵璧中学 马兆军 （邮编：234200）

有关函数不等式恒成立求参数取值范围的这一热点问题，高考中倍受命题者青睐，这类问题常常作为压轴题进行考查，对考生能力的要求较高，但此类问题解法灵活、综合性强，学生常感到难以下手，通常“变量分离，使不等式恒成立，转化为比最大还大或比最小还小”.但是，近年来相关高考题用变量分离法亦非万能，屡屡难以奏效.变量分离后有时也茫然不知所措，那么到底如何解决这类问题呢？

例1 已知函数f（x）＝x2＋2x＋alnx，当t≥1时，不等式f（2t－1）≥2f（t）－3恒成立，求实数a的取值范围.

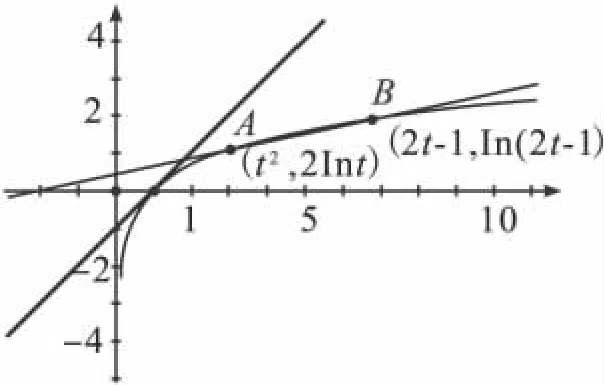
解 当t≥1时，不等式f（2t－1）≥2f（t）－3恒成立，即有（2t－1）2＋2（2t－1）＋aln（2t－1）≥2t2＋4t＋2alnt－3恒成立，（t≥1）.亦即：a［ln（2t－1）－lnt2］≥2［（2t－1）－t2］恒成立.

当t＝1时，不等式显然成立.

当t＞1时，t2－（2t－1）＝ （t－1）2＞0，所以t2＞2t－1＞0，ln（2t－1）－lnt2＜0.

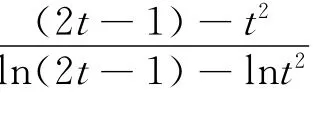
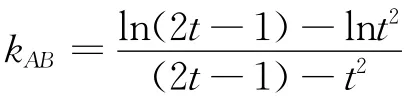
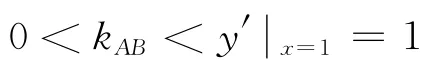
例2 （2010年新课标全国卷第21题）设函数f（x）＝ex－1－x－ax2（Ⅰ）略；（Ⅱ）若当x≥0时，f（x）≥0，求a的取值范围.

此例充分说明，变量分离法仅是求解这类问题的重要方法之一，但有时会使思路走入死胡同，欲解决此类问题还需另辟途径.以例题2为例.（例1也可同法求解.）

解 研究函数f（x）＝ex－1－x－ax2，（x≥0）.注意到f（0）＝0，所以当x≥0时，欲使f（x）≥0，只要函数f（x）＝ex－1－x－ax2在［0，＋∞）上单调递增即可.于是f′（x）＝ex－1－2ax，只要f′（x）＝ex－1－2ax≥0，当x≥0时恒成立即可.又因为f′（0）＝0，则只要f′（x）在在［0，＋ ∞）上单调递增即可.亦即f″（x）＝ex－2a≥0（x≥0）恒成立.而函数f″（x）＝ex－2a≥0（x≥0）在［0，＋∞）上单调递增，故只需f″（x）min＝f″（0）＝1－2a≥0即可，故而a≤时，函数f（x）＝ex－1－x－ax2≥0，（x≥0）恒成立.

从解题过程可知，a≤仅是符合题意的充分条件，是否必要呢？

当a＞时，由f″（x）＝ex－2a＝0，解得x＝ln（2a）＞0，于是函数f′（x）有极小值点，且f′（x）＝ex－1－2ax在［0，ln（2a）］上单减，在［ln（2a），＋∞）上单增 .所以x∈（0，ln（2a）］时，f′（x）＜f′（0）＝0，即f（x）＝ex－1－x－ax2在［0，ln（2a）］上是减函数，所以x∈ （0，ln（2a）］时，f（x）＜f（0）＝0，不符合题意.故而由反证法可知：a≤是当x≥0时，f（x）≥0成立的必要条件.综上所述，a的取值范围是（－∞］.

此法是运用比较法思想，作差与零比较，构造函数h（x），判断函数h（x）的单调性，特别应注意h（0）＝0是否成立？由导函数h′（x）探究h（x）≤0或h（x）≥0恒成立的充分（必要）条件，（有时还需要“用二次”的思路求h″（x）用以判断h′（x）的符号），求出参数的取值范围，然后，再检验该取值范围是否必要（充分）？进而求出h（x）≤0或h（x）≥0恒成立的充分必要条件与参数的取值范围.

再看2012年高考压轴题两例.

例3 （2012年高考天津卷20题）已知函数f（x）＝x－ln（x＋a）的最小值为零，其中a＞0.（I）求a的值.（II）若对任意的x∈ ［0，＋∞），有f（x）≤kx2成立，求实数k的最小值.

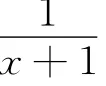
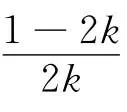
当k≥时，h′（x）≤0，（x≥0）恒成立，h（x）在［0，＋∞）内单调递减，所以h（x）≤h（0）＝0恒成立，即对任意的x∈［0，＋∞），有f（x）≤kx2成立；

当0＜k＜时，h′（x）≥0，（0≤x≤）恒成立，且h′（x）≤0，（x≥）恒成立.所以h（x）在［0］上单调递增，所以h（0）≤h（x）≤h，而h（0）＝0，即存在x0∈ （0，），使得h（x）＞0，不合题意.

综上所述，k≥，k＝.min

例4 （2012年高考安徽卷21题）数列｛xn｝满足x1＝0，xn＋1＝－xn2＋xn＋c，n∈N＊，

（Ⅰ）证明：｛xn｝是递减数列的充分必要条件是c＜0；（Ⅱ）求c的取值范围，使｛xn｝是递增数列.

分析 （Ⅰ）略.（Ⅱ）此题并非不等式恒成立求参数取值范围问题，但是｛xn｝是递增数列时，即：xn＜xn＋1恒成立，于是－xn2＋c＞0⇒0＜xn＜，且0＜xn＜1 －恒成立，（显然变量分离有c＞，易想到c＞ （）max，但是（）max不存在！即使由｛xn｝正项递增数列、上有界，设得：t＝－t2＋t＋c⇒t＝＝F（c）非定值，无法求解c的取值范围.）进而“用二次”思路迭代，探究递归关系，从而求解参数取值范围.解题思路与上同法，求解时思路清晰、流畅，易于掌握.

解 （Ⅰ）略.（Ⅱ）因为xn＋1－xn＝－＋c，所以｛xn｝是递增数列当且仅当－xn2＋c＞0恒成立，且由xn＋1＞x1＝0可知｛xn｝是正项递增数列⇒0＜xn＜，（n≥2）.由n的任意性可知0＜xn＋1＜，所以xn＋1＝－＋xn＋c，满足：0＜－＋xn＋c＜，即－xn－c＋＝（xn－）（xn－1 ＋）＞0，所以0＜xn＜1 －恒成立.即数列｛xn｝的各项取值范围为（0，）∩.

要使｛xn｝是递增数列，由（Ⅰ）知c≥0；若c＝0，则xn＋1－xn＝－xn2≤0，xn＋1≤xn不合题意.又x3＝－＋x2＋c＝－c2＋c＋c＞x2＝c⇒－c2＋c＞0，即要使｛xn｝是递增数列的必要条件是0＜c＜1.

另一方面，xn＋1－＝－xn2＋xn＋c－＝－（xn－）（xn－1 ＋）＝－（xn－）xn＋（xn－）（1 －），注意到－（xn－）xn＞0，所以“用二次”放缩迭代，得到递归关系：

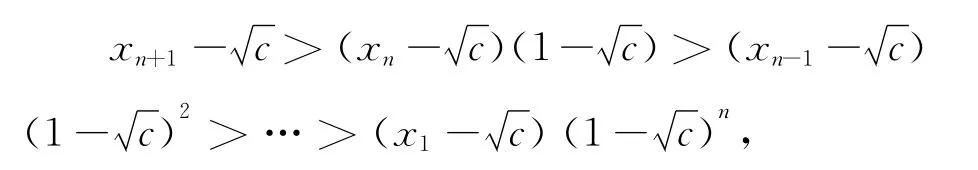
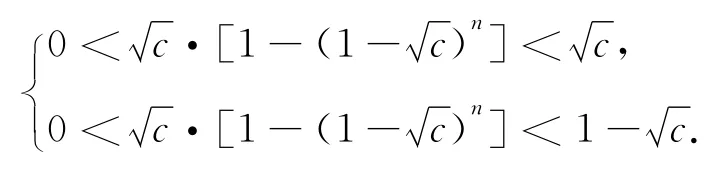
总之，“变量分离法”不灵了，只是一种解题角度的转换.此类问题解法灵活、综合性强，解题时需要认真审题，把探究恒成立问题的充分（必要）条件而构造的函数与变量分离后的相应函数比较，灵活选择适当的方法，进而求解.特别是高考压轴题的求解，要灵活、善变，方法多，思路才会活，难点自然迎刃而解.