基于提高运算求解能力的例题选取

安徽省怀远县包集中学 宋在馥 （邮编：233442）

培养能力，已成为数学教育者的共识和自觉追求.数学能力包括空间想像能力、运算求解能力等六种.而达成这些能力的基础无疑是提高学生的运算求解能力.“运算求解能力是要求会根据法则、公式进行正确运算、变形和数据处理……是思维能力和运算技能的结合……运算能力包括分析运算条件，探究运算方向，选择运算公式，确定运算程序等一系列过程中的思维能力，也包括在实施运算过程中遇到障碍而调整运算的能力.”

培养数学能力的主战场是课堂，而例题是达成教学目标的主要载体，因此例题的选取对实施培养运算求解能力这一目标，显得尤为重要，下面谈谈笔者在教学中为提高运算求解能力，在例题选取方面的思考与尝试：

1 通过例题，引发对基础的重视

例1 己知f（x）＝sin2xsinφ＋cos2xcosφ－sin（＋φ）（0＜φ＜π），图象过点（）.（1）求φ的值；（2）将函数y＝f（x）图象上的各点横坐标缩为原来的，纵坐标不变，得函数y＝g（x）的图象，求函数y＝g（x）在［0］的最大值与最小值.

做法与想法 这是道常规题，没有吸引学生眼球的地方，仅要求对公式、法则等基础知识与方法熟练.若仅仅讲解一遍毫无价值.笔者先让学生自己做，然后小组互查，并就每步的错误做出统计，公布结果.哪知听罢结果令学生目瞪口呆：完全做对的仅有15%，而出现的错误却五花八门.在cos2x降幂、sin＋φ）化简、两角和公式、特殊值求特殊角、横坐标变化与ω的关系、换元法、作图、最值的确定等方面均出现了错误，当告诉学生这是一道12分的高考题，学生变得神情庄重起来，意识到基础知识和基本方法的缺漏和掌握的重要性.以后的课堂采取记公式、特殊值竞赛，疑难问题辩论，建立纠错本等方式以引发兴趣，强化基础.

2 通过例题，强调通性通法

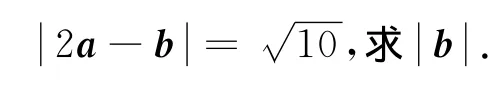
做法与想法 通过学生的尝试得出四种解法：

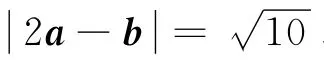
法四 仿法二构造三角形，用平面几何方式求解.

本题的选择，不仅是看重它的一题多解，更看重的是这些解法都是解决向量问题的通性通法，毫无“魔术师”的突然与神奇.但现在的教辅资料里、教师的课堂上却充斥着这样的“突然与神奇”，诱使学生偏离了重视通性通法的轨道，使学生拿到题目便去构想奇思妙解.通过本题的研讨，让学生明白：基础强化了，通法熟练了，攻坚克难便成为了可能.

3 通过例题，学会“翻译”条件

做法与想法 先让学生思考，几乎无人能动笔，原因是视条件为“天书”，这时可引导学生分析运算条件，理解其本质.便设计了以下问题，有了以下问答：

师：f（x1）会在什么范围内？生：在f（x）的值域内（记值域为F）.

师：g（x2）会在什么范围内？生：在g（x）的值域内（记值域为G）.

师：集合F与G有什么关系？

生：（经充分讨论后）得出F⊆G.

师：此题如何解决？

生：分别求出f（x）与g（x）的值域，由F⊆G可求出a.

师：请同学们仿上述条件，给题目重新设置条件，并进行“翻译”.经同学们的反复讨论，教师点拨，得出以下结论：

对于f（x1）＝g（x2）：若∀x1∈［m，n］，∀x2∈ ［a，b］，则F＝G；

若 ∀x1∈ ［m，n］，∃x2∈ ［a，b］，则F⊆G；

若 ∃x1∈ ［m，n］，∀x2∈ ［a，b］，则G⊆F；

若 ∃x1∈ ［m，n］，∃x2∈ ［a，b］，则F∩G≠ ∅.

对于f（x1）≤g（x2）：若∀x1∈［m，n］，∀x2∈ ［a，b］，则f（x）max≤g（x）min.

若 ∀x1∈ ［m，n］，∃x2∈ ［a，b］，则f（x）max≤g（x）max.

若 ∃x1∈ ［m，n］，∀x2∈ ［a，b］，则f（x）min≤g（x）min.

若 ∃x1∈ ［m，n］，∃x2∈ ［a，b］，则f（x）min≤g（x）max.

这些条件的成功“翻译”，使学生信心大增，以后又陆续地给出一些“天书”类的条件，让学生“翻译”，使学生分析条件的能力逐步得以提高.

4 通过例题，学会探究解题的方向

例4 线段AB长为8，点C在线段AB上，且AC＝2，P为线段CB上的一动点，让线段AC、BC分别绕点C旋转，A、C重合于D，设CP＝x，记ΔCPD面积为f（x）.

（1）求f（x）的定义域；（2）求f′（x）的零点.

做法与想法 先让学生试作，几分钟后依然一片寂静，察看结果，仅有几人求出定义域.问其故，有的在求f（x）的解析式上受阻，有的在求导上受阻.复杂的运算、复杂的式子，让学生一片茫然.教师感到已达“愤悱”之境，适时提醒：我们往往忙于出发，常常忘了为什么出发.现在再看看应达到的目的：求定义域与求f′（x）的零点.与学生共同回顾，求定义域的两种情况：给出解析式求定义域与实际问题背景下求定义域，前者只须保证f（x）有意义，后者要满足实际情况.由构成三角形的条件可求出x∈ （2，4）.再问f′（x）零点的几何意义，问题转化为求f（x）的极值点，而CD无限接近于CA和CB时，ΔCPD面积都接近于0，因此在D从A运动到CB上的过程中必有一处使ΔCPD面积达到最大.问题再次转化为求ΔCPD面积最大时的x，因CP＋PD＝6，P点在以D、C为焦点，以6为长轴的椭圆上（为什么想到椭圆，正应了前面讲的“基础熟练，方法自生”）当PD＝PC＝3，x＝3即为f′（x）的零点.解罢此题，同学们深深体会到解题受挫时，常常回顾一下所求结果是什么，往往会启发我们调整解题方向，从而打开解题思路.

培养运算求解能力，应该贯穿整个教学的始终.以上仅是平时教学中尝试的几例，在新课程标准下的教学，既要“仰望星空”（对新课程标准的价值追求），又要“脚踏实地”（从每节课做起，从每道题做起，从每个学生做起，强化基础知识与基本技能），脚步坚实了，我们才能走得更好，走得更远.

1 刘瑞霞.2012年高考数学试题及解法赏析［J］.中学数学教学参考（上旬），2012（7）

2 姜灵灵.抓住本质 回归基础 探究彻底［J］.中学数学（高中版），2012（9）