不变子空间在周期解析信号中的应用*
谭立辉,张志刚
(广东工业大学应用数学学院,广东广州 510006)
1936 年,Armstrong[1]发现在通信信号对正弦信号进行调制,可以有效抑制噪声,人们随之对调频信号中的“频率”这一物理量展开研究。1937年,Carson等人[2]在电路理论中推广了频率的定义,使之成为随时间变化的函数。如果实信号f(t)被描述成ρ(t)cos θ(t)的形式,那么把瞬时频率定义为相位的导数是很自然的,因为它在时间范围内的平均值就是瞬时频率。但我们知道,对于给定的实信号f(t),可以写出很多种形如ρ(t)cos θ(t)的形式,因此如何选取合适[ρ(t),θ(t)]用来定义瞬时频率是当时困扰科学家的一个问题。这个问题直到1946年,才由Gabor[3]引入的解析信号方法得到解决。在此研究的基础上,Ville[4]在1948年给出了一种统一的瞬时频率的定义:
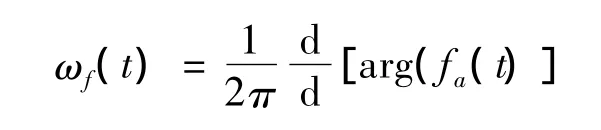
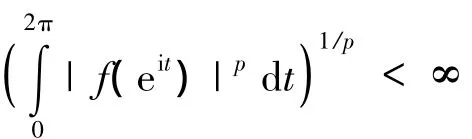
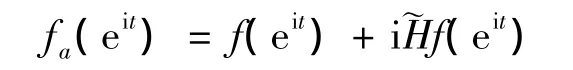
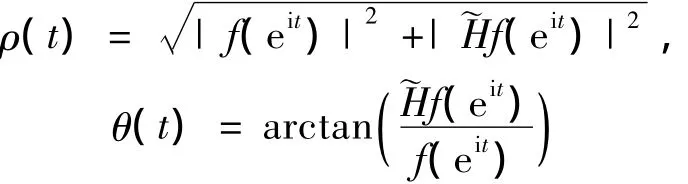
在信号处理中,我们把ρ(t),θ(t)分别称为信号的幅度和相位,ωf(t)=[θ(t)]称为信号的瞬时频率,而称之为共轭周期解析信号。
用解析信号的方法求幅度、相位和瞬时频率已经被广泛地应用于通信和系统鉴定等领域,但用此方法求得的幅度、相位和瞬时频率也存在一些无法合理解释的物理现象,比如说,用解析信号的方法求得的瞬时频率可以不是频谱中的频率之一,解析信号的频谱对于负频率为零,但瞬时频率却可以是负的[5-6]。因此,我们希望求得的相位幅度对[ρ(t),θ(t)]不仅满足等 式[ρ(t)cosθ(t)]=ρ(t)sinθ(t),而且还能进一步满足 Bedrosian等式[7]
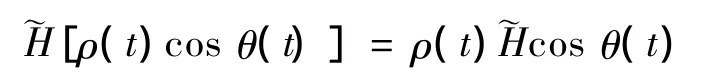
通过对Bedrosian等式的研究,我们发现这个等式成立的一个条件就是周期解析信号与共轭周期解析信号的乘积必须是周期解析信号[8-9]。因此在本文中,我们将利用后移不变子空间的结论,给出周期解析信号与共轭周期解析信号的乘积仍为周期解析信号的充要条件。特别地,当周期解析信号对应的Z变换过圆周解析时,其对应的共轭周期解析信号是有理函数且此有理函数的极点恰为周期解析信号对应的Z变换的零点。作为上述结论的应用,我们研究了具有长度为n的Fourier级数的周期解析信号保持幅度不变的条件。
1 若干引理
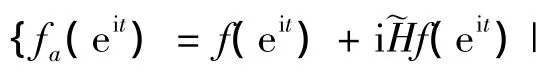
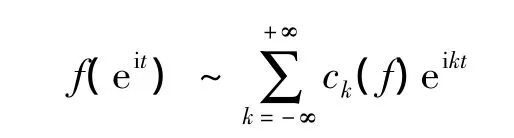
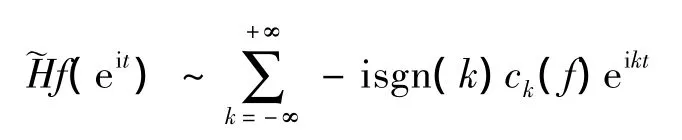
其中sgn表示符号函数,当k≠0,sgn(k)=k/|k|;当k=0,sgn(k)=0。自然周期解析信号具有下面Fourier级数展开形式:

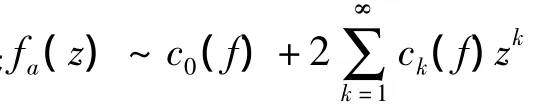
引理1[10]假设不恒等于零的函数f(z)∈aHp(D),1≤p<∞ 。那么对于z∈D,fa(z)有唯一的分解:fa(z)=Ofa(z)Ifa(z),其中Ofa(z)∈Hp(D)是fa(z)对应的外部函数,它能表示成下面的形式
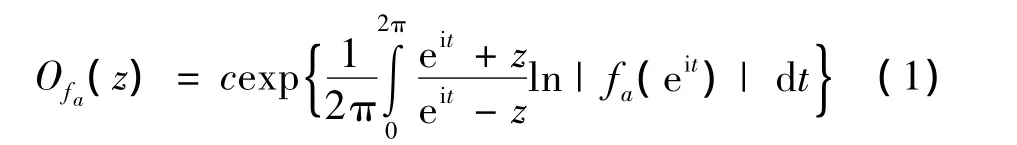
其中c是模为1的复常数;Ifa(z)是其对应的内部函数,它能进一步分解为Ifa(z)=Bfa(z)Sfa(z),其中Bfa(z)是由fa(z)的零点构成的Blaschke积,它可表示为:
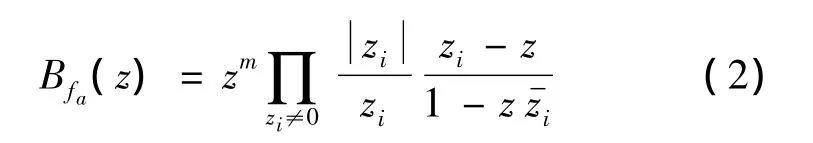
其中 {zi}是fa(z)在单位圆D上的零点序列 (其重点按重数计算),m表示fa(z)在z=0处的重点数,而表示zk的共轭;Sfa(z)是奇异内函数。
显然,对于几乎处处的t∈[0,2π],周期解析信号fa(eit)∈H2[0,2π]可分解为
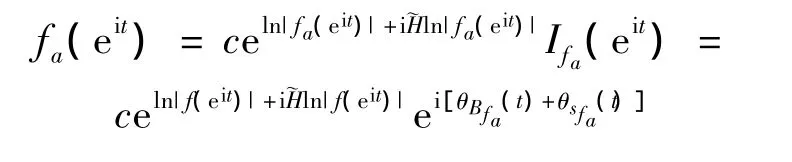
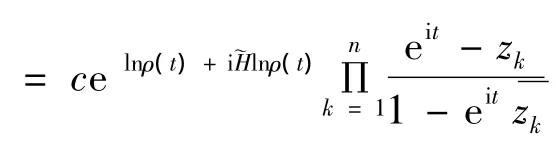
2 主要结论
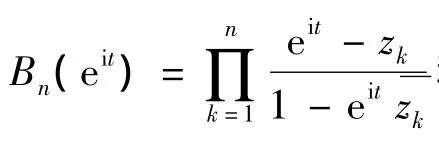
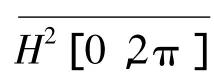
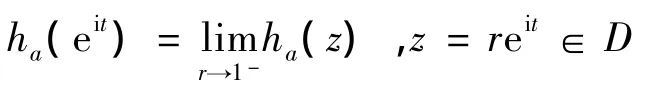
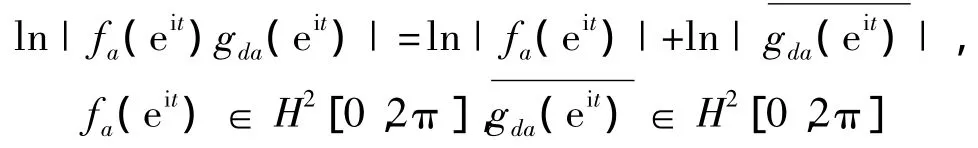
那么,对于几乎处处的t∈[0,2π],有
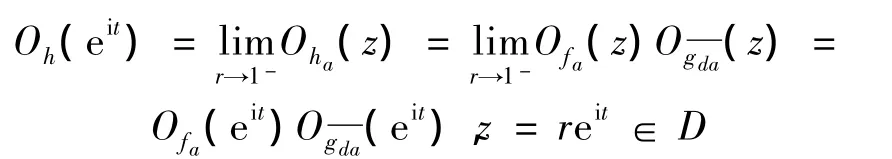
因此,对于几乎处处的t∈[0,2π],有下面的等式成立

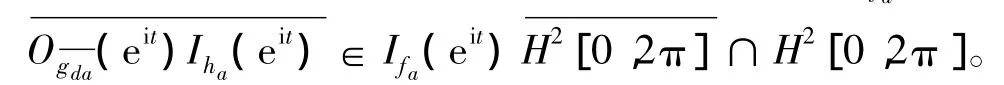
自然,我们有
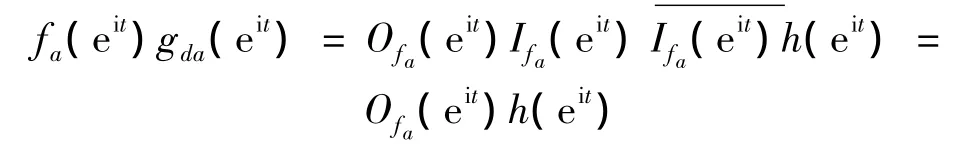
又因为Ofa(eit)∈H2[0,2π],h(eit)∈H2[0,2π],根据 Holder不等式和 F.和 M.Reize定理[10],所以我们有当n<0时,有cn(fagda)=0。
事实上,上述结论已经被我们运用到对Bedrosian等式的刻画中去了[11]。作为上述结果的进一步应用,我们将用它来刻画长度为n的Fourier级数的周期解析信号保持幅度不变的条件。
记Suppf=[inf{n,cn(f)≠0},sup{n,cn(f)≠0}]表示f(eit)∈L2[0,2π]的 Fourier级数支集,令Pm,n[0,2π]表示所有满足f(eit)∈L2[0,2π]且其支集满足 Supp[f(eit)]:=[inf{n,cn(f)≠ 0},sup{n,cn(f)≠0}]⊆[m,n]的函数f(eit)的集合,其中m,n为有限整数。对于Pm,n[0,2π]中的函数,通过简单的计算,我们有以下引理:
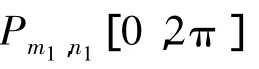
由引理2,定理1和引理3,我们有:
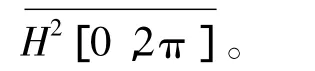
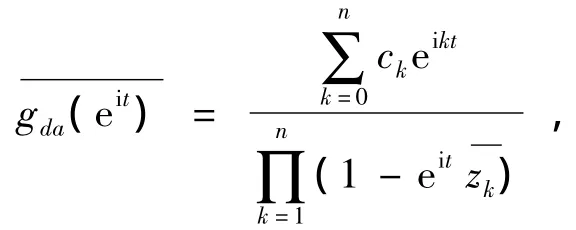
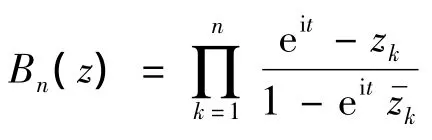
因此存在h(eit)∈H2[0,2π]使得
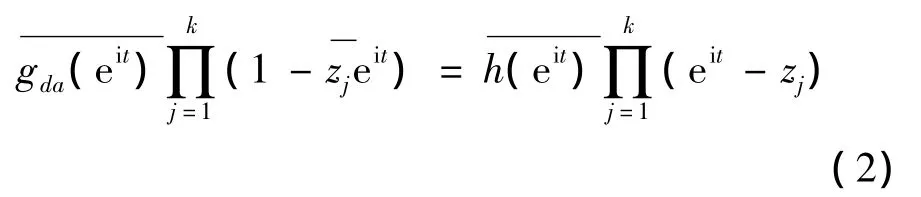
显然地,如果f(eit)∈Pm,n[0,2π],m<0<n,我们知道其对应的解析信号fa(eit)∈P0,n[0,2π]。下面,我们刻画具有有限长Fourier级数的周期解析信号保持幅度不变的条件:
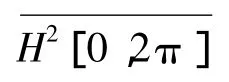
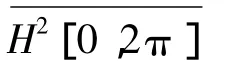
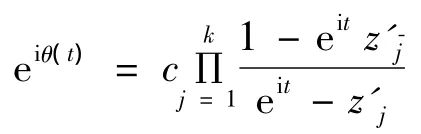
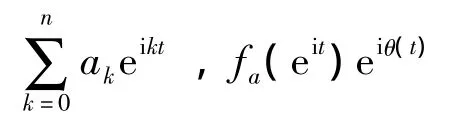
[1]ARMSTRONG E H.A method of reducing disturbances in radio signaling by a system of frequency modulation[J].Proceedings of the Institute of Radio Engineers,1936,24(5):689-740.
[2]CARLSON J L,FRY T C.Variable frequency electric circuit theory with application to the theory of frequencymodulation[J].Bell System Technical Journal,1937,16:513-540.
[3]GABOR D.Theory of communications[J].Journal Institute of Electrical Engineers,1946,93:429 -457.
[4]VILLE J.Théorie et applications de la notion de signal analytique[J].Cables et Transmissions,1948,2:61 -74.
[5]BOASHASH B.Estimating and interpreting the instantaneous frequency of a signal[J].Proceedings of the IEEE,1992,80:520-538.
[6]COHEN L.Time-frequency analysis[M].New Jersey:Prentice Hall,Englewood Cliffs,1995.
[7]HUANG N E,SHEN Z,LONG S R,et al.The empirical mode decomposition and the Hilbert spectrum for nonlinear and non-stationary time series analysis[J].Proceedings of the Royal Society A,1998,454:903-995.
[8]BROWN J.A Hilbert transform product theorem [J].Proceedings of the IEEE,1986,74:520-521.
[9]TAN L H,YANG L H,HUANG D R.Construction of periodic analytic signals satisfying the circular Bedrosian identity [J].IMA Journal of Applied Mathematics,2010,75(2):246-256.
[10]GARNETT J B.Bounded analytic function[M].New York:Academic Press,1987.
[11]TAN L H,YANG L H,HUANG D R.The structure of instantaneous frequencies of periodic analytic signals[J].Science China:Series A,2010,53(2):347 -355.
[12]OPPENHEIM A V,SCHAFER R W.Discrete-time signal processing[M].New Jersey:Prentice Hall,Englewood Cliffs,1989.

