基于DWT的多尺度分块变采样率压缩感知图像重构算法*
蒋业文,于昕梅
(佛山科学技术学院电子与信息工程学院,广东佛山 528000)
由于具有数据的稀疏性表示和高质量信号的恢复性能,压缩感知 (CS)理论目前成为图像采样和图像重构实现的研究热点[1-5]。现实自然图像在某些变换域下几乎总是可压缩的,因此,结合图像统计或结构的先验知识,CS算法如其他信号处理一样能够直接应用于图像数据处理,如图像的采样和重构都可在离散DWT域通过利用小波系数的统计模型来实现[6-7]。
对于图像数据的多维信号处理,CS技术应用的最大挑战是计算的复杂性问题。目前,解决此问题的主要方法是分块CS采样技术,而在重构实现时利用了分块CS的先验知识和平滑投影重构(BCS-SPL)技术[8-9]。相对于图像特征的CS全采样技术,这种方法确实提高了计算开销,解决了计算实时性问题。但是,一定程度上,BCS-SPL技术降低了重构的图像质量。
为了兼顾图像的重构质量和CS的计算开销,借鉴DWT域的BCS-SPL实现技术,本文提出一种新的多尺度分块CS实现技术。与文献 [8]多尺度技术以及文献 [10]通用的全变量TV-CS技术比较,本文的实现方法不但明显地提高了重构的图像质量,而且极大地节约了运行时间。
1 分块CS采样与BCS-SPL技术
CS理论说明,假设信号x∈RN为从M个采样信号中获得的长度为N的信号,且M<<N。那么,我们可以从 (1)式中恢复信号x:

其中,y的长度为M,而A为M×N测量矩阵 (也称为观测矩阵),且具有子采样率S=M/N。如果x在某个变换矩阵Ψ(如DCT,DWT等)下是稀疏的,即有

这里,α为稀疏系数,‖α‖0表示0-范数,即稀疏系数非0的个数。这时,(1)式变为

可以证明[11-12],当测量维数满足K<M<N时,信号x可以通过解决0-范数或1-范数下的优化问题从M=O(KlogN)个测量数据中高概率重构x。
对于一维信号测量矩阵A可采用高斯随机矩阵或伯努利二值随机矩阵等生成。但是,对于二维图像信号,N的长度非常大,如128×128的图像N的长度为104等级。因此,A的计算量很大且难以存储。这样,CS在2D图像中应用受到较大限制。为此,文献 [13]提出一个分块 CS技术(Block-based CS,BCS)。在BCS中,一个图像被分成B×B块,并使用一个近似大小的测量矩阵进行采样。假设xi表示通过Z行扫描输入的第i个图像块的向量表示,那么有

其中,Ф为MB×B2大小的测量矩阵。因此,整个图像的采样子率为S=MB/B2。这时,(1)式中整个图像的测量矩阵A具有对角型结构性矩阵A=diag(Φ),其形式为

这里分块的大小B根据图像重构的速率和重构的质量要求综合决定,按照经验,一般地取B=16,32,64。同时,由于分块之后测量矩阵Ф的维数相对降低,因此,各个块的初始值xi0通过下式可以得到
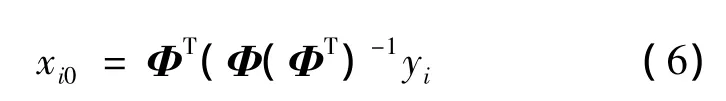
在[5]中,提出的BCS算法中,图像的采样通过分块基的随机矩阵实现,而图像的重构结合平滑滤波器由投影Landweber(PL)算法实现。因此,它的整个实现技术称为BCS-SPL。
BCS-SPL能够实现图像的快速重构,但重构的图像质量取决于分块测量矩阵Ф的具体实现形式。为此,本文基于BCS特性提出一种新的BCS-SPL技术,用以改进图像的重构质量,同时保持图像重构操作的实时性。
2 基于DWT的多尺度BCS-SPL实现技术
2.1 DWT多尺度BCS采样技术
在DWT多尺度BCS-SPL算法研究中,我们把测量矩阵A被分成两个部分:一个是DWT多尺度变换矩阵Ω,另一个是多尺度分块测量矩阵Φ/,即A=Φ/Ω。因此,有

假设Ω为L级DWT分解。那么,在每一级,Φ/组成L个不同的分块采样实现矩阵。这时,图像x的DWT变换形式为Ωx。则,在l级的子带被分成Bl×Bl块,并通过适当大小的矩阵Φl进行采样(其中l=L为最高级分辨率)。
假设是第l级子带s上的第j块图像的向量表示,且满足s∈{H,V,D},1≤l≤L(H表示水平方向子带,V为垂直方向子带,D为对角方向子带)。那么,CS的观测值为

由于不同级的小波分解对图像重构有不同的重要性,因此,本文在每一个l级都会调整采样过程以产生不同的采样子率Sl。其中,设置DWT基带子率为全采样子率,S0=1。
设l级的子率Sl为

这里,Wl为l级的子率加权系数。则,整个图像的采样子率为
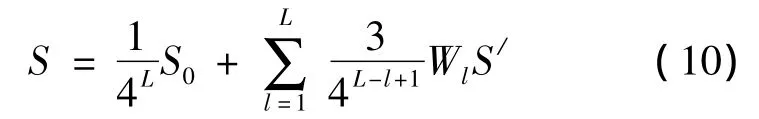
可见,当已知图像的目标采样率S和加权系数Wl后,由 (10)式很容易求出S/,由此再通过 (9)式得到l级的子率Sl。但是,这种处理会产生一个或多个Sl>1的情况。所以,我们必须要对此进行改进并迫使所有l级情况下Sl≤1。由 (9)和(10)式求得S/和S1后,我们检查是否S1>1。如果S1>1成立,设置S1=1,代入 (10)式,可以得到
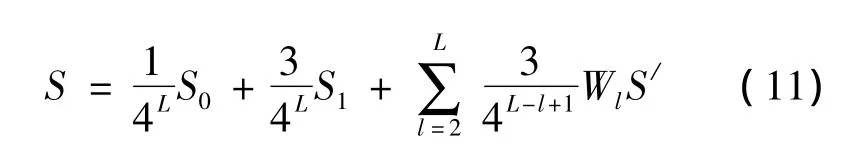
求出S/,再次通过 (9)式重新确定l=2,…,L情况下的子率Sl。重复此过程,直到所有l级情况下Sl≤1。
特别地,经过多次实验,子率加权系数Wl通过下式确定:

表1说明了在各种不同的目标子率下,L=3级DWT变换实现的各级子率统计。
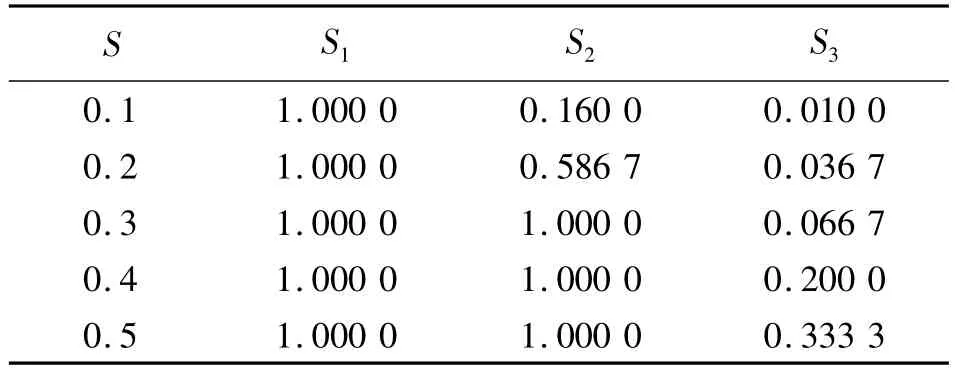
表1 L=3级DWT变换实现的子率统计Table 1 The subrate statistics of three level DWT
2.2 多尺度BCS图像重构算法
在图像DWT稀疏变换域内,结合图像边缘的3×3维纳滤波和稀疏提升阈值处理,表2说明了本文多尺度BCS图像重构实现算法的流程。其中,维纳滤波在空间域实现,而平滑和阈值操作在变换域进行,Landweber实现步骤形式为x←x+ΦT(y-Φx)。实现时,在DWT分解的每一级中的每个块都使用了适当大小的Φl采样矩阵和Landweber迭代步骤。

表2 多尺度BCS 2D图像重构算法Table 2 The 2D image reconstruction algorithm based multiscale BCS
3 实验结果
对512×512的几幅灰度图像进行基于DWT的多尺度BCS采样并且重构,同时与文献 [8]提出的BCS-SPL算法、文献 [10]提出的TV算法以及文献 [9]描述的多尺度GPSR算法进行比较。其中,本文算法和 BCS-SPL算法均使用双树DWT(DDWT)作为稀疏基Ψ,采样时使用9/7双正交3级DWT作为多尺度变换矩阵Ω。Ω进行l级分解时,大小为Bl×Bl图像块采样使用文献 [11]提出的随机DCT SRM观测矩阵进行实现。而TV算法使用文献 [10]的扰乱块Hadamard SRM作为观测矩阵,多尺度GPSR算法使用Gaussian尺度混合模型进行采样。其他实验条件相同。当l=1,2,3时,块的大小分别为Bl=16,32,64,每一级的采样子率都使用表1的计算结果。图1说明了几种算法重构Lena图像的部分实验结果。由图可见,当采样子率S=0.1时,本算法提出的小波域分块采样和多尺度重构的图像质量优于BCS-SPL算法约3 dB。同时,本算法也优于TV算法和多尺度GPSR算法约1-2 dB。表3说明了几种算法对Lena图像、Barbara图像以及Pepper图像重构质量(以PSNR为衡量标准)的对比结果。某些情况下,当采样子率较高时,对于重构的Barbara图像,TV算法性能优于其它算法。但是,TV算法的实时性能最差。
4 结论
在DWT域内,利用分块CS采样技术,本文提出了一种图像多尺度分块压缩感知采样与重构图像算法。相比BCS-SPL算法,由于本文的算法在DWT每级分解的每个子带上都使用多尺度重构Landweber技术并结合了维纳滤波技术,使重构的图像质量大约提高了1~3 dB。同时,本文的算法降低了实现的复杂性,并具有较高的实时性能。相对于常用的DWT图像处理算法,由于分块CS图像处理算法在每个子带上利用了DWT的多分辨率和多尺度特性,所以,其观测结果能充分表示图像的内部结构。因此,本文提出的算法重构的图像质量也更好,且需要的数据量更少。但它比常用的DWT图像处理算法复杂性要高,且实时性较差。这也是提高图像重构质量带来的必然结果。未来,我们将进一步研究该算法对图像特征采样的稀疏性和实现的有效性。

图1 CS图像重构算法的实现比较 (S=0.1)Fig.1 The performances comparison based CS image reconstruction algorithm

表3 几种算法重构图像的PSNR(dB)对比结果Table 3 Comparison Results of PSNR(in dB)for several image reconstruction algorithm
[1]CANDES E,ROMBERG J,TERENCE TAO.Robust uncertainty principles:Exact signal reconstruction from highly incomplete frequency information[J].IEEE Trans On Information Theory,2006,52(2):489 -509.
[2]DONLHO D L,TSAIG Y.Extensions of compressed sensing[J].Signal Processing,2006,86(3):533 -548.
[3]CHEN C,TRAMEL E W,FOWLER J E.Compressed-Sensing recovery of images and video using multihypothesis predictions[C]∥Proceedings of the 45th Asilomar Conference on Signals,Systems and Computers,Pacific Gro-ve,CA,2011:1193-1198.
[4]杨海蓉,张成,丁大为,等.压缩感知理论与重构算法[J].电子学报,2011,39(1):142 -147.
[5]练秋生,周婷.结合字典稀疏表示和非局部相似性的自适应压缩成像算法[J].电子学报,2012,40(7):1416-1422.
[6]KIM Y,NADAR M S,BILGIN A.Compressed sensing using a Gaussian scale mixtures model in wavelet Domain[C]∥Proceedings of the International Conference on Image Processing,Hong Kong,2010:3365 -3368.
[7]周燕,张德丰,马子龙.基于压缩传感的图像哈希水印算法[J].中山大学学报:自然科学版,2010,49(6):58-63.
[8]MUN S,FOWLER J E.Block compressed sensing of images using directional transforms[C]∥Proceedings of the International Conference on Image Processing,Cairo,Egypt,2009:3021 -3024.
[9]SCHNITER P,POTTER L C,ZINIEL J.Fast bayesian matching pursuit:Model uncertainty and parameter estimationfor sparse linear models[J].IEEE Transactionson Signal Processing,2009,57(3):2201-2229.
[10]CANDES E,ROMBERG J,TERENCE T.Stable signal recovery from incomplete and inaccurate measurements[J].Communications on Pure and Applied Mathematics,2006,59(8):1207 -1223.
[11]DO T T,TRAN T D,GAN L.Fast compressive sampling with structurally random matrices[C]∥Proceedings of the International Conference on Acoustics,Speech,and Signal Processing,2008:3369-3372.
[12]赵慧民,郭一缜,丁晓艳,等.用于视频多播传输的压缩传感实现方法研究[J].中山大学学报:自然科学版,2012,51(1):45-49.
[13]GAN L.Block compressed sensing of natural images[C]∥Proceedings of the International Conference on Digital Signal Processing,Cardiff,UK,2007:403 -406.

