基于奇异值分解的桥梁挠度分离研究*

刘夏平，杨 红，孙 卓，杨 坚，刘爱荣

(1.广州大学土木工程学院，广东广州 510006;2.广州大学物理与电子工程学院，广东广州 510006)

挠度是评定桥梁结构安全与否的关键参数，桥梁挠度变化客观反映出桥梁在各种荷载及环境作用下的工作状态和自身材料的变异。由于通过传感器监测得到的桥梁结构挠度通常是由车辆、人群等荷载，以及环境因素等综合作用下的总效应，因此，精确获取挠度监测信号各响应分量，是正确诊断桥梁结构病害、准确评估其工作状态，以及分析病害发生机理的前提和基础［1－2］。

针对桥梁结构挠度信号分离，目前已有部分学者开展了相关研究，如梁宗保［3］采用小波多尺度分析手段研究了活载挠度分离的方法;陈德伟［4］研究了神经网络方法在提取温度挠度方面的应用;刘夏平［5］提出了一种基于最小二乘支持向量机方法的日温差挠度和年温差挠度的分离方法。Sohn H［6］研究了自联想神经网络方法在剔除温度效应影响中的应用;刘纲［7］研究了粒子群优化算法在日温差挠度效应分离中的应用。由于桥梁挠度信号分离是工程界一个崭新的研究领域，相关研究处于起步阶段，目前在挠度分离手段上尚较少，一些分离方法在精确性、稳定性和实用性方面还存在不足，因此开展桥梁挠度分离方法研究十分必要。

奇异值分解是线性代数中一种重要的矩阵分解，是矩阵分析中正规矩阵酉对角化的推广，在信号处理、模式识别、数据压缩等领域有重要应用［7－10］。本文针对桥梁挠度监测信号中日温差挠度与年温差挠度通常具有周期性的特点［11］，采用奇异值分解提取周期信号的盲分离方法，利用桥梁结构挠度信号分量的周期性实现挠度监测信号各成分的精确分离。

1 理论框架

1.1 挠度信号模型

安装在桥梁上的单个传感器接收到的是来自多个信源交织在一起的挠度信号流S(t)，其中主成分有荷载挠度信号S0、日温差挠度信号S1、年温差挠度信号S2、骤然降温挠度信号S3、长期挠度信号S4(包括混凝土收缩徐变挠度、预应力损失及结构损伤等的挠度效应)，以及环境噪声和系统的测试误差S5等，即

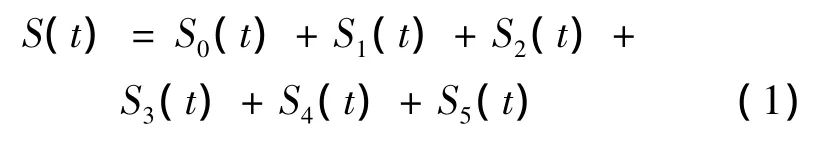
式 (1)中主成分各分量之间，一般可认为是不相关的。对接收信号进行无失真采样，则其离散形式为:

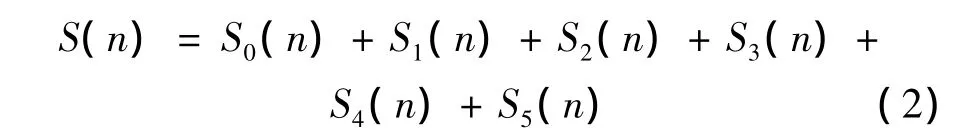
由于活荷载效应分布在信号的高频部分且与其他挠度成分频率差别较大，故借助低通滤波手段可剔除活荷载效应;此外，可以采用滤波方法消除高频噪声信号，或根据挠度监测信号中有用信号和噪声时频特征的不同，利用小波变换将含噪信号进行多尺度分解，然后在每一个尺度层上把属于噪声的小波系数去除，保留并增强属于信号突变的小波系数，最后利用小波重构算法恢复信号［12］，以此消除噪声干扰。因此，式 (2)可写成以下形式

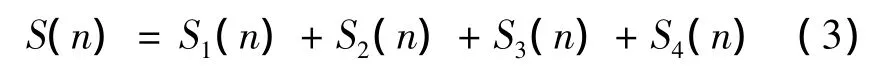
1.2 奇异值分解

设有N行M列的实矩阵A，对它可以做如下的分解，称之为奇异值分解［13］。

式中，U=［u1，u2，…，um］∈Rm×m，UTU=I;V=［v1，v2，…，vn］∈Rm×m，VTV=I;m×n维矩阵∑为［diag(δ1，δ2，…，δp)∶0］或其转置形式，取决于m＜n还是m≥n，p=min(m，n)，δ1≥δ2≥，…δp≥0。δ1，…δp称为矩阵A的奇异值，非零奇异值包含了矩阵A的有用信息，δi对应的列向量ui和vi分别称为第i个左奇异向量和第个右奇异向量。Ai(uiδivi)仍然是一N行M列矩阵，于是将矩阵A展开成如下形式

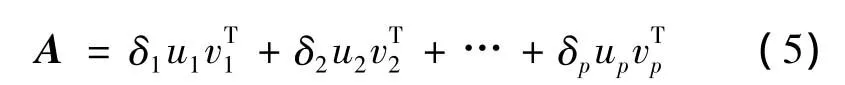
同时将该矩阵A和A1各行首尾相接分别得一维向量S和xi，则式 (5)又可写成如下形式

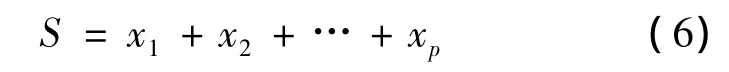
由式 (6)可知，原始信号是所有分量信号的简单线性叠加，从原信号中分离一个分量信号的过程就是从原信号中减去该分量信号，从而使得分离出来的各分量信号保持它们在原信号中的相位不变，即具有零相位偏移特性。

1.3 挠度信号矩阵构造及其分离模型构建

设有一组通过安装在桥梁结构上的单个传感器采集到的桥梁挠度信号，按式 (3)的信号模型分析可知，该桥梁挠度信号包含日温差效应信号、年温差效应信号以及长期挠度信号。利用先前已获知的日温差效应信号周期长度，将该桥梁挠度信号构造成如下矩阵

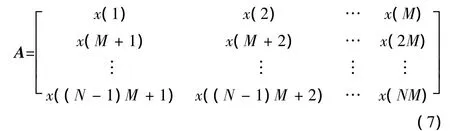
对A进行奇异值分解，将u1δ1v1矩阵各行首尾相接近似恢复挠度信号中日温差效应信号S1，从S中剔除S1部分，即S′=S－S1。将S′再按年温差效应信号周期长度M1分段，构造如下矩阵

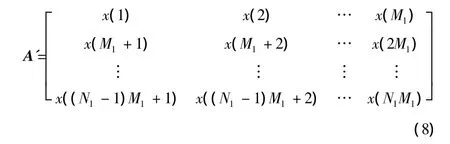
同样对 A′进行奇异值分解，通过u′1δ′1v′1矩阵各行首尾相接近似恢复年温差效应信号S2，从S′中减去S2成分，即得到其余挠度成分。

2 挠度模拟信号分离

2.1 挠度模拟信号

以一座三跨预应力砼连续刚构桥为背景桥梁，采用有限元进行仿真分析，获取各挠度成分信号。

背景桥跨径组合为65 m+100 m+65 m，预应力砼连续刚构体系。采用Midas/Civil软件计算主桥中跨挠度值为:整体升温1℃，跨中挠度f′=1.5 mm(上拱);截面线性升高温差1℃，跨中挠度f″=－1.5 mm(下挠)。取每天的整体日温差幅值为10℃，截面温差为5℃，年温差为35℃，因日温差和年温差为周期性函数，假设其按正弦变化，则可得到按时序变化的日温差效应S1和年温差效应S2。假设长期挠度由混凝土收缩徐变因素导致，采用《公路钢筋混凝土及预应力混凝土桥涵设计规范》(JTG D62－2004)可计算该桥梁收缩徐变效应S3。因此，跨中总挠度S(t)可按下式计算［5］:

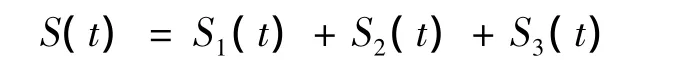
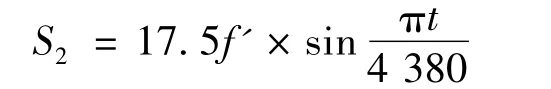
上式采样频率为1次/h，挠度单位为mm，模拟的挠度时程曲线如图1所示，图2为所有模拟挠度组成的混合模拟挠度时程曲线。

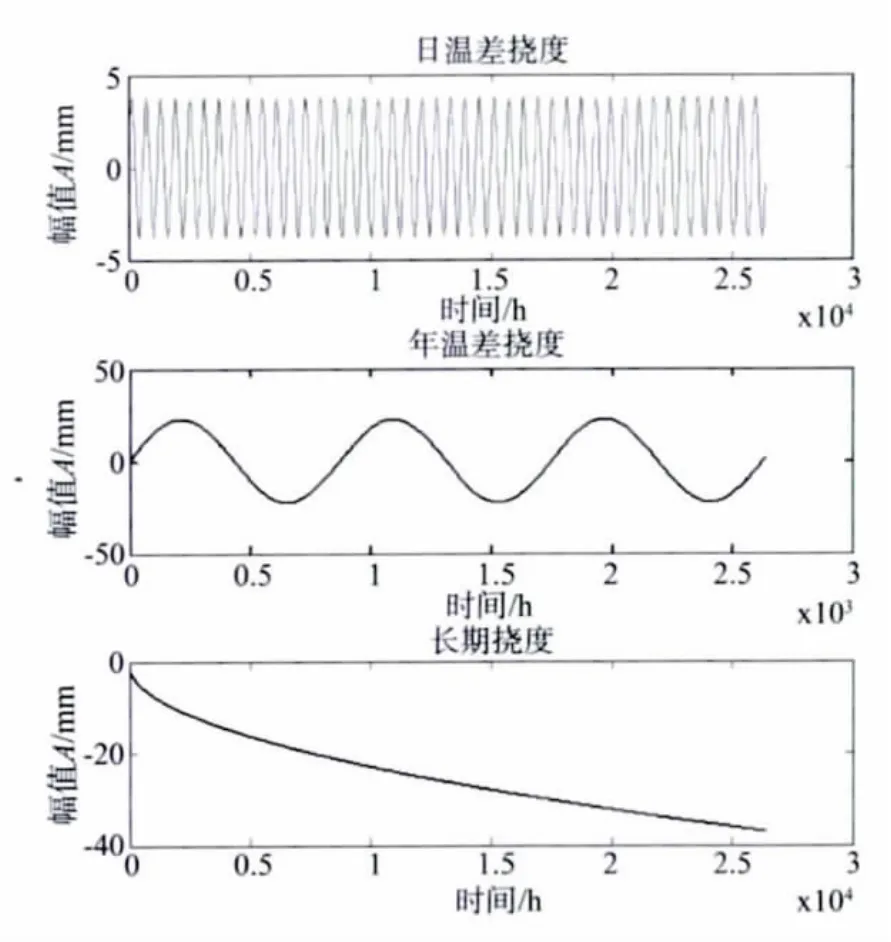
图1 模拟的挠度时程曲线Fig.1 Simulating deflection history

2.2 模拟挠度的分离

图2 混合的模拟挠度时程曲线Fig.2 Mixture values history of simulating deflection

对混合的模拟挠度进行奇异值分解，得到图3所示的各挠度成分时程曲线。与图1比较可看出，分离得到的各挠度成分时程曲线与原始时程曲线波动规律非常相似。表1为分离值与实际值相关系数和相对误差，从表中可看出各挠度成分的相关系数在0.900～0.999之间，相对误差均值在0.001～0.024之间，相对误差均方差在0.01～0.1之间，分离效果良好，特别是具有周期信号特征的温度挠度相关系数均在0.95以上，相对误差均值在0.003以下，相对误差均方差在0.027以下，分离效果较精确。

图3 分离后的模拟挠度时程曲线Fig.3 Separation values of simulating deflection history

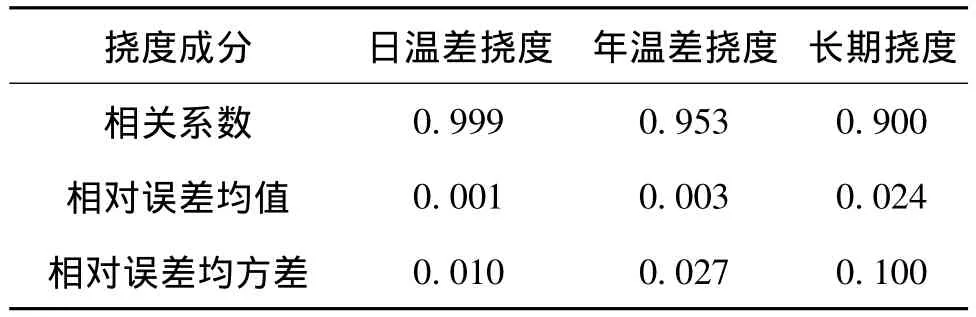
表1 模拟挠度分离值与实际值相关系数和相对误差Table 1 Separating simulating deflection correlation coefficient and relative error

3 挠度实测信号分离

3.1 挠度实测信号

为了获取桥梁结构真实的挠度信号，本文在2012年7月17日18:00～19日18:00，对广东佛山市潭州大桥扩建桥进行了48 h的连续现场温度场观测和挠度监测。潭洲大桥位于佛山莲塘水闸下游的潭洲水道，该桥扩建桥梁主桥采用75 m+125 m+75 m预应力混凝土连续刚构箱梁桥 (见图4)，桥梁宽14.25 m(包括1.75 m人行道)，箱梁采用单箱单室截面，墩身采用薄壁空心墩，墩身截面采用单箱单室结构，墩身纵桥向宽2.8 m，横桥宽7.25 m。设计荷载:公路－Ⅰ级;设计速度:120 km/h。目前已基本完工，待开放交通。

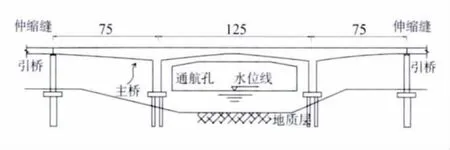
图4 潭洲大桥立面图 (m)Fig.4 Elevation of Tan Zhou bridge(m)

挠度监测采用BJQN－5B型动挠度仪，该仪器采用无线遥控靶标，实现自动标定动态测量，分辨率为测量量程的0.1%，测量精度为±0.02 mm，最大采样频率为300 Hz。试验时实际采样频率为10 Hz。

挠度实测时域曲线如图5所示。

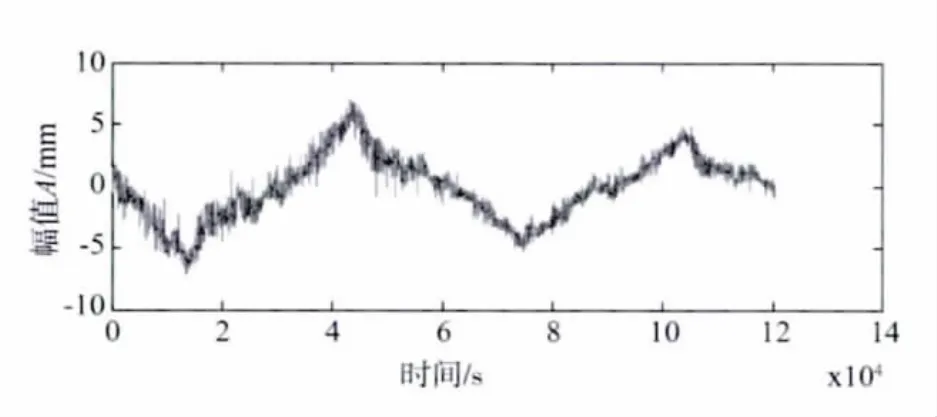
图5 实测挠度时程曲线Fig.5 Actual deflection history

由于该桥建成后尚未通车，且监测时间相对较短，挠度监测结果中可以忽略混凝土徐变收缩等产生的影响，认为挠度主要由环境温度变化以及环境噪声所引起。

由于环境噪声和其它因素存在，采用滤波技术手段对实测温度挠度进行滤波，滤波后的温度挠度时程曲线如图6所示。

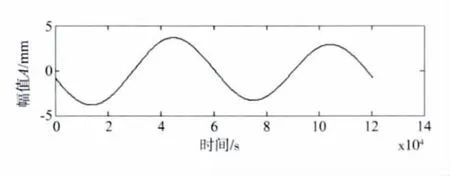
图6 滤波后的实测挠度时程曲线Fig.6 Actual deflection history after filtering

3.2 骤降温差挠度

为了研究奇异值分解在实际工程挠度成分的分离效果，考虑到两天时间内有可能出现骤然降温，因此，采用有限元进行骤然降温仿真分析，获取骤降温差挠度，并与实测挠度组成混合信号。

采用Midas/Civil专业软件建立潭州大桥扩建桥主桥有限元计算模型，共建立99个节点，96个梁单元，并对其进行结构计算分析，计算结果显示，整体降温1℃时，跨中挠度为－1.48 mm(下挠)。选取直线和二次曲线模型分别模拟骤降温差，按两天内骤降温度5℃考虑，据此计算得到骤降温差作用下跨中挠度的时程曲线如图7所示，与实测挠度混合后并经过均值化处理的时程曲线分别如图8(a)(骤降温差为直线模型)和图8(b)(骤降温差为二次曲线模型)所示。

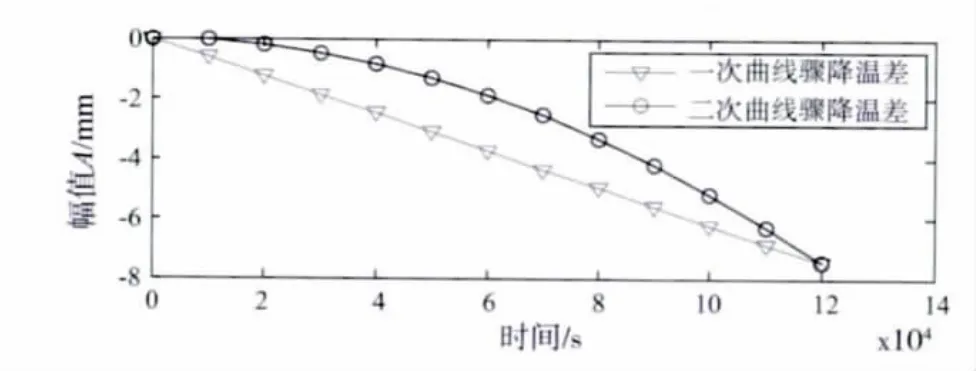
图7 骤降温差挠度时程曲线Fig.7 Deflection history of temperature plummeted

3.3 实测挠度的分离

对图8(a)和图8(b)的挠度混合信号进行分离，分离出的日温差挠度如图9(a)(骤降温差为直线模型)和图9(b)(骤降温差为二次曲线模型)所示;与图6的实际值比较，得到各挠度成分的相关系数和相对误差如表2所示，从表中可看出，相关系数均在0.900以上，相对误差均值在0.004以下，相对误差均方差在0.031以下，实测温度分离效果也很好，特别是当骤降温度挠度为直线时，分离的日温差挠度相关系数很高，相对误差较小;当骤降温度挠度为二次曲线时，分离效果稍差些。

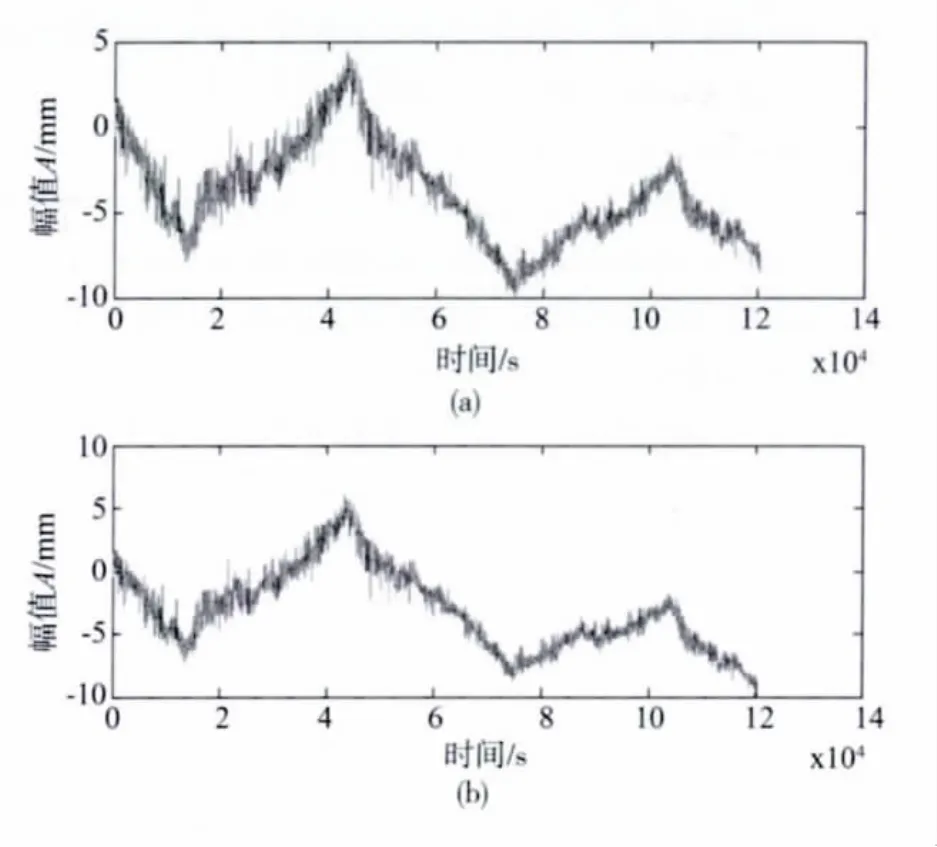
图8 混合挠度时程曲线Fig.8 Mixture values of deflection history

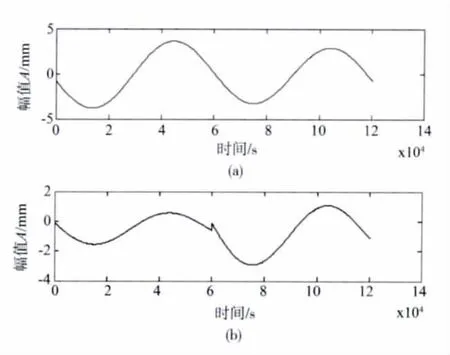
图9 分离后的实测挠度时程曲线Fig.9 Separation values of actual deflection history

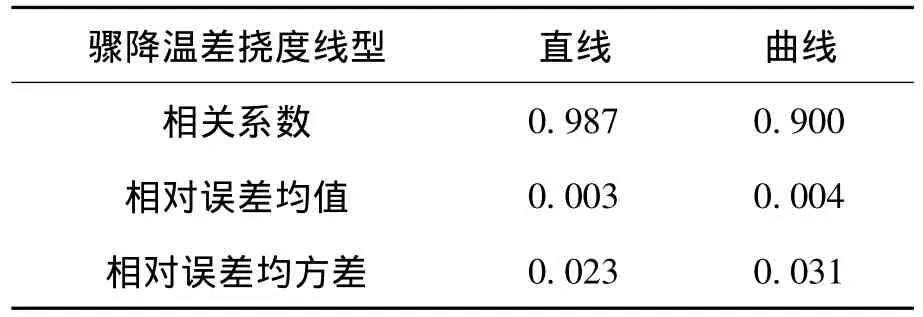
表2 实测挠度分离值与实际值相关系数和相对误差Table 2 Separating actual deflection correlation coefficient and relative error.

4 矩阵构造对分离效果的影响

将奇异值分解应用于桥梁结构挠度分离的关键，是如何利用信号序列构造出合适的矩阵。通过对信号的连续截断来构造矩阵时，通常按信号周期T整倍数截取数据长度。为了研究截取数据长度对分离效果的影响，针对前述桥梁挠度模拟信号，日温差挠度周期T为1日，采样频率为每小时1次，每1个周期T的数据长度为24个数据，每次分别连续截取 (1+Δt)T(其中 Δt=0，0.1，…1)内的数据长度构造矩阵，进行奇异值分解，得到日温差挠度的相关系数如图10所示。从图中可看出，构造矩阵时截取的数据长度对分离效果有明显的影响，当截取1T、1.5T及2T的数据长度构造矩阵时，相关系数最大，因此，以信号周期T的0.5倍数截取数据长度构造矩阵分离效果最好。

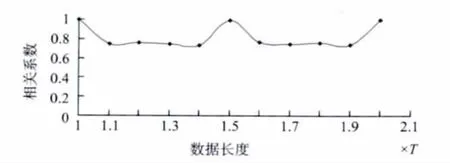
图10 数据长度－相关系数曲线Fig.10 Data length-correlation coefficient curve

5 结论

本文针对桥梁挠度分离问题，基于奇异值分解原理，提出一种挠度各分量精确分离的方法，实现了挠度准确分离。主要结论如下:

1)模拟信号及实测信号计算分析结果表明，基于奇异值分解的挠度分离，分离值与实际值相关系数均在0.900以上，相对误差均值在0.004以下，相对误差均方差在0.1以下，是一种较精确的分离方法;

2)具有周期信号特征的温度挠度，模拟信号分离的相关系数均在0.953以上，实测挠度与线性骤降温差挠度分离的相关系数达到0.987，相对误差均在0.024以下，相对误差均方差在0.031以下，因此，奇异值分解提取信号的方法对分离具有周期性的桥梁挠度温度效应特别有效。

3)构造矩阵时截取的数据长度对分离效果有明显的影响，以信号周期的0.5倍数截取数据长度构造矩阵时，分离值与实际值相关系数最大，分离效果最好。

［1］KENT K S，TERRY P，JUAN C A，et al.Failure of concrete T-beam and box-girder highway bridges subjected to cyclic loading from traffic［J］.Engineering Structures，2010，32(7):1838 －1845.

［2］RICHARD W B F，CHRISTOPHER H，SENTURK A E.Experimental and analytical evaluation of reinforced concrete girders under low-cycle shear fatigue［J］.Structural Journal，2010，107(2):199 －207.

［3］梁宗保.基于监测信息统计分析的桥梁结构安全评价研究［D］.重庆:重庆大学，2006.

［4］陈德伟，荆国强，黄峥.用人工神经网络方法估计桥梁在温度作用下的挠度行为［J］.结构工程师，2006，04(5):24－28.

［5］刘夏平，杨红，孙卓，等.基于LS-SVM的桥梁挠度监测中温度效应分离［J］.铁道学报，2012，34(10):91－96.

［6］SOHN H，WORDEN K，FARRAR C R.Statistical damage classification under changing environmental and operational conditions［J］.J Intel Mater Syst Struct，2003，13:561－574.

［7］KANJILAL P，PALIT S.On multiple pattern extraction using singular value decomposition［J］.LEEE Transactions on Signal Processing，1995，43(6):1536－1540.

［8］KANJILAL P，PALIT S.The singular value decomposition——applied in the modellingand prediction of quasiperiodic processes［J］.Signal Processing，1994，35(3):257－267.

［9］赵学智，叶邦彦，陈统坚.矩阵构造对奇异值分解信号处理效果的影响［J］.华南理工大学学报:自然科学版，2008，36(9):86－93.

［10］唐冬，张广驰，张琳，等.基于几何均值分解的MIMO系统误码率性能分析［J］.中山大学学报:自然科学版，2007，46(1):40 －47.

［11］刘纲，邵毅敏，黄宗明，等.长期监测中结构温度效应分离的一种新方法［J］.工程力学，2010，3(10):55－66.

［12］涂建成，席旭刚，罗志增.一种改进阈值的平移不变量小波消噪方法［J］.信息与控制，2011，2(40):150－154.

［13］GOLUB G H，V AN LOAN C F.矩阵计算［M］.袁亚湘，译.北京:科学出版社，2001.