河流冲刷作用下人工堤岸稳定性研究*
刘 动,陈晓平,黄井武
(1.暨南大学理工学院,广东广州 510632;2.暨南大学重大工程灾害与控制教育部重点实验室,广东广州 510632;3.广东省水利电力勘测设计研究院,广东广州 510170)
人工堤防是约束河势、防御洪水的重要屏障,其稳定性取决于两方面因素,一是堤防断面的设计和堤身、堤基材料特性,另一是堤坝在各种荷载作用下的响应,包括河流冲刷力、渗透压力、自重压力等,其中近岸水流对堤脚和堤岸的冲刷现象在我国25万km的各类堤防上十分普遍,由冲刷导致的堤坝稳定方面的问题也时有发生,特别是一些填筑质量不高的堤防。另外,水流冲刷作用造成的河床下切及深槽迫堤情况也对堤防的稳定构成极大威胁。鉴于工程失稳的严重后果,河流冲刷作用下的堤防稳定性问题一直受到政府和相应技术部门的高度重视。
河流冲刷下堤岸稳定状态反映水与堤岸 (堤脚)结构相互作用的过程和结果。对于人工堤岸,河流冲刷将造成堤脚几何形状的改变,并因此改变水流边界条件;边界条件的改变反过来影响河势,进而通过河势的变化影响堤防,这种演变过程一直在平衡与不平衡之间延续,其力学过程涉及多学科知识,是研究中的难点。
本文选择广东北江西南镇河段为研究对象,对冲刷作用下堤岸及河床几何形状改变进行预测,在此基础上提出了了平面水动力学-土力学堤岸稳定耦合分析方法,探讨河流冲刷对堤岸稳定性和变形的影响。
1 堤岸及河床演变与预测方法
冲刷作用下堤岸及河床变形演变的过程非常复杂,涉及的因素也是多样的,但归根到底是水流、沙和岸坡相互作用的结果。目前研究堤岸变形演变的方法主要有[1-3]:① 模型试验方法,此方法主要针对重大水利工程,由于水、沙相互作用的模拟非常复杂,要求投入成本较高,且需要较多人力和物力支持。②数学模型方法,利用数学方法建立模型,模拟水、沙和岸坡的作用过程,成本少、研究方便,但由于水、沙、边界问题的复杂性,数学求解较困难,无法预测冲刷过程的各种随机因素,且对某些特殊的堤岸变形无法模拟和预测。③实测资料分析法,对于一般工程问题,常利用此方法进行定性的推理分析,利用已有监测数据预测后期岸坡的演变。
堤岸变形演变是一个复杂的非线性动态系统,其演变的实质是水、沙和岸坡的相互作用,不断调整的结果,而人工神经网络模型具有的较强非线性映射能力、较高的容错性、较广的适应能力,都十分适合非线性问题的研究,因此可以说用人工神经网络方法来研究堤岸的演变和预测是非常合适的。本文利用人工神经网络方法对堤岸及河床变形进行了定量的预测分析,得到河流冲刷后堤岸坡脚的几何形态,作为探讨河流冲刷作用下的堤岸稳定性的重要前提。
1.1 人工神经网络模型的影响引子的分析
水流冲刷下堤岸及河床的变形主要取决于近岸水流的冲刷能力和堤岸的抗冲能力。水流的冲刷能力体现在冲刷作用对堤岸及河床的影响,堤岸冲刷根据控制条件分为冲积作用和非冲积作用,前者指水流直接冲刷和重力作用下的坍塌,后者指其他外界条件造成河岸土体被淘刷和强度减小造成的坍塌,天然条件下两种作用同时控制着河岸的冲刷过程,其中水流的冲积作用是主要的控制因素[4]。水流的冲刷能力概括成对堤岸及河床的影响引子主要包括:上游来水量 (Q),来水变化规律,上游输沙量 (S),输入沙量的变化规律,及泥沙组成等因素。仔细分析上述因素,可以发现一般河流的冲刷和淤积过程多是由底沙输送方式完成的,而来水变化规律和输入沙量的变化规律只对悬沙冲刷淤泥现象明显的河段有影响,因而来水来沙变化规律除特殊情况外对岸坡及河床的变形影响一般可忽略不计。另外,通过观察可以发现一般河道的泥沙组成每年是基本不变的,所以泥沙变化这一因素在研究岸坡及河床的冲刷淤泥时往往也忽略不计。由此可见水流的冲刷能力概括起来可以简化为两个影响引子,上游来水量 (Q)和上游输沙量 (S)。堤岸的抗冲能力主要与河岸土体性质、颗粒级配、粒间电化学作用、堤坡角度等因素有关,对于非黏性土河岸,当土体被水流冲动时,以单个颗粒的运动形式起动,抗冲力主要来自土体的有效重力,对于黏性土堤岸,当土体被水流冲动时,以大小不等的颗粒或泥块为起动单元,抗冲力主要来自土体的黏聚力[5]。堤岸的抗冲能力概括成对堤岸和河床的影响引子主要包括:河岸土体性质,河岸的比降(J),河床形态等因素。其中河岸土体性质对于一般河道常年是不会发生重大变化的,因而可以忽略不计。河岸的比降一般不易获取,但比降是由上下游水位确定的,上游水位的影响可以体现在上游来水量 (Q),可忽略,所以可以用下游水位 (Z)替代河岸的比降 (J)这一影响引子。河床形态一般由河岸的宽深比来体现 (B0.5/H),其中B为河宽,H为河深。因而堤岸的抗冲能力可以简化为两个影响引子,下游水位 (Z)和河床形态 (B0.5/H)。而对于河流冲刷作用下人工堤岸稳定性研究,我们所关注的是河岸的变形预测,所以预测模型的输出引子是平均淤积厚度 (△H)。综上所述,采用人工神经网络方法研究堤岸及河床的变形,输入引子简化为上游来水量 (Q)、上游输沙量 (S)、下游水位 (Z)和河床形态 (B0.5/H),输出引子为平均淤积厚度 (△H)。
1.2 人工神经网络模型各影响引子的获取
利用人工神经网络研究堤岸的演变和预测,输入引子和输出引子的获取是关键环节。实测资料丰富的情况下,一般都可顺利的定量确定各影响引子。对于堤岸及河床的变形预测模型中的影响引子,上游来水量 (Q)、上游输沙量 (S)和下游水位 (Z)一般可从上下游的各级水文站处获取,而河床形态 (B0.5/H)及平均淤积厚度可通过对地形图进行一定的图像处理来获得,此种获取途径有一定的误差,但一般可满足实际工程的需要。
1.3 人工神经网络模型的结构与工作原理
本文拟采用具有较强非线性映射能力的BP神经网络模型来研究堤岸及河道的变形。BP神经网络是神经网络中采用误差反传算法作为其学习算法的前馈网络,由输入层 (一层)、隐含层 (一层或多层)和输出层 (一层)组成,层与层之间的神经元采用全互连的连接方式,通过相应的网络权系数W相互联系,每层内的神经元之间没有连接(如图1所示)。BP神经网络的学习过程一般包括:“信息正向传播”→“误差反向传播”→“记忆训练”→“学习收敛”这4个部分组成[6]。BP网络在应用于预测预报之前,需要一个网络学习过程,然后才可以用建立好的模型进行预测,其工作原理也是非常清晰的,以BP神经网络预测堤岸及河道变形为例,将上游来水量 (Q)、上游输沙量(S)、下游水位 (Z)和河床形态 (B0.5/H)4个输入引子从输入层输入,经过隐含层逐层计算直到输出层得到的输出引子平均淤积厚度 (△H),比较输出引子平均淤积厚度 (△H)与期望值的差别,计算出误差,然后反向传播,通过网络将误差内容沿原路径传回各层神经元,并根据误差修改其权值,使得下次正向传播可以得到与期望值更为接近的信息。随着输入引子的正向传递与误差的反向传播的多次进行,通过BP神经网络得到的输出引子平均淤积厚度 (△H)逐渐趋近期望值,神经网络的学习过程也就随之结束。将要预测的输入引子上游来水量 (Q)、上游输沙量 (S)、下游水位 (Z)和河床形态 (B0.5/H)代入学习完成的BP神经网络模型,经过各层网络的传播,就可以得到我们期望的平均淤积厚度 (△H)预测值。
2 冲刷作用下堤岸稳定分析方法

图1 神经网络结构示意图Fig.1 Structure of neural network schematic diagram
冲刷作用下堤岸稳定分析方法是首先要确定堤岸的冲刷状态,然后根据边坡稳定方法计算堤岸被冲刷后的变形和稳定性,同时评价冲刷条件下堤岸的稳定性。此类方法在稳定分析方面基于极限平衡条件和土的摩尔-库仑准则,最早是根据侵蚀堤岸进行简单土坡稳定分析[7],或针对简单土坡的几何剖面与侵蚀堤岸几何剖面的差异,提出了考虑冲刷后几何剖面的堤岸稳定分析方法[8-10]。后来学者在此基础上又进一步改进,对破坏面位置、滑动面形状、静水压力和孔隙水压力作用等进行了考虑,针对不同的土质提出了不同的力学模拟方法和堤岸坍塌判别方法[11-16]。
在已有的研究成果中,基本局限于改进冲刷堤岸几何剖面和坍塌模式,而在稳定分析理论、冲刷条件下堤岸几何剖面改变后堤体内部变形特性及对稳定的影响、冲刷与渗流共同作用下堤岸稳定评价等方面研究较少。本文基于上述考虑提出了平面水动力学-土力学堤岸稳定耦合分析方法 (Levee Stability Coupling Model Based of Hydrodynamics Soil mechanics,LSCMHS),其具体过程为:
1)根据堤岸设计横断面确定自重应力和渗流力共同作用下的耦合应力场,根据堤岸土体特性选择适当的土体本构模型计算相应于上述耦合应力场的应变场 (变形场),作为冲刷条件下堤岸稳定分析的初始条件;
2)根据堤岸及河床变形的演变预测模型确定堤岸被冲刷后的几何形状,与设计剖面比较后确定冲刷后的计算横断面,再次通过计算确定耦合应力场和应变场,与冲刷前进行比较,根据塑性区域发展范围判别堤岸整体稳性和局部稳定特征;
3)采用强度折减法确定冲刷前后塑性区域特征,通过对塑性区和特征点位移值综合判定,给出整体安全系数和局部安全系数。
该方法需采用数值分析技术,并非商业软件中的计算方法,主要优点在于不必事先假设滑动面位置和形状,同时可以根据所选择的本构关系应用于不同的筑堤土体 (材料),在考虑冲刷作用的同时考虑自重应力和渗流力对堤岸稳定的影响,当计算不同工况时,还可以通过渗流场的计算考虑水位的上升与降落。
3 实例分析
3.1 基本概况
广东北江大堤某河段位于北江下游,水流冲刷作用已造成部分近岸河道下切,所形成的堤脚掏空对人工堤防的稳定构成明显威胁。(见图2)。
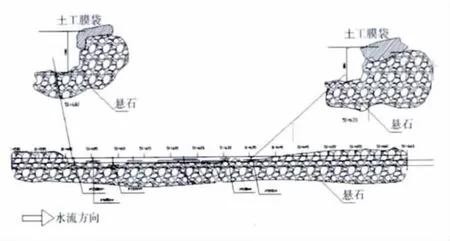
图2 典型断面堤脚被冲刷现象Fig.2 River scour phenomenon of the toe of slope in typical section
3.2 堤岸坡脚被冲刷预测
本文采用BP神经网络模型来对河段人工堤岸坡脚被冲刷情况进行计算与预测。根据水文资料确定计算断面的上游来水量 (Q)、上游输沙量(S)、下游水位 (Z)和河床形态 (B0.5/H)如表1,将其作为影响引子 (输入向量),平均冲淤厚度△H为冲刷结果 (输出向量),以1999年至2008年10个年份实测资料作为训练样本,2009年实测资料作为预测样本。

表1 计算河段各断面特征值统计表Table 1 Section eigenvalue statistical table
利用BP神经网络模型,根据研究断面的实测特征值进行网络学习和预测。由于各断面数据较多,每个断面选择高程为-2 m、-8 m、-12 m的岸线位置作为输出数据,计算结果和预测结果对比见表2。
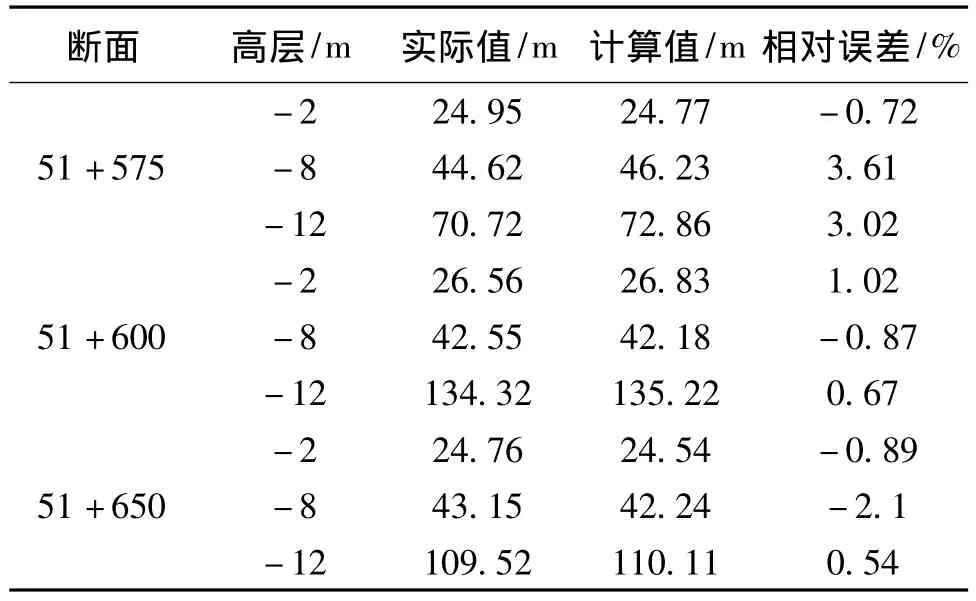
表2 各断面2009年坡脚岸线位置实际值与计算值对比表Table 2 Actual value and calculated value of the embankment toe shoreline in 2009
根据神经网络模型得到典型断面51+575的堤岸坡脚冲刷预测结果对比图 (见图3)。由图可见计算结果与实际情况基本一致,典型断面的坡脚岸线位置预测较为准确。综上可以看出,利用BP人工神经网络模型可以较准确的预测堤岸坡脚的冲刷变形情况,得到河流冲刷作用后的堤岸坡脚几何性状。

图3 典型断面河流冲刷预测结果对比图Fig.3 River scour prediction results contrast diagram of typical section
3.3 河流冲刷作用下堤岸稳定性分析
3.3.1 计算工况及计算方法 河流冲刷作用下人工堤坝稳定分析选择的典型断面如图3所示,根据堤岸的设计标准和实测资料绘出了初始设计断面(图4a)和由于冲刷作用形成的冲刷后断面 (图4b)。根据分析和堤坝的运行情况,计算时针对以下几种工况采用上述平面水动力学-土力学堤岸稳定耦合分析方法进行整体稳定分析:
1)高水位 (百年一遇)并形成稳定渗流;
2)枯水位并形成稳定渗流。

图4 冲刷前后的计算断面Fig.4 Computation sections before and after river scour
3.3.2 计算参数 根据岸坡土体特征,采用摩尔-库伦本构模型,根据现场取样和室内试验,确定堤基及堤身土质情况力学参数如表3所示。
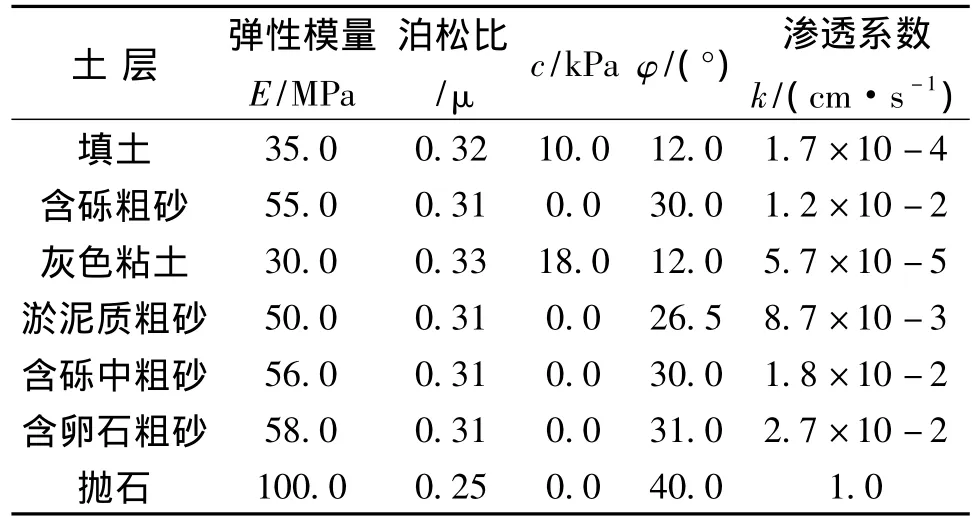
表3 计算选用参数Table 3 Calculation parameters
3.3.3 计算结果与分析 采用前述稳定分析方法对指定断面形式进行了不同工况下的整体稳定性分析,计算结果见表4,最危险滑弧位置见图5、图6,图中由浅色到深色区域代表等效塑性应变逐渐增大;设定冲刷前的岸坡状态为初始场,则由于河流冲刷作用造成坡脚坡面缺损后岸坡变形特征见图7,图中从浅到深色区域代表位移逐渐增大。

表4 堤坝边坡整体稳定安全系数计算结果汇总Table 4 Safety factor results of the overall stability of the slope

图5 高水位并形成稳定渗流时整体稳定分析Fig.5 Overall stability analyze with high water level and steady seepage flow
上述计算结果表明,高水位时堤坝冲刷前后整体稳定安全系数相差不大,表明堤坝在坡面或坡脚被冲刷后对其整体稳定影响不敏感;枯水位时坡面和坡脚被冲刷前后的整体稳定性有明显降低,局部区域出现了滑动破坏,从计算结果中看出在坡脚处塑性区贯通,出现小范围滑动,表明在水位较低时人工堤坝上游坡面对冲刷造成的坡脚处形状的变化比较敏感。采用平面水动力学-土力学堤岸稳定耦合分析方法,根据河床变形的演变预测模型确定了堤岸被冲刷后的几何形状,与设计剖面比较后确定了冲刷后的计算横断面,考虑了时间因素的影响。另外,冲刷作用形成的坡脚或坡面缺损可以导致坡面及坡脚产生附加变形,特别是被冲刷区域附近,这对于堤岸的安全运行来说是极为不利的。

4 结语
1)根据当前的实测资料预测未来冲刷结果对于人工堤防的运行是极为重要的,各种预测方法中人工神经网络因为简单易行,可考虑水动力因子的影响而具有实际应用的优势。本文所建立的模型可操作性强,实测资料验证了预测结果的可信。
2)通过对水流冲刷后的边坡进行的整体稳定分析和应力-应变分析表明了冲刷造成坡脚、坡面缺损后边坡整体稳定性的降低和冲刷区变形的增加。这种将基于人工神经网络的冲刷预测模型和边坡稳定分析模型相结合的水动力学-土力学堤岸稳定耦合分析方法可以将冲刷作用及对堤坝整体稳定的影响作为因果,极大的提升了河流冲刷模型的实际应用价值。此方法通过有限元模型极易拓展到各类非均质堤坝在冲刷条件下的变形分析和预警,具有较好的适宜性和实用性,这对于堤防建设和运行管理具有重要意义。
3)根据本文的研究思路,可结合可视化技术实现“实测-预测-稳定评价”的一体化自动分析,对于人工堤防的运行管理具有实际应用价值,可以实现冲刷条件下堤坝边坡的预测预警。
[1]张小峰,徐全喜,谈广鸣,等.河道岸线变形神经网络预测模型研究[J].泥沙研究,2001,10(5):19-26.
[2]陈一梅,徐造林.基于神经网络的河道浅滩演变预测模型[J].水利学报,2002,8(8):68-72.
[3]虞娟,陈一梅.河道岸线演变预测方法研究[J].三峡大学学报,2005,27(4):305-308.
[4]DARBY S E,THOME C R.Closure of Discussion of Development and testing of riverbank-stability analysis[J].Journal of Hydraulic Engineering,1997(11):1052 -1053.
[5]王昌杰.河流动力学[M].北京:人民交通出版社,2001:10-45.
[6]胡铁松.神经网络预测与优化[M].大连:大连海事大学出版社,1997:23-78.
[7]THOME C R.“Processes and mechanisms of river bank erosion”Gravel-bed rivers[M].England:John Wiley and Sons Inc,1982:227-259.
[8]OSMAN A M,THOME C R.Riverbank stability analysis I:Theory[J].Journal of Hydraulic Engineering,1988,114(2):134-150.
[9]THOME C R,OAMAN A M.Riverbank stability analysisⅡ:Application[J].Journal of Hydraulic Engineering,1988,114(2):151-172.
[10]DARBY S E,THOME C R.Development and testing of riverbank-stability analysis[J].Journal of Hydraulic Engineering,1996,122(8):443-454.
[11]傅旭东,邹勇,邹中勇.兴山县龙王嘴边坡稳定性分析与加固设计[J].岩土力学,2003,24(S2):271-274.
[12]刘华强,殷宗泽.膨胀土边坡稳定分析方法研究[J].岩土力学,2010,31(5):1545-1549.
[13]傅旭东,茜平一,刘祖德.边坡稳定可靠性的随机有限元分析[J].岩土力学,2001,22(4):413-418.
[14]王洋,汤连生,杜赢中.地下水渗流对基坑支护结构上水土压力的影响分析[J].中山大学学报:自然科学版,2003,42(2):107-110.
[15]邓东平,李亮.水力条件下具有张裂缝临河边坡稳定性分析[J].岩石力学与工程学报学,2011,30(9):1835-1847.
[16]王洋,汤连生,高全,等.水土作用模式对残积红粘土力学性质的影响分析[J].中山大学学报:自然科学版,2007,46(1):128-132.

