面向作业车间重调度的改进合同网机制研究*

丁彬楚，汤洪涛

（浙江工业大学 工业工程研究所，浙江 杭州 310014）

0 引 言

车间初始生产调度方案实际执行时，会遇到各种各样的扰动，这些扰动会带来重调度的需求，并且这些扰动对重调度方法的实时性、动态性及其耦合能力都有很高要求。基于多Agent的调度技术采用协商机制解决调度决策中的各类冲突，能够准确地反映系统的动态重调度过程，降低问题求解的复杂性，对动态的现实环境具有良好的灵活性和适应性。

现有的协商机制中基于合同网（CNP）的协商机制最为常用，一般认为，合同网协商机制具有较好的开放性以及动态分配和自然平衡能力。但是，传统的合同网协商机制仅仅规定单一的工作过程，本身没有优化能力和动态学习能力，因此具有自学习能力的合同网协商机制成为了该领域研究的热点。Csaji等[1]以提高Agent的学习能力为目的，提出了基于时间差分学习算法TD(λ)，从而在协商过程中获得更好的投标者。Wang和Usher[2-3]为解决动态单机调度问题中调度规则动态优化选择的问题，集成了强化学习中的Q-学习和CNP机制。王世进等[4]在此基础上，深入探讨了集成Q-学习和CNP机制的分布式柔性作业车间环境下作业动态分配优化问题，给出了具有针对性的集成机制的策略决策过程和学习过程。Q学习能够使Agent从给定的调度规则中选择出较好的调度规则，但是当这些启发式规则在学习中得不到最优解时，不能及时得到修正，并且Q学习本身无规划能力，不能满足重调度需求。张化祥等[5]通过考虑个体多步进化效果优化变异策略的选择，提出了一种基于Q学习的适应性进化规划算法（QEP），用变异策略代替了启发式规则，提供了更多的交互机会，使Q学习更具有广泛性。

在以上Q学习、QEP等算法的研究基础上，本研究将其应用于动态重调度问题的研究，并引入滚动窗口技术改进QEP算法，提出集成QEP和CNP的协商机制，以实现柔性作业车间动态重调度过程。

1 重调度假设及目标

本研究中的动态重调度针对的对象为柔性作业车间，给出假设条件如下：

（1）各设备同一时刻只能加工一个工件；

（2）工件在设备上的加工时间已知；

（3）正在加工的工件不进行重调度；

（4）调度过程中除设备以外的其他资源充足，无需调度。

重调度的目标描述如下：首先，仍应尽量保证原调度方案的优化目标，即最大完成时间最小；其次，在实际的生产过程中，调度系统总体上是按照初始调度方案准备调度所需加工工具和材料，当调度方案改变时，势必会造成这些工具和材料的运输和浪费，所以重调度产生的调度方案应尽量减少与当前调度方案的差异，即最小化与重调度前调度方案的背离。

对于多目标的求解方式主要有3种：决策先于优化、决策与优化交替以及优化先于决策[6-7]。本研究采用传统的决策先于优化的方式，给出重调度目标函数数学表达式如下：

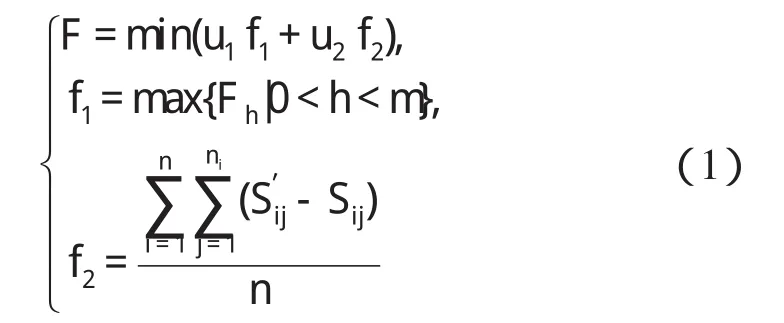
式中：m—作业车间设备数量，n—调度工件数，ni—工件i的工序数，Fh—设备h完成所有任务的时间，Sij—工件i第j道工序重调度前的开工时间，S′ij—重调度后开工时间。

2 改进QEP重调度算法

本研究给出的调度目标重点在于吸收和修复动态事件对调度的影响，因此笔者引入滚动窗口重调度技术。滚动窗口技术的应用可以减少动态重调度涉及的对象，缩小问题求解的规模[8]，并将该技术集成到QEP算法中，使算法在求解重调度问题时具有合理的规划性，避免盲目进化，提高进化效率。

改进QEP算法流程设计如图1所示。

图1 改进QEP算法流程

2.1 滚动窗口初始化及更新设计

当生产过程中有扰动事件发生时，某工件当前加工工序受到影响,并且由于该工件受到工序约束和设备约束，影响会进一步扩散，即重调度的扩散效应[9]。研究者通常采用二维分支树（即工件分支和设备分支）来描述该扩散过程。滚动窗口初始化和更新建立在这种扩散过程的基础上。

针对3种常见扰动事件，滚动窗口初始化方法为：

（1）加工延迟。初始滚动窗口为延迟工件两分支上的工单；

（2）设备故障。初始滚动窗口为故障设备故障时间内待加工工单，如果设备故障时间未知，则表示为故障设备上所有工单；

（3）故障恢复。初始滚动窗口为所有可在该设备上加工的工单，已完工和正在加工的工单除外，同时滚动窗口内工单按照开工时间的先后顺序进行排列。

本研究设计了局部和全局两种滚动窗口更新方法。局部更新是针对某一工单进行更新、整合，步骤如下：

（1）以更新的工单为根节点，将工件分支和设备分支上的工单加入滚动窗口并删除更新的工单；

（2）去除滚动窗口中重复的、无延迟发生的工单；

（3）按照工单开工时间的先后顺序进行排序。

全局更新是针对滚动窗口内所有工单进行更新、整合，步骤如下：

（1）根据当前滚动窗口，将各工单工件分支和设备分支上的工单作为当前滚动窗口，替换原滚动窗口，在二维分支树上表示为下一层的工单集；

步骤（2）、（3）同局部更新。

2.2 进化分析

Q学习通过选择最大化Agent带折扣累积收益的行动，可以学习到Agent的最优行动集。进化过程中，研究者若把个体变异策略看成行动，则个体选择最优变异策略就转化为Agent选择最优行动，在选择最优行动时考虑行动的立即及多步滞后收益，即计算折扣累计收益。

本研究假设个体进化步长为m(m>1)，即考虑m-1步滞后收益，个体开始选择变异策略为a，可以计算个体采用行动a时的收益为：

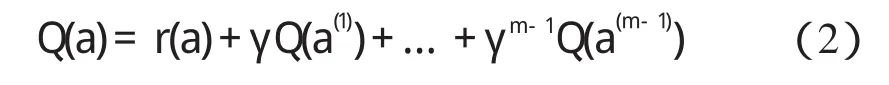
式中：r(a)—个体采用变异策略a的立即收益，此时个体进化了一次。

新生成的个体采用a(1)生成新个体，此时收益记为Q(a(1))，依次类推，m-1次进化后，新生成的个体采用a(m-1)生成新个体，此时收益记为Q(a(m-1))。式（2）为个体采用a，a(1)，…，a(m-1)变异策略集的累计收益。定义个体立即收益r(a)=fp(a)-fo(a)。其中：fp(a)—父代个体对应的适应度值，fo(a)—采用变异策略a后生成的子代个体对应的适应度值。适应度函数计算公式如下：

其中，函数f1，f2已在公式（1）中给出。本研究将立即收益代入式（3），得到Q值的计算公式为：

2.3 改进Q学习过程设计

在Q学习过程中，为保证滞后收益对Q(a)的有效性，本研究针对每个个体分配了一个临时滚动窗口。

个体Q学习流程设计如图2所示。

Step1：获取临时滚动窗口，设置进化代数t=2；如果临时滚动窗口为空，转入step5；

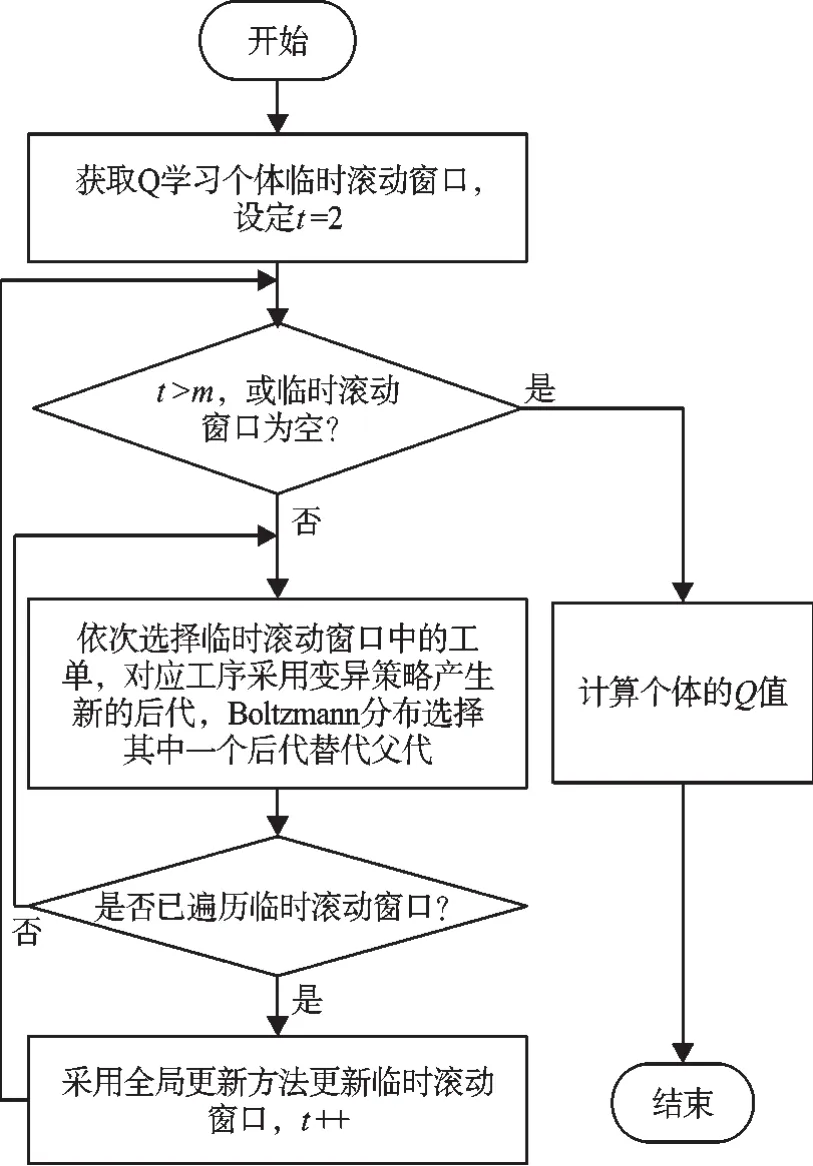
图2 Q学习流程图

Step2：遍历临时滚动窗口中每一个工单，采用Boltzmann选择每一个工单对应工序的变异策略；Boltzmann分布计算变异策略被保留下来的概率为：

式中：n—工序变异产生的后代个数；α—调节系数，α∈(0,1)；T0—初始温度。

在Q学习的初始阶段，温度参数T设置较高，系统探索未尝试的动作（选择非最优变异策略），以获得更多回报的机会；在Q学习的后期，笔者设置较低的温度参数，使系统倾向于利用当前最优的变异策略。

Step3：采用全局更新的方法更新临时滚动窗口，同时设置进化代数加1；

Step4：判断t是否大于m，或者临时滚动窗口为空；满足条件则转step5；不满足则转step2；

Step5：计算个体的Q值，Q学习结束。

以下给出m=2时的Q学习过程示意图：

图3 Q学习过程示意图

2.4 变异策略

基于文献[10]的研究，本研究给出以下变异策略：

（1）工序所用设备不变，加工顺序不变，只是调整各个工序的开始时间和结束时间，记为“设备不变，顺序不变”；

（2）工序所用设备不变，但在设备内的加工顺序可以调整，记为“设备不变，顺序可变”；

（3）工序使用设备发生变化，插入到并行设备加工列表中，记为“设备可变，顺序可变”。

3 集成QEP的改进合同网协商机制

扰动事件发生时，集成QEP的合同网机制协商过程如图4所示。其基本交互过程发生在工序Agent（PA）和设备Agent（MA）之间。

图4 QEP-CNP协商流程图

基本流程描述如下：

Step1：初始化滚动窗口；

Step2：获取滚动窗口中的第一个工单，生成相应的工序Agent（PA），解除原先合约，并获取调度需要的相关信息，包括加工时间、可加工设备、设备上的工单列表等；

Step3：PA向能够加工它的设备发送招标请求；

Step4：设备Agent（MA）作为投标方进行Q学习，根据工件平均背离、总完成时间和设备负载等生成多份标书，向PA发送应标信息；

Step5：PA评价各MA发回的投标书，选择中标的MA和最优变异（最大Q值），更新调度方案；两份标书评价值相等时，根据设备负载，选择负载小的MA和最优变异策略；

Step6：采用局部更新方法更新滚动窗口；

Step7：判断滚动窗口是否为空；否，转Step2；是，协商结束，输出调度方案。

4 仿真实验

本研究将文献[11]给出的10×10标准算例调度最优解作为初始调度解，其甘特图如图5所示。笔者针对表1给出的动态事件进行重调度仿真。

图5 10×10甘特图（最短加工时间：t=7 s）

表1 动态事件表

动态重调度算法选择参数如下：完成时间权重为0.8，工时偏差权重为0.2，进化步长为2，变温调节系数为0.8，初始温度为10。由于重调度协商过程中工件和设备目标明确，容易达成一致，直接受影响的工件重调度所需要的时间可以忽略。

本研究通过仿真得到3个时刻重调度后的甘特图如图6所示。

本研究将改进的合同网协商机制与基本合同网协商机制相比，得到的仿真结果如表2所示。通过对比可以看出，改进的合同网协商机制具有较好的全局优化性能。

表2 仿真结果表

5 结束语

图6 动态重调度甘特图

本研究针对面向作业车间重调度问题的改进合同网协商机制进行了研究，设计了改进的QEP算法，提出了集成QEP和合同网的协商机制。该协商机制具有良好的反应能力和全局优化性能，但同时也存在如下问题：

首先，针对多目标问题，研究者在设计目标函数时采用简单的加权法虽然提高了系统的反应能力，但是在一定程度上削弱了系统的优化能力；

其次，通过集成改进的QEP算法和合同网，虽然使得多Agent具有一定的自学习能力，但出于系统时间性能的考虑，简化了Q学习每一步的进化操作，并且算法中的变异策略冗余度较高，未能做出有效优化。后续研究将从这几方面进一步改善合同网机制。

（References）：

[1] CSAJI B，MONOSTORI L，KADAR B.Reinforcement learn⁃ing in a distributed market-based production control system[J].Advanced Engineering Informatics，2006，20（3）：279-288.

[2] WANG Y，USHER J.Application of reinforcement learning for agent-based production scheduling[J].Engineering Applications of Artificial Intelligence，2005，18（1）：73-82.

[3] WANG Y，USHER J.A reinforcement learning approach for development routing policies in multi-agent production scheduling[J].The International Journal of Advanced Manufacturing Technology，2007，33（3/4）：323-333.

[4] 王世进.面向制造任务动态分配的改进合同网机制[J].计算机集成制造系统，2011（6）：1257-1263.

[5] 张化祥，陆 晶.基于Q学习的适应性进化规划算法[J].自动化学报，2008（7）：819-822.

[6] 陈 宇.不确定环境下的多Agent鲁棒性生产调度研究[D].广州：广东工业大学自动化学院，2009.

[7] 崔逊学.多目标进化及其应用[M].北京：国防工业出版社，2006.

[8] 邵斌彬.柔性制造动态多目标调度模型在MES中的研究与应用[D].上海：上海交通大学软件学院，2008.

[9] MARLER R，ARORA J.survey of multi-objective optimiza⁃tion methods for engineering[J].Structural and Multidis⁃ciplinary Optimization，2004，26（6）：369-395.

[10] 丁 雷，王爱民，宁汝新.工时不确定条件下的车间作业调度技术[J].计算机集成制造系统，2010（1）：98-108.

[11] 李修琳，鲁建厦，柴国钟，等.混合蜂群算法求解柔性作业车间调度问题[J].计算机集成制造系统，2011（7）：1495-1500.