希尔伯特-黄变换在电压闪变测量中的应用
赵英男,陈隆道*,文昊翔,张 帆
(1.浙江大学 电气工程学院,浙江 杭州 310027; 2.吉林省电力勘测设计院,吉林 长春 130022)
0 引 言
随着现代电力系统的飞速发展,电能质量已成为衡量电力系统运行水平的一个重要内容,因此对电能质量的准确测量及监控就显得格外重要。
电压波动和电压闪变是衡量电能质量的重要指标。电压波动是电压均方根值一系列相对快速变动或连续改变的现象。电光源的电压波动造成灯光照度不稳定的人眼视感反应称为电压闪变[1]。由此而知,闪变是电压波动引起的视觉效果。国际电工组织(International Electrotechnical Commission,IEC)提出用瞬时视感度S(t)来量化人的瞬时主观感受,该值是通过对电压波动值进行计算而得到的,研究者通过对该值的统计计算得到电压闪变的评价指标:即短时闪变严重度Pst与长时闪变严重度Plt。
现今对电压闪变的测量,比较常用的是基于IEC推荐的方法而研制的数字化闪变仪,对该种仪器的改善主要集中在误差校正以及实践方式上[2-3]。另外一种应用较多的是在IEC 测量原理的基础上进行简化与改进,用FFT 分析。文献[4]使用了加窗插值的FFT 算法,并对S(t)繁琐的推导运算进行了简化。但以上两种方法都不能给出各参量随时间的变化情况,输出的S(t)值由于算法限制数量有限。
HHT 算法是NE.Huang 等人[5]提出来的一种自适应信号处理方法。HHT 适用于非线性、非平稳信号处理,具有多分辨率的特点,已广泛应用于地震信号、语音信号以及电力信号处理等领域[6-8]。研究者用HHT代替FFT 测量电压闪变值,对带有闪变成分的电压信号进行时频分析,可以获得电压信号与瞬时闪变视感度在各时间点上的具体参数,通过统计计算得到短时闪变严重度。
本研究主要探讨HHT 在电压闪变测量中的应用。
1 希尔伯特—黄变换
希尔伯特—黄变换(HHT)首先将复杂的多成分信号用经验模态分解(Empirical Mode Decomposition,EMD)的方法分解成一系列单成分的信号,称为本征模态函数(Intrinsic Mode Function,IMF)。任何信号都可以分解为满足一定条件的有限个IMF 之和[9]。
对信号进行EMD 分解是一个不断提取高频分量的过程。本研究对信号X(t) 进行分解,第 j 个IMF 分量为C(jt)。r(Nt)为残余分量,代表信号的趋势,即:
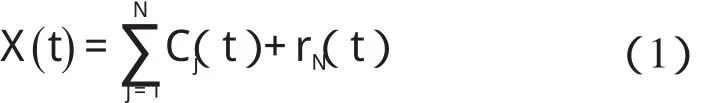
式中:N—分解的IMF 个数。
研究者在提取IMF 分量时要注意每个分量提取结束的终止条件的选择,如果终止过迟、筛选过度,就会造成所得到的固有模态振荡趋于等幅振荡,无法反映出原始信号的物理特性。但如果终止过早就只能得到粗糙的IMF 分量,影响到计算的精度[10]。在对电压波动信号进行分析时,终止条件的选择至关重要,关系到Hilbert 变换与闪变值计算的准确度。
由于一个本征模态函数中只包括一种形式的振荡,对各IMF 分量进行希尔伯特变换后所得到的瞬时频率没有负频率,有实际的物理意义。
HHT 方法的第2 步是对各IMF 分量进行Hilbert 变换:

解析信号为:

瞬时幅值为:

瞬时相位为:

瞬时频率为:
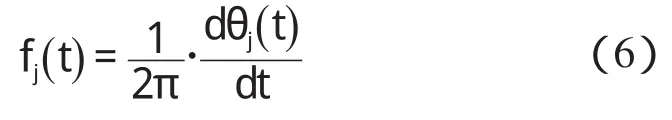
2 HHT 测量电压闪变的基本原理
2.1 闪变测量步骤
设电压波动信号为工频载波的调幅波,且满足下式:
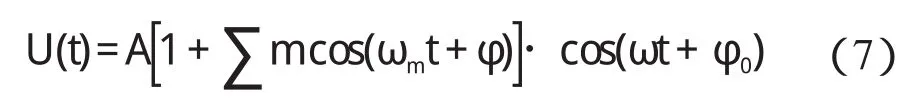
式中:A—工频电压幅值,ωm—调幅波角频率,φ—调幅波初相位,ω—工频电压角频率,φ0—工频载波初相位。
设采样频率为4 kHz,采样后电压序列U(n),根据电压波动的定义,求得半个工频周波(0.01 s)内电压均方根值序列为:
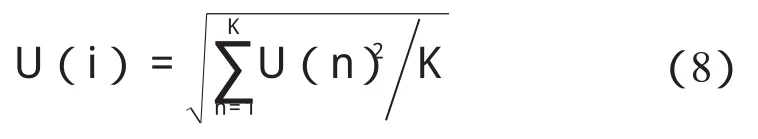
式中:K—每半个工频周波的采样点数,值为40。
本研究采用Hilbert 法提取包络[11]得到波动量Uf(t),人眼对闪变的敏感频率范围是0.02 Hz~35 Hz,信号通过0.02 Hz~35 Hz 滤波器后,进行EMD 分解,将信号表示成N 个IMF 分量的和,即:
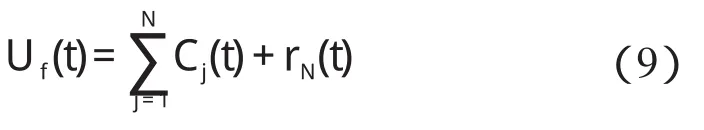
式中:Cj(t)—第 j 个IMF 分量,rN(t)—残余分量。
本研究对各IMF 分量进行Hilbert 变换,如式(2~6)所示。原信号是解析信号的实部,得到各分量的瞬时幅值Aj(t)、瞬时相位θj(t) 以及瞬时频率 fj(t)。由于分析对象是电压的半波有效值,实际时间应该乘以0.01 s。
根据电压波动定义,电压波动等于调幅波的峰-峰值对工频额定电压有效值的百分值:
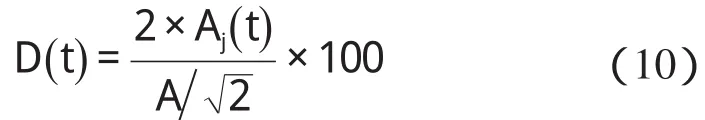
根据瞬时视感度与电压波动的平方成反比[12],本研究用实际电压波动值除以对应频率正弦波产生一个闪变单位所对应的电压波动值,即得到该频率对应的瞬时视感度Sj(t):

IEC给出了产生觉察单位闪变的电压波动-频率曲线,而在未给出的频率点,运用3次样条插值的方法求出。由于电压信号的瞬时幅值与瞬时频率是时刻变化的,插值过程也是在时刻进行的。
多个分量的瞬时视感度为各个分量所产生的所有瞬时视感度的总和:

最后对瞬时闪变视感度进行统计分析,用下式可得到短时闪变严重度:

式中:P0.1,P1,P3,P10,P50—10min内统计的 S(t)的概率大值[13]。
测量框图如图1所示。
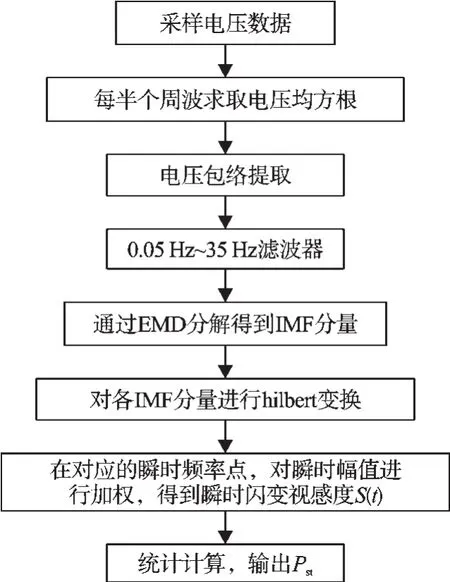
图1 闪变测量框图
2.2 计算实例
由于对每半个工频周期的电压信号求一次均方根值无法得到精确的正弦波形,在后面的计算难以分析结果的准确性,本研究直接假设求得均方根后的电压波动信号为:
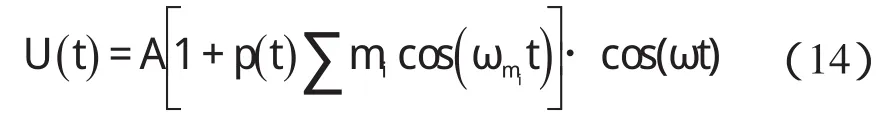
截取20s内的信号,有2000个均方根值。
设发生闪变的时间为5s~15s之间。则有:

本研究在提取包络后对波动信号进行EMD分解,调用Matlab中EMD函数时将终止条件设置成:OPTI⁃IONS.STOP=[0.0001,0.2,0.0001]。该信号含有两个频率分量,分别为10Hz和20Hz,由于均为等幅正弦振荡,分解出来的IMF分量应该分别为20Hz与10Hz的正弦波。
本研究对每个IMF分量进行Hilbert变换,分别得到两个IMF分量的瞬时幅值与瞬时频率,仿真结果如图2、图3所示。
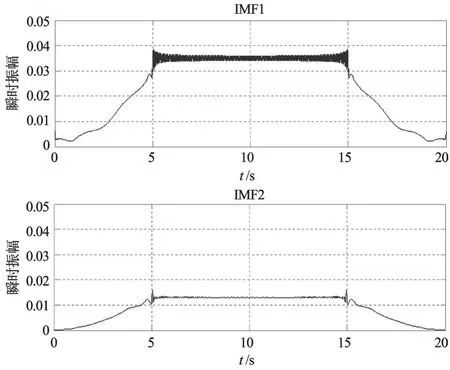
图2 各IMF分量的瞬时幅值
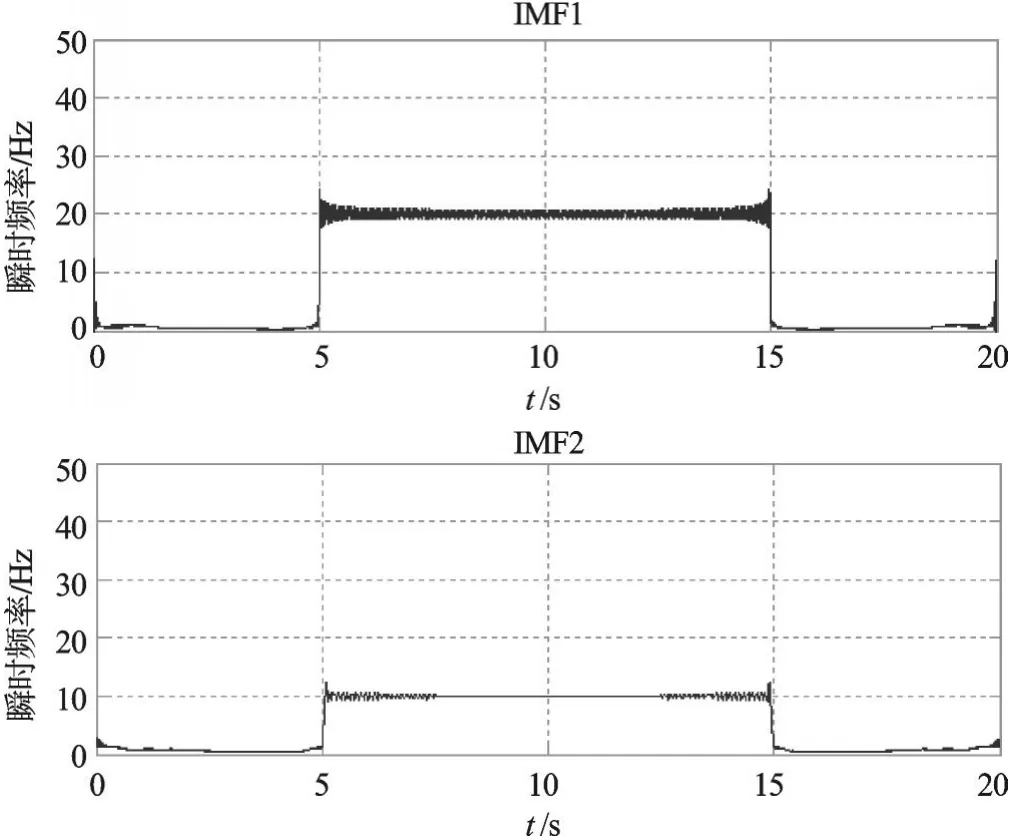
图3 各IMF分量的瞬时频率
笔者对瞬时幅值在相应频率处加权,得到瞬时视感度,如图4所示。
由仿真结果可以看出,HHT法反映了闪变发生的时间,并能够准确得到瞬时闪变视感度的大小。如果闪变连续发生,测量10min后可以得到60000个S(t)值,用概率大值法可得到统计结果为0.97074,理论计算结果为,误差为3.863%,达到了IEC 误差在5%内的要求[14]。

图4 瞬时闪变视感度
3 HHT 与IEC 以及FFT 的比较
关于S(t)的获得,相对于IEC 和FFT 的测量方法,运用HHT 的分析方法有着明显的优势。
由于IEC 测量方法的实现以滤波器为基础,研究者对一段数据进行处理时数据的前一段很不稳定,只能取后半部分甚至最后20 个数据进行计算,有时会漏掉重要信息。且最后一步平滑加权滤波器并非理想的滤波器,对于低频信号(如0.5 Hz,1 Hz)并不能完全滤除,这时S(t)波动较大,要取平均值来较小误差。这样每次计算输出的S(t)是经过了取舍与平均的结果。
本研究运用FFT 分析时,为了得到一定的频谱分辨率,需要增加数据长度。当采样频率为 fs=400 Hz时,分辨率要达到0.1 Hz,N 要取到4 096,即4 096 个数据后(81.92 s),可以输出一个P 值,该值为用FFT计算的S(t)等效值,即使采用滑块采样重复处理数据,10 min 内能够输出的P 值也非常有限,使得统计计算的精度并不高。
而运用HHT 分析时,由于S(t)是对瞬时电压幅值A(t)处理的结果,S(t)也具有实时性,即每0.01 s 就能得到一个S(t)值,能够准确显示闪变的大小与发生时间,并为短时闪变严重度Pst以及长时视感度P lt 的统计提供了充足的数据,提高了统计的准确度。笔者将计算实例数据进行重复测量,分别用3 种方法得到的S(t)值如图5 所示。
另外,由于EMD 分解是依赖信号本身的自适应过程,HHT 的方法是具有多分辨率特性的。每个IMF 分量的分辨率各不相同,含有高频成分的分量频率分辨率低,含有低频成分的频率分辨率高。第i 个IMF 分量的频率分辨率可由下式计算[15]:


图5 IEC,FFT 及HHT 法的S(t)值比较
式中:fimax—第i 个IMF 分量含有的最高频率,N—数据长度。
由于人眼对电压闪变的敏感范围是0.02 Hz~35 Hz之间,信号经过滤波后含有的最高频率为35 Hz。研究者若对2 000 点数据进行计算,当信号的最高频率为35 Hz 时,其频率分辨率可以达到0.001 75。而若用FFT 法计算,其频率分辨率与采样频率及数据长度有关,采样频率为400 Hz,数据长度需要达到为4 096个,才能达到分辨率小于0.1 的要求。因此HHT 算法在频率分辨率上远远优于传统的FFT 算法。
4 结束语
本研究根据所提出的电压闪变测量方法,通过对电压波动信号进行HHT 变换,可以得到电压波动信号的时变信息以及及时有效的瞬时闪变视感度值。与IEC、FFT 相比,基于HHT 的测量方法能够输出更完整详细的数据,便于精确找到闪变发生与结束的时间,为电能质量提供分析依据。
该方法频率分辨率高,可以应用于非平稳电压信号的闪变测量中。相对于IEC、FFT 方法,其应用范围更加广泛。
(References):
[1]肖湘宁.电能质量分析与控制[M].北京:中国电力出版社,2010.
[2]贾秀芳,赵成勇,胥国毅,等.IEC 闪变仪误差分析及改进[J].电工技术学报,2006,21(11):121-126.
[3]冯 亮,张有兵,翁国庆,等.基于TMS320C6713 DSP 的IEC 电压闪变仪[J].机电工程,2011,28(9):1144-1148.
[4]滕召胜,罗志坤,高云鹏,等.基于虚拟仪器的平方检测法电压闪变测量实现[J].仪器仪表学报,2011,32(8):1803-1809.
[5]HUANG N E,SHEN Zheng,LONG SR,etal.The empiri⁃cal mode decomposition and the Hilbert spectrum for non⁃linear and non-stationary time series analysis[C].Proc.R.Soc.Lond,1998:903-995.
[6]张义平,李夕兵,赵国彦.基于HHT 方法的爆破地震信号分析[J].工程爆破,2005,11(1):1-7.
[7]宋倩倩,于凤芹.基于Hilbert-Huang 变换和听觉掩蔽的语音增强法[J].声学技术,2009,28(3):280-283.
[8]李天云,赵 妍,韩永强,等.Hilbert-Huang 变换方法在谐波和电压闪变检测中的应用[J].电网技术,2005,29(2):39-43.
[9]伍青安,袁 越,吴博文,等.基于Hilbert-Huang 变换的风电场闪变[J].电网与清洁能源,2011,27(4):73-77.
[10]段生全.高精度时频分析及应用[D].成都:成都理工大学信息工程学院,2005:15-50.
[11]MAREIM I,TAREK K.Abdel-Galil,Ehab F.EI-Saadany,etal.Hilbert Transform based control Algorithm of the DG Interface for voltage flicker mitigation[J].IEEE Transac⁃tions on Power Delivery,2005,20(2):1129-1133.
[12]粟时平,刘桂英.现代电能质量检测技术[M].北京:中国电力出版社,2008.
[13]周 文,毛志芳,毛志强.电压闪变算法的MATLAB 仿真及DSP 实现[C].中国国际供电会议,2008.
[14]国家标准化管理委员会.GB/T 12326-2008 电能质量电压波动与闪变[S].北京:中国标准出版社,2009.
[15]盖 强,张海勇,徐晓刚.Hilbert-Huang 变换的自适应频率多分辨率分析研究[J].电子学报,2005,33(3):563-566.

