基于STM32的高精度电子天平
樊 毅,秦会斌
(杭州电子科技大学 电子信息学院,浙江 杭州 310018)
0 引 言
电子天平是高精度质量计量仪器,广泛应用于科研机构、高等院校和实验室,具有称量准确度高、响应速度快、稳定性好等特点[1]。目前,国内生产的电子天平,电路集成度低,研究者多采用分离的A/D转换器加放大器的电路,且采用模拟电路实现非线性修正和温度补偿,存在电路复杂、准确度低、可靠性差等问题[2]。国外生产的一些电子天平能够达到很高的准确度和可靠性,但是它们使用的称重传感器的成本都非常高,这样就使得整机的成本过高。
针对这些问题,本研究设计一种高精度、低成本的电子天平。该设计采用HX 711芯片对传感器的输出信号进行放大和模数转换,采用滑动均值滤波法进行滤波[3]。
1 电子天平工作原理
该设计选用了成本较低而且使用广泛的电阻应变式称重传感器来进行物理量的变换,把重量变换成电信号[4]。
HX711为称重传感器提供一个激励电压,有重物加载到称重传感器上时,它输出一个比较小的电压信号;HX711在接收到这个电压信号后,对其进行放大,然后进行A/D转换,直接变换成数字信号送给STM32进行处理;STM32对HX711送过来的数字信号先进行数字滤波,然后进行曲线拟合、标定等等一系列的处理,并转换为代表重物质量的数字量,送给12864液晶进行显示。
另外,在重物超过称重传感器的量程时,超载报警电路会发出报警的声音和光信号,以便让用户快速进行处理,避免损坏称重传感器;矩阵键盘输送相应的按键信号给STM32,以便实现去皮和单位转换等功能。
2 硬件设计
该设计主要由主控制器STM32、称重传感器、A/D转换模块HX711、超载报警电路、矩阵键盘、液晶显示模块12864这几部分组成[5]。
天平主要部分的电路图如图1所示。
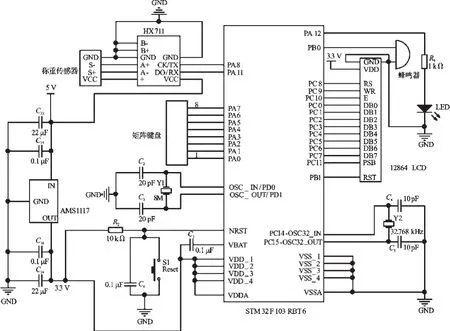
图1 电子天平主要部分电路图
该设计使用的电阻应变式称重传感器的具体参数如表1所示。
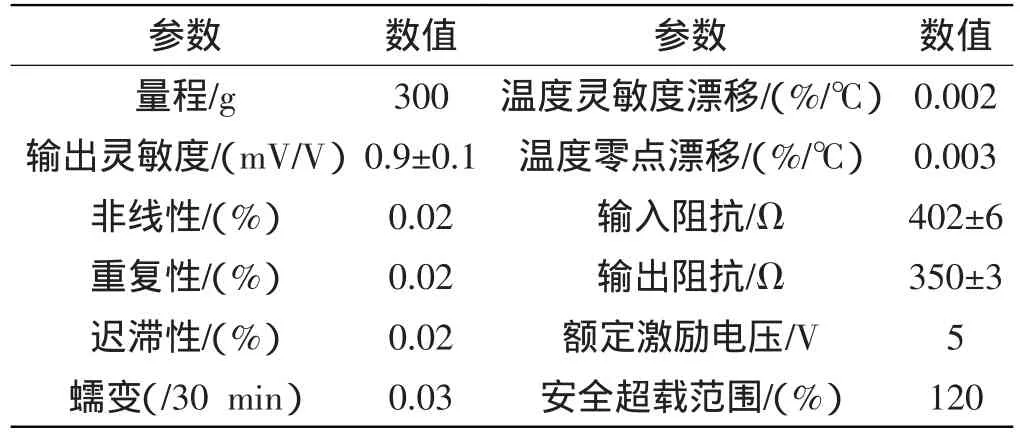
表1 电阻应变式传感器的各项参数
3 程序设计及技术特点
电子天平程序流程图如图2所示。
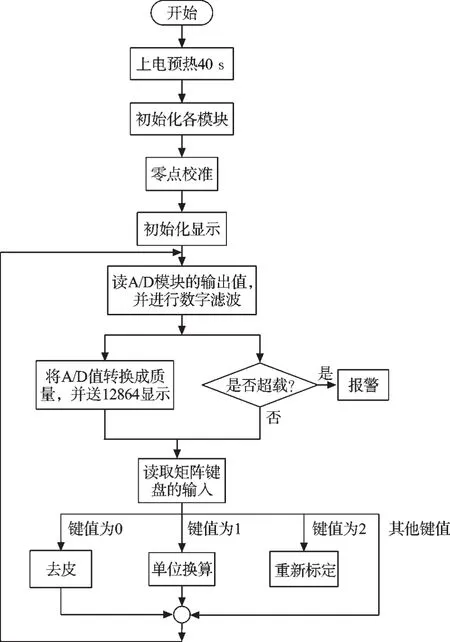
图2 电子天平程序流程图
为了达到较快的称量速度和较高的精度,该电子天平采用了几个具有创新性的设计。实验结果证明,这些设计使整个系统达到了预期的要求。
3.1 24位A/D转换器芯片HX711
目前市面上的电子天平多采用分离的A/D转换器和放大器组成的电路,对传感器输出的模拟信号进行处理。这样,不但增加了电路的复杂度,使电路稳定性降低,并且容易受到外界的干扰[6]。对于高精度电子天平来说,这种电路的复杂度造成的不稳定性会更加明显[7]。
为了避免以上问题,本研究采用了海芯科技集团生产的HX711芯片。该芯片是一款专为高精度电子天平而设计的24位Delta-Sigma型A/D转换器芯片。与同类型其他芯片相比,该芯片集成了放大器、稳压电源和片内时钟振荡器等其它同类型芯片所需要的外围电路,具有响应速度快、抗干扰性强等优点,降低了电子天平的整机成本和电路的复杂度,提高了整机的可靠性。
该芯片内提供的稳压电源可以直接向外部传感器和芯片内的A/D转换器提供电源。如果使用该芯片内提供的稳压电源给外部传感器供电,就不需为A/D转换器提供参考电压,这样就采用了电压比例测量法进行测量,整机的稳定性进一步提高,使整个电子天平能够达到较高的精度。并且,为了防止电源电压的波动造成过高的输入电压,而烧坏HX711芯片,本研究在电路中安装了一个5.1 V的稳压管。
3.2 高时钟频率低功耗的单片机STM32
目前的电子天平多采用51单片机这类功能较简单、时钟频率较低的单片机[8],这样,就存在称量速度慢、不易扩展复杂功能的弊端,为此,该设计采用目前市面上使用广泛的以ARM Cortex-M3为内核的STM32单片机作主控制器。
该设计采用的STM32F103“增强型”系列单片机,时钟频率达到72 MHz,是同类产品中性能最高的产品。其功耗为36 mA,是32位市场上功耗最低的产品,相当于0.5 mA/MHz。其工作温度范围为-40℃~+85℃,在温度变化较大时,仍能保持稳定的性能,使得该设计对温度变化的适应性增强。
实测结果表明,该设计称量速度快,充分预热后,10 s左右即可达到稳定读数。
3.3 滑动均值滤波法
为了降低电路复杂度,降低功耗,提高电路稳定性,本研究没有采用硬件滤波的方法,而是采用将A/D转换器输出的模拟信号直接数字化,再进行数字滤波的方法,降低了电路复杂度,提高了设计的稳定性。另外,该设计采用了滑动均值滤波法来进行滤波[9]。
滑动均值滤波法,属于数字滤波器中的有限脉冲响应滤波器。其原理是:把N个测量数据看成一个队列,队列的长度固定为N,每进行一次新的采样,把采样结果放入队尾,而去掉原来队首的一个数据,这样在队列中始终有N个“最新”的数据,对比普通的均值滤波法(每次都必须读入N个数据的方法),速度提高了很多。滑动均值滤波法的优点是,对周期性干扰有良好的抑制作用,平滑度高,适用于高频振荡的系统;缺点是,灵敏度较低。但是,对电子天平来说,它的灵敏度已经足够了。另外,该滤波法对偶然出现的脉冲性干扰的抑制作用差[10],本研究改进了滑动均值滤波法,增加了去除N个数据中的最大值和最小值的算法,提高了对脉冲性干扰的拟制作用,克服了滑动均值滤波法本身的弱点。改进后的滤波公式为:
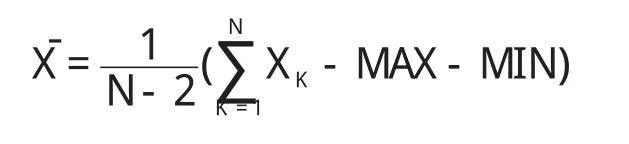
式中:—滤波后的结果,XΚ—第K次的A/D转换结果,M A X—N个数据中的最大值,M IN—最小值。
经过多次实验比较发现,N取12比较合适。如果N取值过小,那么滤波的平滑效果不好;如果N取值过大,那么虽然滤波的平滑效果较好,但是数据处理速度变慢,不能满足设计要求。
本研究编写STM32的串口通信程序,并用串口连接到电脑,通过串口调试助手显示单片机从A/D转换器得到的数据。对传感器突然施加一个压力,模拟脉冲干扰后,可得到A/D转换器的读数,没有滤波算法的读数如图3所示,有滤波算法的读数如图4所示。
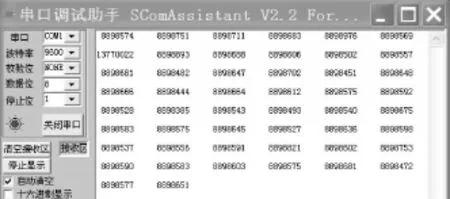
图3 突然施加压力时无滤波算法的读数
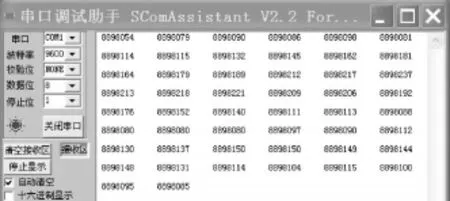
图4 突然施加压力时有滤波算法的读数
在图3、图4中,总共读数50个,每过500 ms读一次,在第2行第1个数据时,突然加一个压力在称重传感器上,然后,马上撤去压力,以此来模拟脉冲干扰。
从图中可以看到,在没有滤波算法时,第2行第1个读数,突然变大为13 770 022,在撤去压力后,经过大约读入5个数据后就恢复到以前的稳定读数。可见,在没有滤波算法时,读数的变化是陡变的。而在有滤波算法时,第2行第1个读数为8 898 114,比加压力前的读数8 898 081只增加了33,几乎没有变化。在撤去压力后,由于称重传感器的抖动等原因,使读数一度波动到最大值,第3行最后一个读数为8 898 237,但是,在经过大约读入12个数据后,又恢复到了以前的稳定水平,例如第5行最后一个读数为8 898 088。在整个过程中数据的波动范围不超过156(最大读数8 898 237减去加压力前的一个读数8 898 081),比没有滤波算法的波动范围4 871 453(加压力后的读数13 770 022减去加压力前的读数8 898 569)小了很多,而且,有滤波算法时,数据变化缓慢,对读数几乎没有影响。可见,改进后的滑动均值滤波算法有很好的拟制脉冲干扰的作用。
为了验证滑动均值滤波算法对短时间内多次脉冲干扰的滤波效果,以较快的速度对称重传感器连续施加4次较大的压力,可得到A/D转换器的读数,没有滤波算法的读数如图5所示,有滤波算法的读数如图6所示。
在图5、图6中,总共读数50个,每过500 ms读一次,在读第2行第1个数据时,较快地连续施加4次压力在称重传感器上,来模拟短时间内连续的多次脉冲干扰。
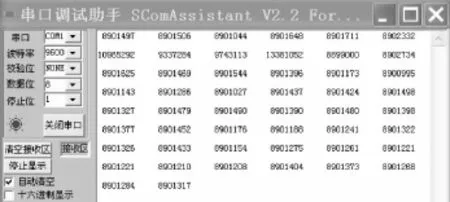
图5 连续施加4次压力时无滤波算法的读数

图6 连续施加4次压力时有滤波算法的读数
从图中可以看出,在没有滤波算法时,从第2行第1个读数开始,读数突然增大,连续出现了4个很大的读数,依次为10 965 292,9 337 284,9 743 113,13 381 052。在结束施加压力后,经过大约读入4个数据后就恢复到以前的稳定读数。可见,在没有滤波算法时,读数的变化是陡变的,而在有滤波算法时,第2行第1个读数为8 900 869,比施加压力前的读数8 900 839只增加了30,几乎没有变化。在结束施加压力后,由于这次施加压力的次数是4次,次数较多,在经过读入了29个数据后,才恢复到没有施加压力时的读数水平,例如,第6行最后一个读数为8 900 928。没有滤波算法时,由于施加压力而造成的数据波动范围是4 478 720(施加4次压力造成的4个很大的读数中最大的一个读数13 381 052减去施加压力前的读数8 902 332)。而有滤波算法时,数据波动范围是1 359 584(施加4次压力过程中造成的最大读数10 260 423减去施加压力前的读数8 900 839),比没有滤波算法的波动范围小了很多。但是,由于是连续施加4次压力,比施加1次压力有滤波算法时的数据波动范围还是大了很多。总的说来,在连续施加4次压力有滤波算法时,数据变化缓慢,对读数有较小的影响。可见,在短时间内发生多次脉冲干扰时,改进后的滑动均值滤波算法依然有较好的拟制脉冲干扰的作用。
4 实验结果
该设计的电子天平实物图如图7所示。

图7 电子天平实物图
该设计的电子天平要求最大允许误差小于等于0.02 g,根据《JJG 1036-2008电子天平检定规程》的检定要求,在20℃室温环境下,电子天平充分预热后,本研究采用精度为0.001 g的标准砝码对电子天平的重复性和示值误差进行了实验测试。
对载荷为200 g的砝码进行10次重复检定,电子天平重复性检定结果如表2所示。由表2可见,最大误差为0.02 g,满足设计要求。
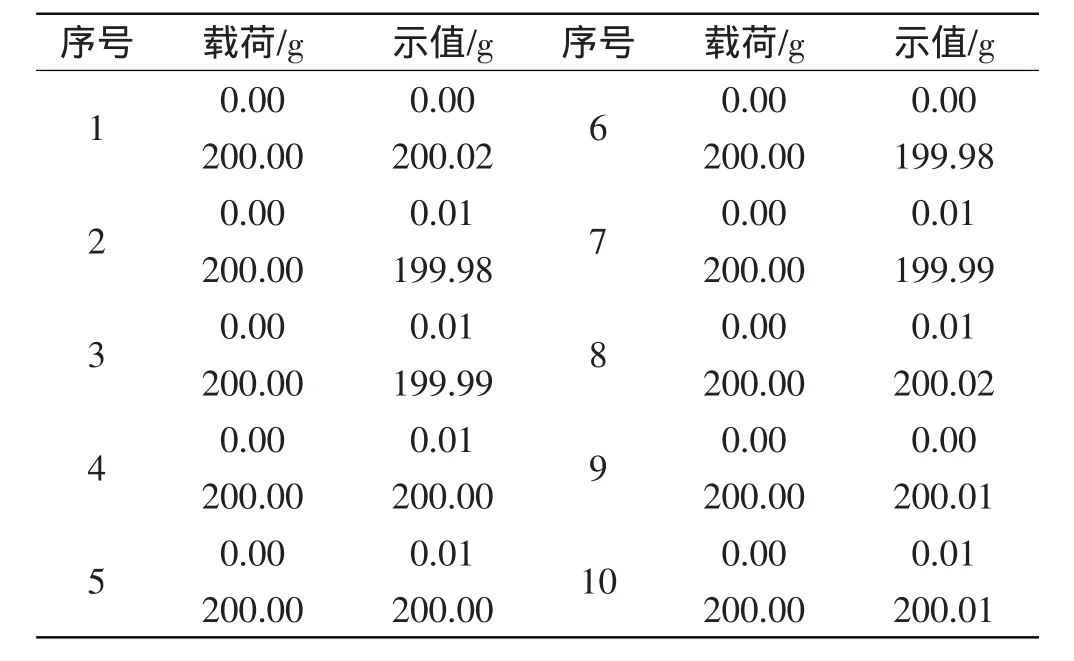
表2 重复性检定实验结果
电子天平示值误差检定结果如表3所示。本研究选取了0 g、5 g、10 g、20 g、50 g、100 g、150 g、200 g、250 g、300 g等10个不同的测量点。实验方法是:载荷从零开始,逐渐地往上加载,直至加到电子天平的最大称量,然后逐渐地卸下载荷,直到零载荷为止。由表3可见,电子天平的最大示值误差为0.02 g,满足设计要求。
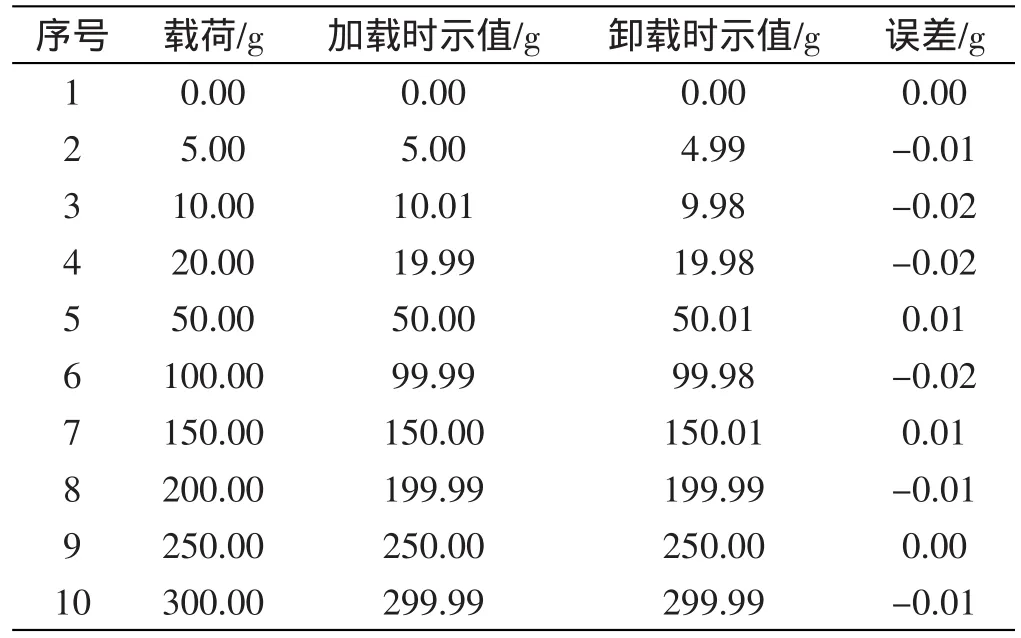
表3 示值误差检定实验结果
5 结束语
本研究对电子天平的基本工作原理进行了深入研究,并且通过调研发现目前市面上的电子天平精度较低、成本较高的问题。为此,本研究设计了一种基于STM32的高精度、低成本的电子天平,简化了电路连接,提高了电路的稳定性。大量实验结果表明,该天平设计量程为300 g,能够达到0.01 g的精度,误差小于等于0.02 g,称量速度快,10 s左右即可达到稳定读数,而且性能稳定、重复性好、准确度高。
但是,由于称重传感器和算法的原因,该设计的精度受到了限制。今后的改进中,研究者将使用精度更高的称重传感器和更优秀的算法,以进一步提高称量精度。
(References):
[1] 张民慧.电子天平显示值漂移问题的解决[J].衡器,2009,38(6):30-33.
[2] 杨 敏,滕召胜,陈良柱,等.CS5532的高精度电子天平设计[J].仪表技术与传感器,2010(1):14-18.
[3] 郭怀天,李宝华.基于电阻应变式称重传感器的电子天平的研制[D].长春:吉林大学电子科学与工程学院,2006.
[4] SLATTERY C,NIE M.A reference design for high-perfor⁃mance,low-cost weigh scales[J].Analog Dialogue,2005(12):1-6.
[5] 王盛奎,纪尚安,吴贺荣.小型电子称电路的研究[J].仪表技术,1999(6):31-33.
[6] GONZALEZ A G,HERRADOR M A.The assessment of electronic balances for accuracy of mass measurements in the analytical laboratory[J].Accreditation and Quality Assurance,2007,12(1):21-29.
[7] 马元群.智能型、大量程、精密电子天平设计[J].衡器,2009,38(8):42-44.
[8] 鲍丙豪,赵 湛,杨凯峰.基于厚膜力传感器的电子秤设计[J].仪表技术,2005(2):49-50.
[9] 苏堡莹,金 伟,曹建伟,等.高精度力传感器信号直接数字化技术研究[J].机电工程,2005,22(5):19-22.
[10] 朱亚萍,陈 伟,吴炎彪,等.标签检测抗干扰数字滤波方法研究[J].传感技术学报,2009,22(12):1722-1726.

