T形截面钢压杆整体稳定计算的折算长细比法

熊晓莉

(河南工业大学土木建筑学院，河南郑州450001)

0 引言

按照弹性稳定理论，T形截面压杆与其他单轴对称截面一样，当压力作用在截面形心时，构件绕其对称轴发生弯扭屈曲.而当压力作用在截面的剪切中心时，T形截面压杆绕其对称轴发生弯曲屈曲或扭转屈曲.自从上世纪六十年代开始，这一特点就逐渐广泛地被国内外研究人员所认识［1-4］.在 2004 年和 2007 年，陈绍蕃［1-2］提出了下述观点:T形截面压杆具有如下特性，即当压力由截面形心移至剪切中心时，其绕对称轴失稳时的承载能力将得到提高.然而，文献［5］进行ANSYS有限元分析后证明该结论不正确.

笔者从以下两方面进行研究:一方面，以我国《钢结构设计规范》(GB50017—2003)［6］的设计方法为基础，提出计算T形截面压杆设计承载力的新方法——折算长细比法，该方法与文献［1］中的方法和规范中的方法均有所不同;另一方面，既然T形截面压杆的设计承载力也能通过ANSYS有限元分析获得，笔者将对比新方法、文献［1］方法和规范方法的计算结果，证明新方法的合理性.

1 T形截面压杆的屈曲临界力

由弹性稳定理论可知，忽略对称轴平面内的失稳，如图1所示的T形截面的两端铰支轴心压杆绕其对称轴y轴发生弯扭屈曲，其屈曲临界力Pyz可由下式获得［1-4］

式中:i0为截面对剪心S的极回转半径=+;e0为截面形心至剪心的距离;ix，iy为截面绕x轴，y轴的回转半径;PEy为欧拉临界力，PEy=π2EIy/l2;Iy为截面绕 y轴的惯性矩;E为材料的弹性模量;l为杆件的计算长度;Pz为轴心压杆的扭转屈曲临界力，Pz=GIt;It为截面抗扭惯性矩;G为材料的剪切模量.

由式(1)可知，Pyz与 PEy和 Pz有关，且比二者中的任何一个都小.这表明剪心偏离形心导致压杆的临界荷载降低.

另一方面，压力作用于剪切中心的T形截面压杆绕对称轴y轴屈曲时弯曲变形与扭转变形不再耦合［1-4］，屈曲临界力有两个，一个为绕对称轴y轴屈曲时的欧拉临界力PEy;另一个为扭转屈曲临界力，由下式给出:

式中:βy为单轴对称截面的几何特性

式中:Ix为截面绕 x轴的惯性矩;A为截面面积;x，y为截面上任一点在形心主坐标系统(如图1)中的坐标.

由于e0与βy总是异号，根据式(2)和式(3)可知，Pzs总是比 Pz大，并且常比 PEy大.

如果压力作用点在截面形心与弯心之间的区域内，临界荷载Pyze由下式获得

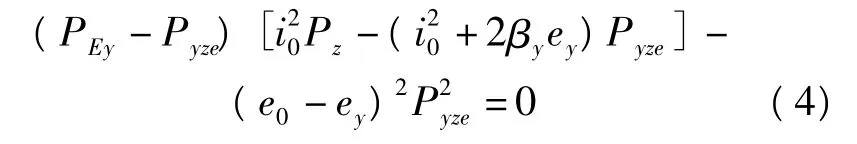
式中:ey为荷载的偏心距.

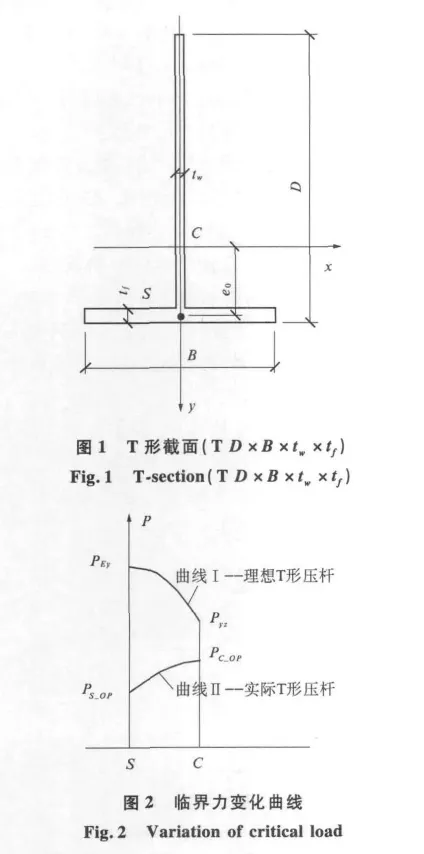
图2中的曲线I即为当压力由形心移至弯心的过程中，理想T形截面压杆的临界力变化曲线.

2 T形截面压杆设计计算的折算长细比法

T形截面压杆的临界荷载一般是针对弹性构件而言的.实际上，长细比λy=60的T形截面压杆绕对称轴y轴通常在弹塑性阶段发生失稳，其稳定设计承载力能通过折算长细比方法获得，该方法的实用计算公式是基于现行国家GB 50017—2003《钢结构设计规范》［6］提出的.

根据前述的屈曲分析内容，能获得压杆的屈曲临界力Pcr.对于轴心压杆而言，绕对称轴屈曲时的临界力 Pcr=Pyz.对剪心加载的压杆而言，平面外屈曲临界力Pcr=min(PEy，Pys)，平面内屈曲临界力 Pcr=PEx，其中:PEx为绕非对称轴 x轴的欧拉临界力.对一般的偏心加载压杆而言，平面外屈曲临界力Pcr=Pyze，平面内屈曲临界力Pcr=PEx.

可借助折算长细比的概念将弯扭屈曲问题转化为弯曲屈曲问题，折算长细比

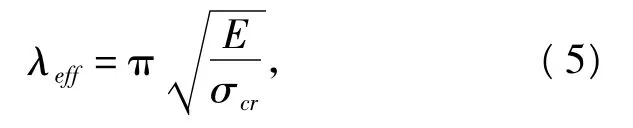
式中:σcr为T形截面压杆横截面上的屈曲应力，σcr=Pcr/Ac，Ac为偏心压杆的等效截面面积，Ac可由下式获得

式中:σn为压力P作用点处截面上的一阶应力.

根据现行钢结构规范中轴心压杆的正则化长细比公式，T形截面压杆的正则化长细比公式如下

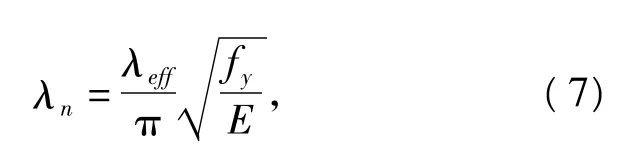
式中:fy为材料的屈服强度.

由规范中的柱子曲线(即φ-λ曲线，φ为稳定系数，λ为长细比)可知，T形截面压杆的柱子曲线表达式如下:

若λn≤0.215，曲线a的稳定系数

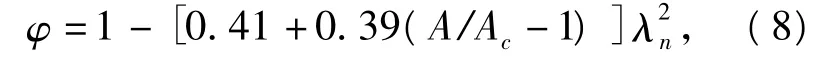
曲线b的稳定系数

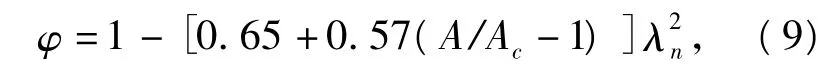
曲线c的稳定系数

若λn＞0.215，稳定系数

式中:ε0为等效偏心率，其表达式如下

曲线 a，ε0=0.152λn-0.014，

曲线 b，ε0=0.300λn-0.035，

曲线c，当0.215 ＜ λn≤1.05 时，ε0=0.595λn-0.094;当 λn＞1.05 时，ε0=0.302λn+0.216.

T形截面压杆的设计承载力

式中:f为材料屈服强度的设计值，f=fy/γR.

若不计T形截面压杆绕非对称轴的失稳，压力产生的弯矩作用在对称轴平面内的两端铰支T形截面压杆的设计承载力可由上述式(5)～式(12)计算获得.该方法对T形截面压杆稳定承载力的计算具有普适性，适用于轴心受压、剪心受压以及压力作用于截面轴心与剪心之间的任何情况.表1中列出了T形截面钢压杆(钢材屈服强度 fy=235 N/mm2，弹性模量E=206 000 N/mm2，剪切模量G=79 000 N/mm2)设计承载力的计算结果.

3 文献［1］中T形截面压杆的设计方法

文献［1］中，剪心加载的T形截面压杆设计承载力式中:φy为相应于长细比λy的稳定系数.

对轴心受压构件而言，借助换算长细比将弯扭屈曲问题转化为弯曲问题进行计算

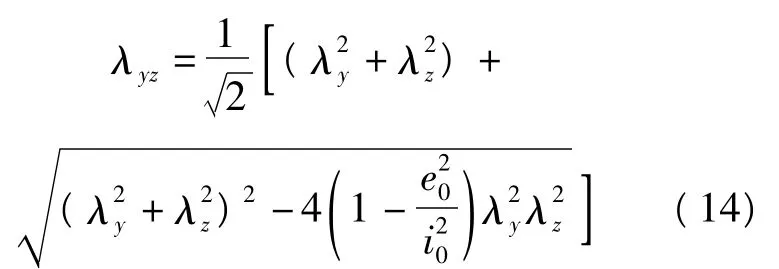
式中:λz为扭转屈曲时的换算长细比，=25.7A

轴心受压时的设计承载力

式中:φyz为相应于长细比λyz的稳定系数.

按照式(13)，(14)和(15)，T形截面压杆设计承载力的计算结果详见表1.

4 规范中的T形截面压杆设计方法

规范GB50017—2003中，轴心压杆设计承载力可由式(14)和式(15)获得.

对偏心压杆而言，设计承载力可由规范中的一系列公式获得.平面外稳定承载力可根据下式计算

式中:Mx为荷载偏心引起的绕非对称轴x轴的弯矩;W1x为截面最外边缘纤维处的抗弯模量;φb为杆件纯弯曲时的稳定系数，对T形截面压杆而

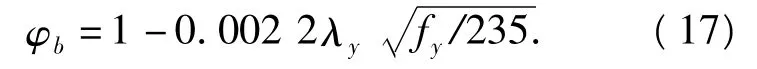
平面内的稳定承载力可由下式计算

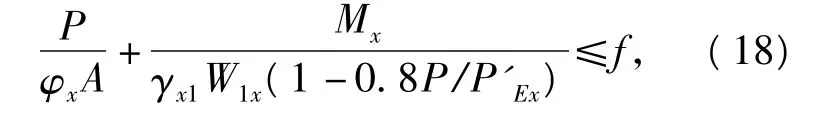
式中:φx为弯矩作用平面内的轴心受压构件稳定系数;γx1为截面塑性发展系数，对于T形截面受压翼缘而言，取 1.05;P’Ex为参数，P’Ex=π2EA/(1.1.

表1中列出了公式(16)，(17)和(18)的计算结果.

5 T形截面压杆弯扭屈曲的ANSYS分析

使用通用有限元程序ANSYS建立两端铰支的T形截面压杆的有限元模型，并对其进行非线性分析获得设计承载力，钢材的屈服强度取235 N/mm2，分析采用Von Mises屈服准则.

选取SHELL181单元，该单元为适用于线性、大转动和大应变分析的四节点单元［7-8］.

对材料属性的定义分为线性和非线性两部分.线性部分是在线性静力分析阶段之前进行定义的.定义杨式弹性模量E=206 000 N/mm2，泊松比v=0.3.非线性部分在非线性阶段定义，相应的应力应变关系曲线如图3所示.

建立几何模型.为正确模拟现实情况中构件两端的铰支约束，需要将构件两端部单元的弹性模量E修改为较大值.

定义边界条件，施加荷载，设定分析类型，选择静力分析，激活预应力开关后求解，然后，重新进入求解器，指定分析类型为特征值屈曲分析并求解，获得屈曲荷载和屈曲模态.

图3 应力—应变曲线Fig.3 Stress-strain curve

引入模型缺陷，如初始变形和如图4所示初始应力，定义材料的非线性，重新加载(加载大小约为屈曲荷载的50% ～80%)，设定分析类型为静力分析，打开大变形开关，选择弧长法，设置收敛准则，设置子步数，求解并获得非线性屈曲荷载.

图4 初始应力分布Fig.4 Distribution of initial stress

为证明新方法的正确性，表1中列出了一些T形截面钢压杆基于ANSYS的非线性分析结果.图2中的曲线II即为当压力由截面形心移至剪心时的设计承载力的变化曲线.

6 折算长细比法、文献［1］方法、规范方法与ANSYS的计算结果对比

在文献［1］和文献［5］中，对压力作用在剪心、形心和形心与剪心之间的M点(CS中点)时T形截面压杆的承载力大小进行了对比.表1中列出了对T248×199×9×14和 T298×199×10×15压杆分别按照新方法(折算长细比法)、文献［1］方法、规范方法、ANSYS方法的计算结果.

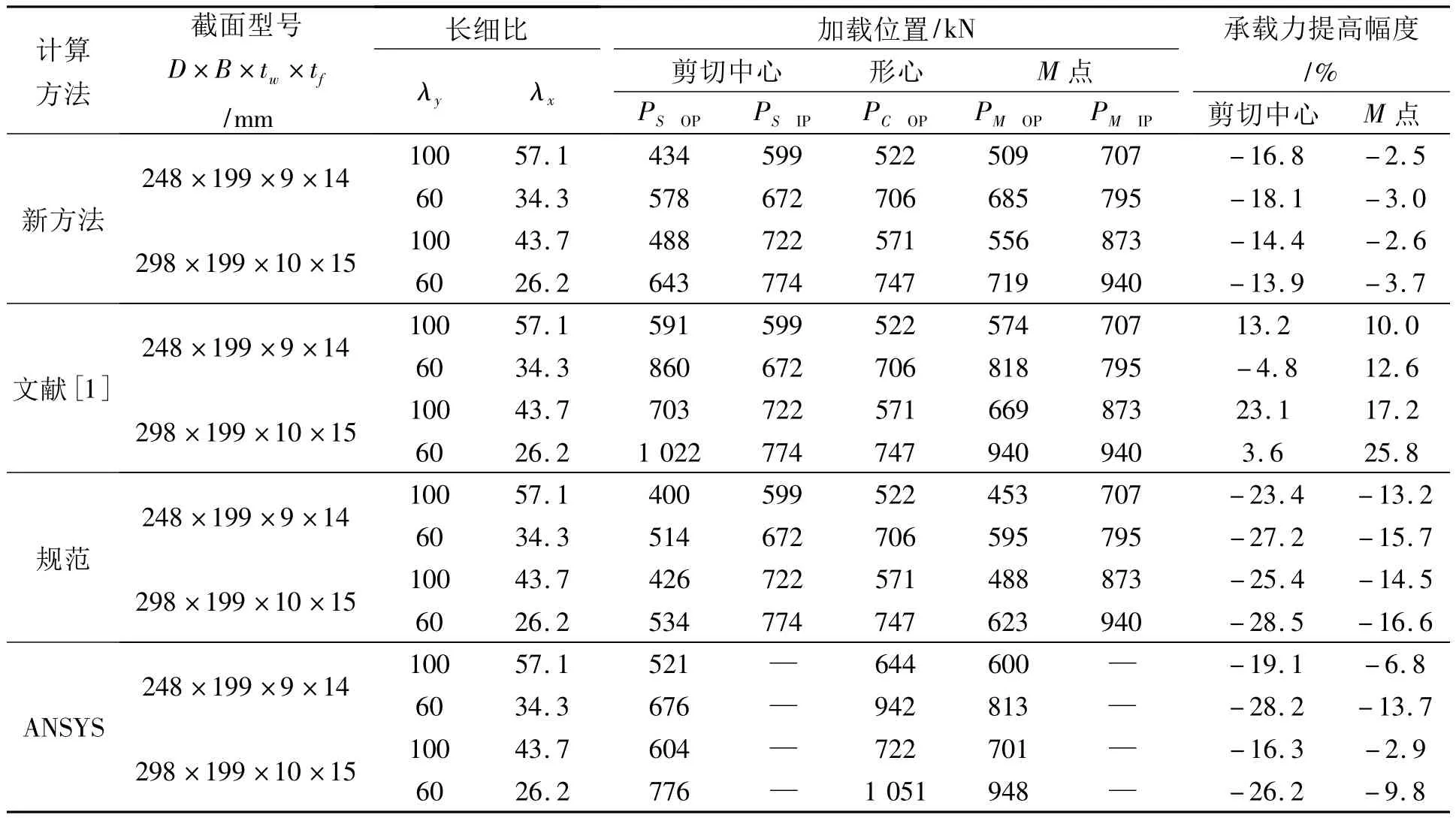
表1 压力作用在不同位置时T形截面压杆承载力计算结果对比Tab.1 Comparison of T-strut capacity subject to loading at different positions

文献［1］中数据表明，当压力由形心移至弯心或M点时，构件的承载力将有所提高.文献［1］按照其中提出的计算方法，在计入截面弯角部分面积的条件下得到了T形截面钢压杆的稳定承载力.为了将其与笔者提出的折算长细比法、规范方法和ANSYS的计算结果(均未计入截面弯角部分面积)进行比较，表1中所列出的文献［1］中数据为按照其提出的计算方法，在不计入截面弯角部分面积的条件下得到的计算结果.因此，与文献［1］中的原数据略有不同，但差别不大.

由于ANSYS模型更贴近实际情况，而新方法和规范中的计算公式均偏于安全，ANSYS的计算结果大于新方法和规范的计算结果.并且，新方法的计算结果与ANSYS的计算结果更为贴近.新方法、规范方法以及ANSYS方法中的计算结果均表明:荷载的偏心将导致压杆承载力的下降.

由表1中的数据可知，文献［1］中的计算方法有误，原因是:按照式(13)计算剪心加载的T形截面压杆的设计承载力是不合理的，该式仅适用于双轴对称截面和极对称截面压杆承载力的计算.因而，在桁架设计中，不能按照文献［1］的建议将压力作用线由T形截面压杆的形心轴移至剪心轴.

虽然ANSYS的非线性分析结果更接近实际，但由于有限元模型的建立过于复杂而不便于应用.因此，基于上述4种方法的对比分析结果，建议对T形截面压杆进行稳定承载力计算时采用折算长细比法.

7 结论

在弹性阶段，无缺陷的的T形截面压杆绕其对称轴屈曲时，当压力由截面剪切中心移至形心时，其屈曲荷载将会降低.然而，在弹塑性阶段，有初弯扭、初偏心及残余应力等初始缺陷的T形截面压杆绕其对称轴屈曲时，当压力由截面剪切中心移至形心时，其屈曲荷载将会提高.

介绍了4种计算T形截面压杆设计承载力的方法，特别提出了一种新方法——折算长细比法，并将该方法与陈绍蕃提出的计算方法、规范中的计算方法以及有限元法进行对比后指出新方法合理、简捷，值得推广应用.

［1］CHEN Shao-fan.Buckling of T-strut subject to compressive force on its shear center［J］.Journal of Constructional Steel Research，2007，63(3):332-336.

［2］陈绍蕃.剖分T型钢压杆的屈曲性能和应用［J］.建筑钢结构进展，2005，7(4):1-5.

［3］TIMOSHENKO S P，GERE J M.Theory of elastic stability［M］.New York:McGraw-Hill，1961.

［4］CHEN W F，Atsuta T.Theory of Beam Columns［M］.New York:McGraw-Hill，1977.

［5］XIONG Xiao-li，JIN Lin-bin，WANG Hui.Design capacity of T-strut subject to compressive force［J］.Advanced Material Research，2011，(163/167):550-556.

［6］中华人民共和国建设部.GB 50017—2003钢结构设计规范［S］.北京:中国计划出版社，2004.

［7］ANSYS Inc.ANSYSRelease 9.0Documentation［CP］.USA，2004.

［8］彭晓彤，陈绍蕃，顾强.剖分T型钢压杆的弯扭屈曲试验研究［J］.建筑结构学报，2004，25(2):44-48.