空船压载状态优化计算的数学模型

邱文昌，张春燕，周云薇

(上海海事大学商船学院，上海 201306)

0 引言

散装液货船(油船、液化气体船和液体化学品船)和矿砂船几乎有一半航程在空船压载状态下航行，其他类型的船舶在营运中也常会遇到空船压载下航行的情况.因此，研究各类船舶在不同海况下的空船压载优化方案，对减小船舶阻力、提高船舶快速性和耐波性、实现船舶节能增效目标具有重要的意义.［1］

习惯上，多数船舶在空船状态下采用本船《装载手册》中所推荐的压载方案(简称推荐方案).实际上，推荐方案提供的压载状态常常在满足船舶浮态、稳性和纵强度要求下，多数压载舱满载或接近满载，适合船舶在限定航区各种海况下航行，但推荐方案并非是特定海况下的最佳方案.

本文在兼顾船舶浮态、稳性和总纵强度要求下，设计算法并建立求解船舶优化压载方案的多目标数学模型，借助LINGO编程给出一个求解空船优化压载方案的计算实例.

1 空船优化压载方案的求解算法和模型

1.1 船舶浮态、稳性和纵强度要求

空船优化压载方案不但应满足船舶浮态、稳性和纵强度的最低要求，而且应同时优化船舶浮态、稳性和纵强度的指标值，并使压载水的总量相对较小.

1.1.1 浮态

船舶在同一排水体积下处于不同的浮态，直接影响水下流线型船体的形状和船体浸水面积，从而影响船舶的水下阻力.

对于最小艏吃水dFmin，上海船舶运输科学研究所在分析国际海事组织(International Maritime Organization，IMO)浮态衡准后提出建议［2］为

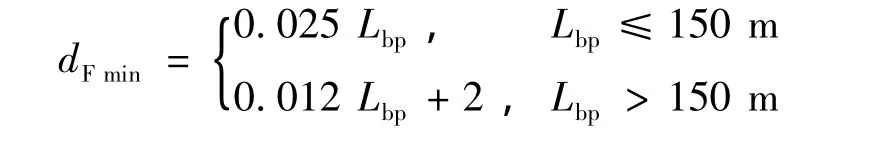
式中:Lbp是船舶垂线间长.该项要求是为保持船舶球鼻首适度浸入水中，可以改善船体水下的流线型形状、降低船舶兴波阻力等.

最小艉吃水 dAmin应满足使螺旋桨沉深比h/D≥0.625的要求，保证船尾螺旋桨浸没水中一定深度，以提高螺旋桨的推进效率.

空船压载状态下通常要求吃水差

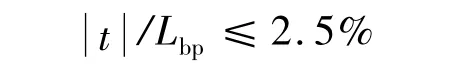
船舶在空载状态下的平均吃水同时还影响到水线以上船体的受风面积和水线以下船体的浸水面积.不同海况(特别在恶劣海况)下万吨级船舶的最小平均吃水dMmin通常要求超过其夏季满载吃水50%.上海船舶运输科学研究所提出建议为

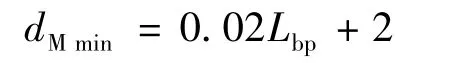
笔者认为，大型船舶在海况良好时可适度减少船舶平均吃水，以降低船舶阻力、增加航速.

船舶在任一装载状态(包括空载)下，应满足无初始横倾角的要求.

1.1.2 稳性和纵强度

在空船压载下船舶稳性通常都能满足法定要求，但许多船舶在空载时的重心偏低，初稳心高度偏

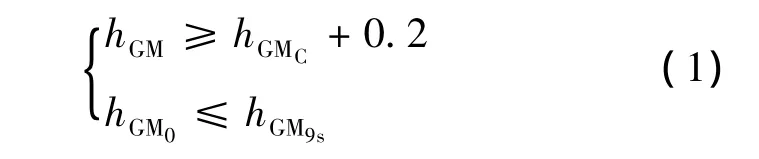
式中:hGM和hGM0分别为船舶经自由液面修正和未经自由液面修正的初稳心高度，m;hGMC和hGM9s分别为船舶最小许用初稳心高度和横摇周期9 s对应的船舶初稳心高度，m.船舶某浮态下的初稳心高度在满足式(1)的条件下取优化值(可由软件用户修改)

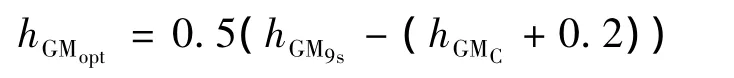
在空船压载下船舶纵强度通常也能满足要求，但在空船压载方案的求解中其纵强度指标存在较大的优化余量.设定具体的船体纵强度校核指标为:船舶每一校核纵强度的横剖面上的切力比和弯矩比中最大值不大于100%，期望值小于50%;其各切力比和弯矩比的平均值不大于100%，期望值小于10%.

1.2 空船优化压载方案的算法

空船优化压载方案的算法［3－5］如下:

(1)获取船舶相关压载舱容积、压载水密度、船体纵强度等数据.若设船舶共有nt个压载舱，其舱容分别为 V1，V2，…，Vk，…，Vnt，压载水密度为 ρ，则各压载舱的最大压载质量为mPmax1，mPmax2，…，mPmaxk(=Vk·ρ)，…，mPmaxnt;设船体强度校核ns个剖面最大允许切力值为 FSmax1，FSmax2，…，FSmaxi，…，FSmaxns，nb个剖面最大允许弯矩值为 MBmax1，MBmax2，…，MBmaxi，…，MBmaxnb.

(2)设置船舶初始压载状态.借助船舶装载软件，在某油水装载状态下，调整船舶各压载舱的初始压载质量(设初始压载质量为 mP01，mP02，…，mP0k，…，mP0nt)，使之满足船舶浮态要求(dF≥dFmin;dA≥dAmin;吃水差t等于设定最佳值topt(即t=topt);横倾角θ等于0(即θ=0)下，使船舶排水量mΔ达到其最小值 mΔmin(即 mΔ=mΔmin).

(3)确定船舶各压载舱压载质量取值范围.设mPmaxk为第k压载舱最大压载质量，它等于第k压载舱舱容与压载水密度之积;设ΔmPk为在初始压载状态下第k压载舱压载质量的改变值，则

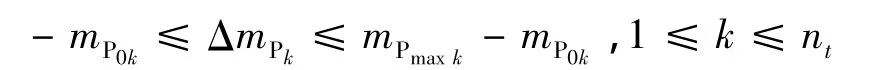
(4)初始压载状态下获取船舶切力、弯矩和吃水差，以及加载100 t船舶切力、弯矩和吃水差改变值.即获取ns个强度校核剖面剪切力值FS01，FS02，…，FS0i，…，FS0ns;nb个强度校核剖面弯矩值 MB01，MB02，…，MB0i，…，MB0nb;各压载舱加载100 t每一纵强度校核剖面剪切力改变值、弯矩改变值和吃水差大而摇摆周期偏小，需要在确定空船压载方案时予以考虑.设定船舶稳性指标要求为改变值(如第k压载舱剪切力改变值ΔFSk1，ΔFSk2，…，ΔFSki，…，ΔFSkns，弯矩改变值 ΔMBk1，ΔMBk2，…，ΔMBki，…，ΔMBknb和吃水差改变值 Δtk).

(5)借助数学模型(第1.3节)和LINGO编程并运行程序，求解船舶优化压载方案.船舶的优化压载质量为:mP01+ΔmP1k，mP02+ΔmP2k，…，mP0k+ΔmPkk，…，mPnk+ΔmPnk.

(6)将求解的优化压载方案输入装载软件进行验算.即将第5步的优化压载质量输入装载软件，以获取装载软件的计算结果.

(7)比对数学模型求算结果和船舶装载软件计算结果.①检查装载软件计算结果中船舶横倾角是否接近0，艏艉吃水、吃水差和排水量是否均达到设定的浮态要求值，核查船舶初稳心高度hGM是否满足设定要求.②将数学模型求算结果中各强度校核剖面的剪切力比及弯矩比数据与船舶装载软件的相应计算结果进行比对.

(8)若对第7步比对结果不满意，则调整数学模型中的权重或由优化方案给出的某舱实际压载的改变量，修改加载100 t船体剪切力、弯矩或吃水差改变值，再转至第5步.

(9)若对第7步比对结果满意，则算法结束.

1.3 数学模型

空船状态下通过压载水调整船舶纵倾(吃水差)和横倾的目标易于达到，因此将该两项指标置于模型的约束条件内.鉴于通过压载水调整船舶纵强度和稳性指标的难度较高，常常会出现顾此失彼现象，所以将其组合后置于数学模型的目标函数中.

空船优化压载方案的数学模型［6］中的目标函数为

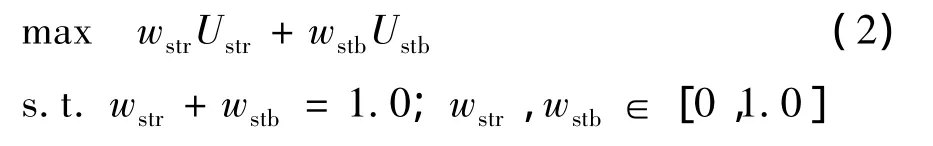
式中:wstr为纵强度效用值权重;wstb为稳性效用值权重.

定义纵强度效用值为

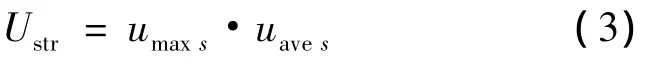
纵强度剪切力比和弯矩比(即船体某剖面实际剪切力或弯矩占其最大允许值之百分比)最大值PRSBmax的效用值被定义为

定义纵强度剪切力比和弯矩比平均数PRSBaves效用值为

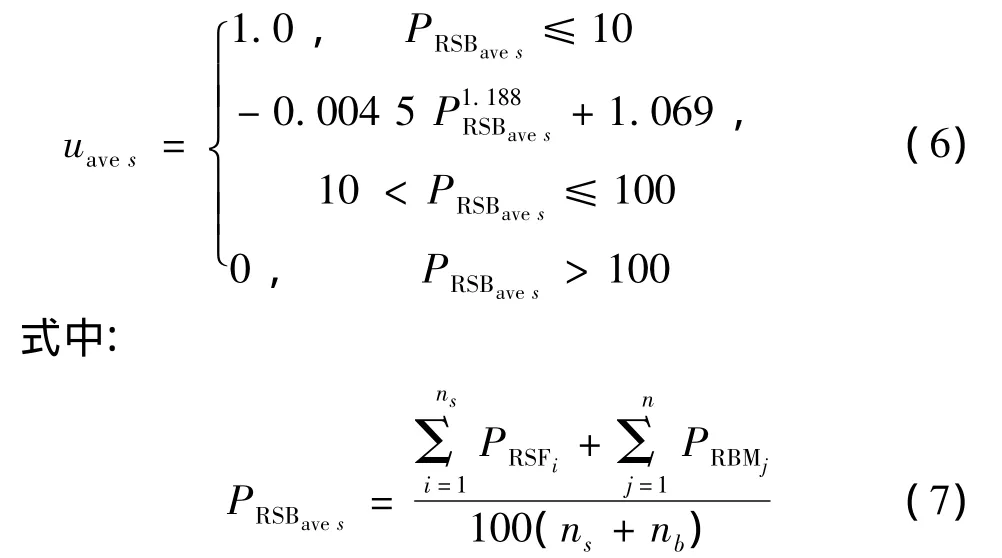
第i剖面剪切力比

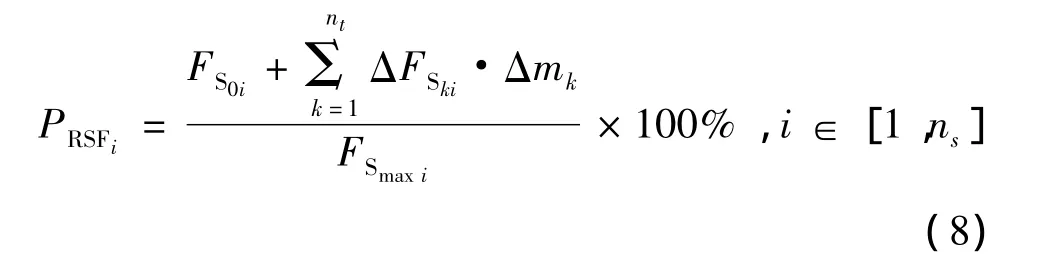
第j剖面弯矩比

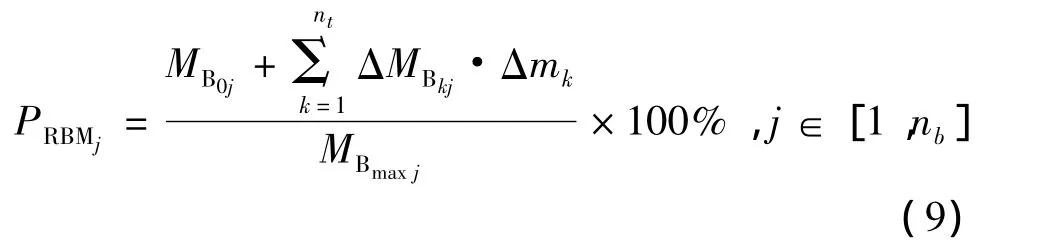
定义船舶稳性调整的效用值为

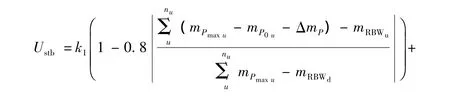
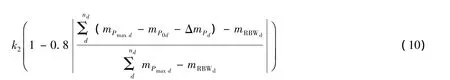
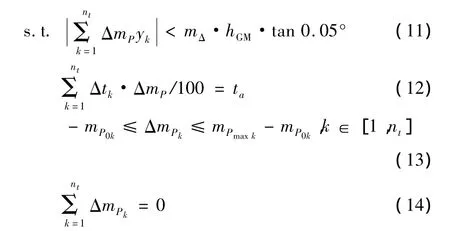
式(2)中权重wstr和wstb用于反映对船体纵强度和稳性评价中的相对重要程度，需要依据不同船舶空船时纵强度和稳性的实际状况或偏好确定;Ustr和Ustb是船体纵强度评价效用值和船舶稳性评价效用值，取值范围［0，1］.

式(3)中umaxs和uaves是船体强度各校核横剖面剪切力比和弯矩比(式(8)和(9))中最大值(式(5))和平均值(式(7))的效用值，其取值范围［0，1］，计算公式见式(4)和(6).根据船舶纵强度校核横剖面剪切力比和弯矩比最大值PRSBmax和平均值PRSBaves的实际状况，两者均不可能等于0，而当两者之一超过100时，其效用值umaxs和uaves即为0.从式(3)可知，若umaxs和uaves两者之一取0，则纵强度效用值Ustr为0，也即意味着纵强度不满足要求.

式(4)是设定当校核强度剖面的剪切力比和弯矩比的最大值的效用值PRSBmax≤50%时，其效用值取1;PRSBmax＞100%，则取 0;当 PRSBmax在 50% ～100%之间时，依据前段PRSBmax在50% ～90%之间较平坦，后一段 PRSBmax在90% ～100%之间较陡峭，PRSBmax为90%的效用值取0.7(采用MATLAB拟合曲线方法获得效用值计算公式).

式(6)是设定当校核强度剖面的剪力比和弯矩比平均值的效用值PRSBaves≤10%时，其效用值取1;PRSBaves＞100%，则取0;当 PRSBaves在10% ～100%之间时，依据设定接近直线的上凸曲线(采用MATLAB拟合曲线方法获得效用值计算公式).

式(7)，(8)和(9)中设定的符号与前述算法中一致.其中，式(8)和(9)建立的条件是在船舶浮态不变条件下，将船上少量载荷纵向位置改变引起的每一剖面上剪切力和弯矩改变量近似看作呈线性关系［3］.

式(10)为调整船舶稳性的效用值计算公式，式中:下标 u={C1|1，2，…，k，…，nt}，其中，设定 C1条件为压载舱中舱容中心高于船舶重心高度时压载舱编号集合;下标 d={C2|1，2，…，k，…，nt}，其中，设定C2条件为压载舱中舱容中心低于船舶重心高度时压载舱编号集合.式(10)系数取0.8是考虑当上或下层压载舱只配置50%压载水时设置的效用值为0.6.mRBWu和mRBWd分别表示舱容中心高于和低于船舶重心高度时压载舱的最大压载量之和与船舶总压载量的差值，当前者小于后者时取0.k1和k2是船舶重心高度调整系数，当期望提高船舶重心高度时，取k1=1，k2=0;当期望降低船舶重心高度时，取k1=0，k2=1;当不需要考虑船舶重心高度的调整时，取 k1=0，k2=0.

式(11)中yk表示第k压载舱重心横向距船中纵剖面距离，左舷取负值，右舷取正值.不等式右边表示导致船舶横倾0.05°时所需横倾力矩.由于所设置的船舶初始浮态已满足船舶横倾角为0，满足该式即表示优化压载方案能够保证船舶初始横倾角不大于0.05°.

式(12)左边表示第k压载舱压载量的改变值Δmk乘以其加载100 t吃水差改变值Δtk之后除以100，右边表示期望的吃水差topt与将优化压载方案输入装载软件后获得的吃水差之间差值ta.ta值初始取0，将优化压载方案输入装载软件后，若计算结果中显示的吃水差tc≠topt，取ta=topt－tc，需再次求解优化压载方案.

式(13)表示在船舶初始压载方案基础上，各压载舱可供调整压载量的上下限.

式(14)表示与船舶初始压载方案相比，各压载舱压载量的改变值之和为0，即保证优化压载方案满足 mΔ=mΔmin的要求.

2 空船优化压载方案的计算实例

为验证算法与模型，尝试采用LINGO编程［7］，以德国SEACOS GmbH公司开发的SEACOS V3.21装载系统为验证平台，完成一个SEACOS V3.21装载软件演示版中所包含的一艘典型9个货舱22个压载舱尾机型散货船(资料见表1和2)的空船优化压载方案的实例计算.

2.1 设定的船舶初始压载状态

船舶初始压载状态需要满足其浮态与优化压载状态相同这一条件.设置初始压载状态的目的是为保证某压载舱改变压载量时，仅引起载荷重力分布发生变化而船体水下浮力不变.经装载软件测试表明，在此条件下船上载荷的变化量与某强度校核剖面上的剪切力与弯矩近似成正比.此外可以证明，在船舶排水量不变的条件下，船上载荷变化量与船舶吃水差变化量成正比.

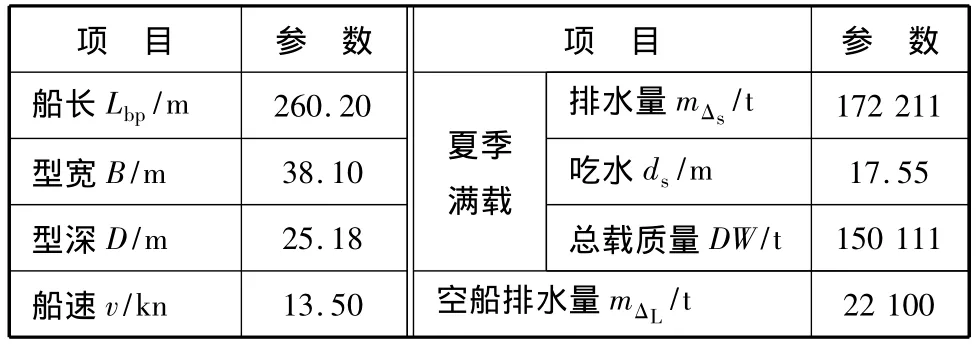
表1 M.V.“Seabulk”主要参数1

表2 M.V.“Seabulk”主要参数2

设定初始压载状态下的船舶浮态是:艏吃水为dF=0.012Lbp+2=5.12 m，按螺旋桨沉深比取0.65确定艉吃水为dA=9.27 m，吃水差t=－4.15 m(满足其绝对值与船长之比小于2.5%的要求)，船舶初始横倾角等于0°.由此确定的船舶平均吃水为7.04 m(排水量62845.2 t)，小于《装载手册》推荐方案的8.28 m(排水量75121.7 t).船舶离港状态下油水装载情况为:燃润油2247 t，淡水949 t，船舶常数和备品350 t.装载软件显示，经对各压载舱反复调整压载量后其浮态能够满足设定要求，总量37199 t压载水在各舱分布见表3.在初始压载状态下各压载舱经加载100 t载荷后获取船体纵强度和吃水差数据，见表4.

表3 初始压载方案各舱压载质量

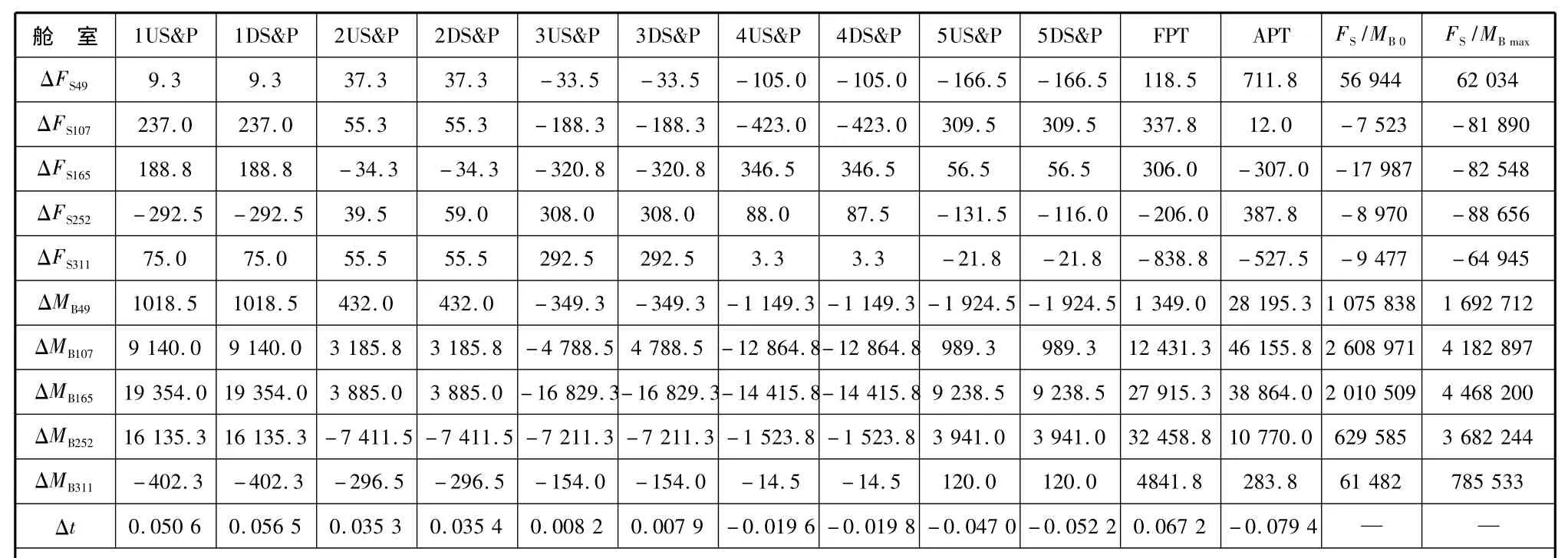
表4 每加载100 t各横剖面剪切力、弯矩和吃水差变化量

2.2 数学模型的求解

基于LINGO 12.0编程求得的优化压载方案见表5.初始压载状态下船舶重心过低，初稳心高度偏大，因此取k1=1，k2=0.由表2可见，压载舱中舱容中心高于船舶重心高度的压载舱编号集合包括5个上边舱1US＆P，2US＆P，3US＆P，4US＆P，5US＆P 和尾尖舱APT.式(10)中定义的mRBWu=0(因上述共11舱最大装载量22101.3 t小于压载总量37199 t).

经LINGO两次解算和装载软件验算获取ta为0.16 m，船舶初始横倾角为0，以及纵强度校核指标LINGO解算值和装载软件验算结果以及两者间误差见表6.为简化起见，仅给出5个肋骨数据)，其最大绝对误差为－2.7，绝对平均误差为－0.91.经对数学模型的多次解算结果的比较，并考虑到压载方案对船舶稳心高度的调整余量较小，在实例计算中wstr取 0.7，wstb取 0.3.

表5 LINGO解算的优化压载方案

表6 纵强度指标的计算误差

2.3 优化压载方案与推荐方案的比较

由模型解算获得的优化压载方案所确定的船舶重心垂向高度由初始压载方案的11.14 m(推荐方案为11.74 m)提高到12.79 m，船舶横摇周期相应提高近1 s，达到8.9 s.显然，在优化压载方案下船舶的稳性有一定程度改善.而采用优化压载方案对船舶纵强度指标的改善效果也非常明显(见表7)，推荐压载方案的剪切力比和弯矩比中最大值是94.8%，优化压载方案是91.9%，推荐压载方案的剪切力比和弯矩比平均值是51.6%，优化压载方案仅为30.9%.

表7 两种压载方案的纵强度评价指标比较

另外，将同一艘船的优化压载方案与船舶《装载手册》推荐的压载方案进行比较，仅存在吃水差和平均吃水两方面的差异，符合运用海军系数法［8］要求的两船主尺度比、船型系数、型线形状以及相应速度比较接近的条件，因此可以运用海军系数法估算同一船两种压载状态下主机功率消耗和船速.优化压载方案与推荐压载方案因前者压载水比后者减少12276.5 t，采用海军系数法的估算结果是:相同船速下优化压载方案的主机功率消耗减小11.2%;在相同主机功率消耗下，船速提高4.0%.

3 结束语

目前，国内外各类规则对空船压载状态下的船舶平均吃水并无强制要求，本文给出一种理论上的空船优化压载方案计算方法.此方法可扩展应用于确定各类船舶在任一装载状态下的优化压载方案中.对于特定船舶，应当存在一个随船舶油水消耗和海况不同而动态变化的，能使船舶总阻力最小、船速最快的最佳压载方案.这种方案需要船舶驾驶人员针对不同船舶装载状况和海况，通过多次调整船舶压载方案改变船舶不同纵倾和平均吃水后获取.显然，采用优化压载方案的船舶在航行中如遇恶劣海况时，还是应降低船速，适当增加船舶平均吃水，或采用《装载手册》中推荐的压载方案.

［1］邱文昌，吴善刚.对船舶最佳压载方案编制问题的研究［J］.上海海运学院学报，2001，22(2):4－8.

［2］邱文昌，吴善刚.海上货物运输［M］.大连:大连海事大学出版社，2010:187－193.

［3］邱文昌，顾瞿飞.散货船优化积载的数学模型及其应用［J］.上海海事大学学报，2011，32(4):22－27.

［4］尹群，管义锋，张延昌.船舶静水剪力和静水弯矩的计算及分析［J］.造船技术，2002(1):11－14.

［5］邱文昌，吴善刚.装载计算机操作中改善船体受力状况的方法［J］.上海海运学院学报，1998，19(2):32－40.

［6］吴善刚，邱文昌.大型集装箱船的总纵强度实用计算方法［J］.上海海运学院学报，1998，19(3):51－56.

［7］谢金星，薛毅.优化建模与LINDO/LINGO软件［M］.北京:清华大学出版社，2005:105－130.

［8］盛振邦，刘应中.船舶原理［M］.上海:上海交通大学出版社，2003:289－190.