供需平衡的集装箱船舶最大载箱量

赵梦梦，陈国庆，赵一飞，李南南

(1.上海交通大学a.船舶海洋与建筑工程学院;b.安泰经济与管理学院，上海 200240;2.中航商用航空发动机有限责任公司，上海 201108)

0 引言

自1956年泛大西洋轮船公司开创世界集装箱运输的新纪元以来，集装箱运输以其特有的便捷、安全、廉价和高效等优越性备受广大客户的青睐.随着经济全球化的不断深入，全球集装箱海运量持续上升.虽然2008年的金融危机对全球贸易产生巨大冲击，但是2004—2011年的世界集装箱贸易量仍以年均6.89%的速度递增(图1).

图1 1996—2011年世界集装箱贸易量

在全球航运市场普遍低迷的环境下，集装箱贸易量的持续增长对班轮公司无疑是极大的激励.为应对日益激烈的市场竞争，班轮公司积极加快集装箱船舶大型化的步伐［1］，2006年马士基班轮公司用“艾玛·马士基(Emma Maersk)”号重新定义集装箱船的最大载箱量.

目前，全球载箱量超过10000 TEU的巨型集装箱船(Very Large Box Carrier，VLBC)总数并没有因为全球金融风暴而停止增加的步伐，2012年底又有60多艘船舶被投入远东欧洲航线以及太平洋航线.［2］更有甚者，2011年2月，马士基班轮公司给出30艘18000 TEU集装箱船的订单.图2为1996—2011年全球集装箱船舶载箱能力增长情况.面对这一现实，全球班轮界必须思考:集装箱船舶的大型化将按照怎样的规律演变?

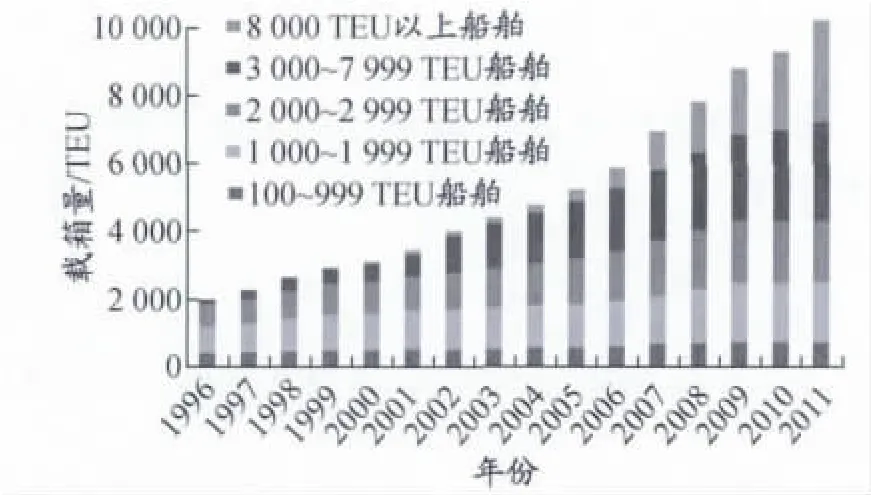
图2 1996—2011年全球集装箱船舶载箱能力增长情况及构成变化

赵一飞［3］从船舶规模和港口、航道等技术限制出发，对集装箱船型规模进行预测，认为5000 TEU以上的集装箱船舶从建造角度看技术难度可以突破，但是从航行和经济可行性角度看存在较大的不确定性.IMAI［4］概述超大型集装箱船的基本特征.CULLINANE等［5］分析典型航线上不同船型的单位经济成本，以及未来船舶大型化趋势对集装箱营运、物流系统及码头的影响.CULLINANE等［6］对超大型集装箱船的可行性作进一步研究.仇鑫尧［7］讨论可行的主尺度、航速等设计参数，以利润为目标，以费用－效益分析方法对中远发展7000 TEU集装箱船进行技术可行性分析和论证.吴冲［8］对集装箱船舶大型化的规模经济效益优势进行分析，建立集装箱船舶运输成本模型，对不同规模集装箱船舶的成本差异进行相对评价.张仁颐［9］给出在航线上货运量已知条件下集装箱船舶最大载箱量的计算方法.BRANCH等［10］从全球适箱货贸易增长的周期性出发，表示出对VLBC发展速度的担忧.以上对集装箱船大型化的研究基本立足于船舶经济性和技术可行性等方面，他们的预言多数都被业界的实际发展状况所突破.

1 集装箱船大型化和巨型船舶的概念

集装箱船舶大型化趋势有两个含义:一个是集装箱船舶平均箱位的增长;另一个则是船舶最大载箱量的提高.20世纪60年代，集装箱船的平均箱位运力不足300 TEU;到20世纪70年代末，这一数字迅速上升到620 TEU;据德国航运经济与物流研究所统计，20世纪80年代末达到 1200 TEU;据CLARKSONS统计，1995年末世界集装箱船单船平均运力1500 TEU，到20世纪末该数字进一步增加到1756 TEU;截至2012年9月1日，世界集装箱现役船队的平均运力已达到3134 TEU，船舶大型化已是集装箱船队发展的主流.［11］

关于集装箱船的最大载箱量，航运界与造船界的认识不同.1982年底，在荷兰鹿特丹举行的讨论会上，西班牙的造船专家们提出一种预计可装运3400只40英尺集装箱(或6800只20英尺集装箱)的集装箱船设计方案，在当时被称为巨型集装箱船.随着造船技术的不断发展，2005年集装箱船的最大载箱能力增长到8000 TEU.到2011年，载箱量18000 TEU的船已经开始建造，根据建造进度，这些船舶应该在2013年投入运营.

导致上述变化的原因无疑是全球贸易的增长.但是有关全球贸易与船舶大型化趋势关系的研究，大多建立在定性分析以及数量的相关性分析基础上，尚未有人给出明确的算法和结论.本文试图基于供需平衡理论探讨全球集装箱贸易量与集装箱船最大载箱量之间的关系，以帮助班轮公司确定最大载箱量的船舶投入市场的时间，对于班轮公司的投资决策具有重要意义.

2 建模

假设全球集装箱贸易量稳定增长，各大班轮公司的新造船投资都是理性的，即每家班轮公司的造船计划均是根据航线增长计划制订的，而航线增长计划又是由航线两端港口之间的贸易增量决定的，针对基于集装箱船舶运力供给与全球集装箱贸易量供求平衡的情况可以进行如下分析.

设t年度集装箱船舶的最大载箱量为Yt，该年全球集装箱贸易量为Tt，两个变量之间的关系可表示为

式(1)中，Tt是自变量，它主要随全球GDP的增长率、主要经济体的货币发行量、利率以及主要货币之间汇率的变动而变动，但Yt的大小对其只是约束作用.反过来，Yt与 Tt正相关，Tt越大，Yt就越大;但是Tt一旦变小，Yt却保持在Tt最大值时的数值上，一般不会同步下降.

为找出Yt与Tt的函数关系，首先要取得分析期各年份的Yt和Tt，见表1.

表1 分析期各年份的集装箱船最大载箱量和相应的集装箱贸易量

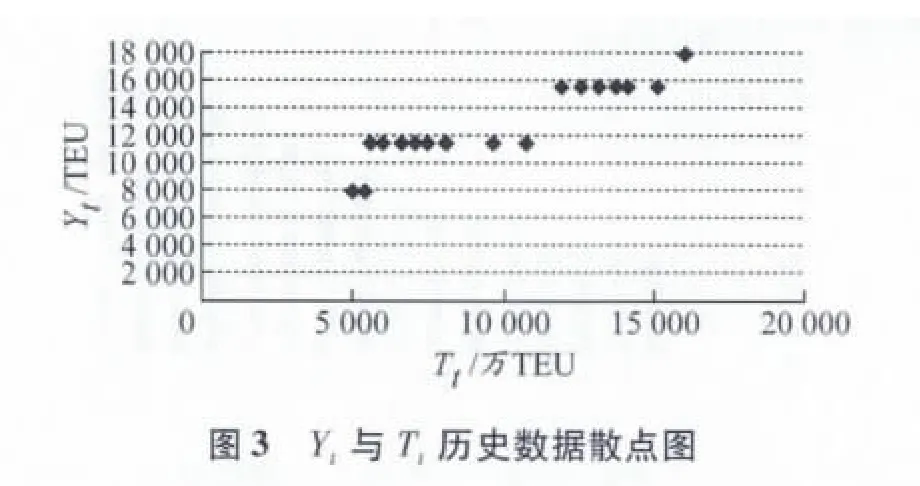
求解此类问题通常都会采用回归方法寻找二者之间的函数关系.［12］但是从运用表1的数据所作的散点图(图3)可见，Yt与Tt之间不存在显著的函数关系.显然，回归方法不适合解决此类问题，必须另辟蹊径.

根据国际海事组织(International Maritime Organization，IMO)公布的1996—2012年间各年度集装箱船队的数据，可以作出如图4所示的曲线族，其中纵轴为船舶的载箱量yt，横轴是对应一定载箱量的船舶数量nt.

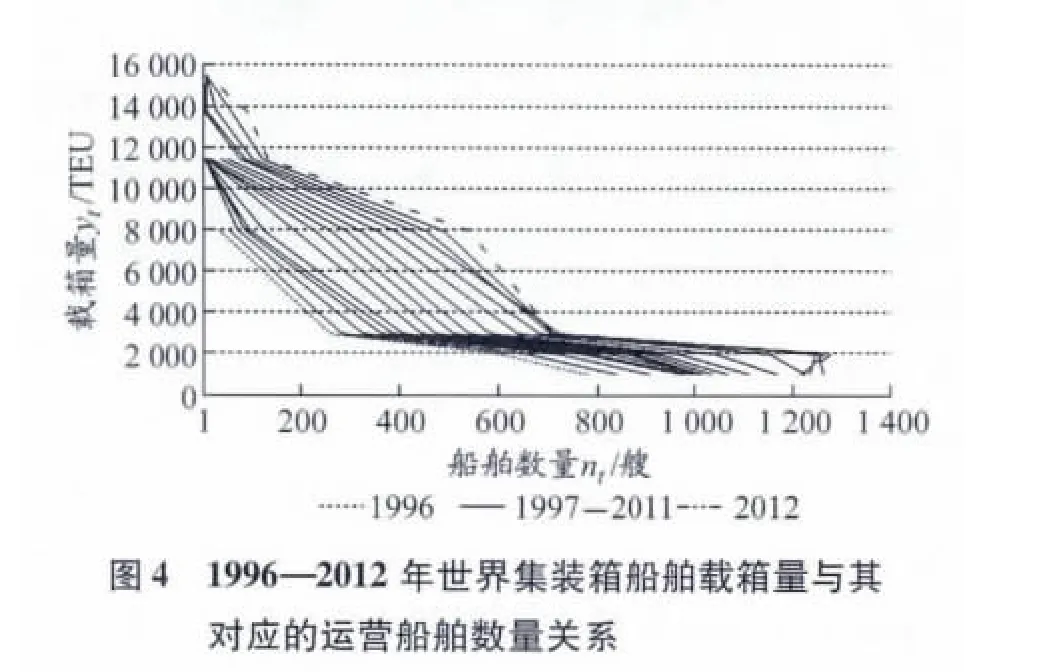
由图4可见，集装箱船舶的载箱量与其数量存在负相关性，也就是载箱量越大的船舶，其数量越少.因此，可以写出函数关系式

式中:yt为t期船舶的载箱量;nt是t期对应一定载箱量的船舶数量，且＜0.

每年的全球集装箱贸易量均由集装箱船舶完成，因此有

式中:ntmax为t期最小船型的数量;ρ为运力运量转换系数.

3 验证

显然，要求解式(3)存在一定困难，因此需要寻找简化的方法.

3.1 模型简化

由于船舶大型化不仅考虑单船载箱量，还与特定船型的投入数量有关.考察图4，式(2)所对应的曲线族的斜率在yt≈3000 TEU时出现较大改变，这使式(2)的函数关系不易被很快发现.但是，从当前全球航线运营的船舶载箱量分布看，能够成为最大型船舶替代者的只可能是载箱量在3600 TEU以上的船舶.考虑到本文的研究内容，可以不考虑载箱量为3000 TEU以下船舶的情况.而图4中，当载箱量为3000 TEU以上时，各年度的对应载箱量与船舶数量之间的关系几乎为一直线，因此可以假定yt与nt的关系为线性函数，即存在

式中:at为计算年度曲线的斜率(at＜0);bt为计算年度船舶载箱量的截距;c+－为预测集装箱船舶最大载箱量与当年实际最大载箱量之差，取绝对值.模型分析流程见图5.

图5 模型分析流程

将图4中的数据按年度分别代入式(4)进行线性回归计算，结果见表2.

表2 图4中各曲线线性回归数据

由表2可知:计算期内各年的船型和数量方程与实际数据的拟合度均满足合理性要求，R2最小的也为0.932;但是at和bt均不为常数，具体而言就是这些曲线相互间不平行，且间距也不固定，但都可以获得船舶载箱量与船舶数量曲线，见图6.

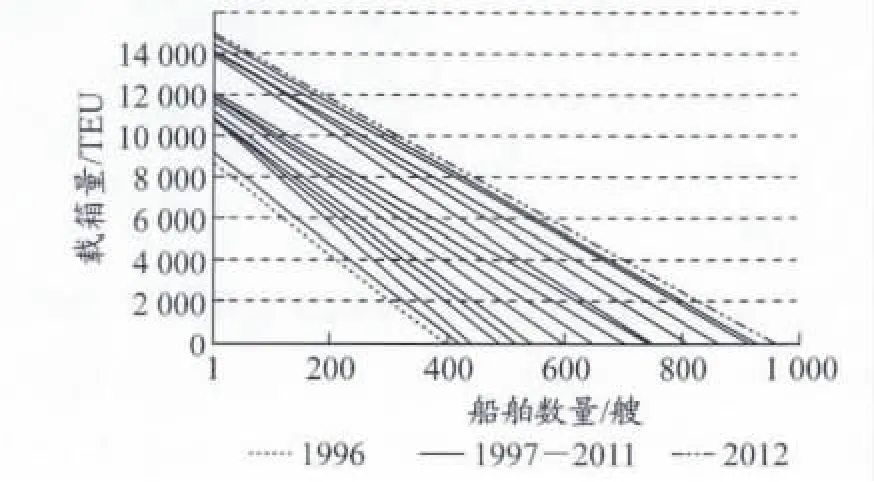
图6 1996—2012年船舶载箱量与船舶数量线性趋势线分布

3.2 试算

这里尝试用时间序列求出at和bt的变化规律.

3.2.1 计算 at

先作出at的时间序列散点图，见图7.通过线性回归，可以得出at的计算式

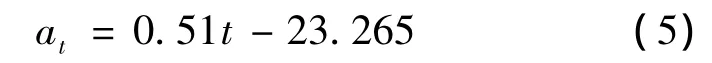
式(5)的R2=0.8329＞0.75，可以认为其符合线性规律.

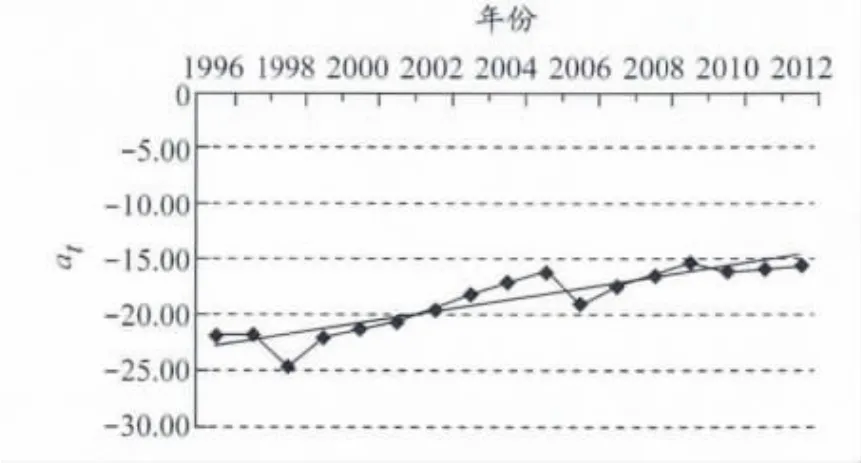
图7 1996—2012年趋势线斜率

3.2.2 计算 bt

先作出bt的时间序列散点图，见图8.通过线性回归，可以得出bt的计算公式

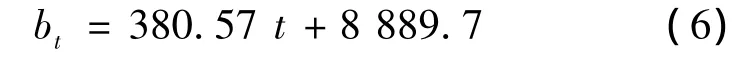
式(6)的 R2=0.9459＞0.75，可以认为其符合线性规律.

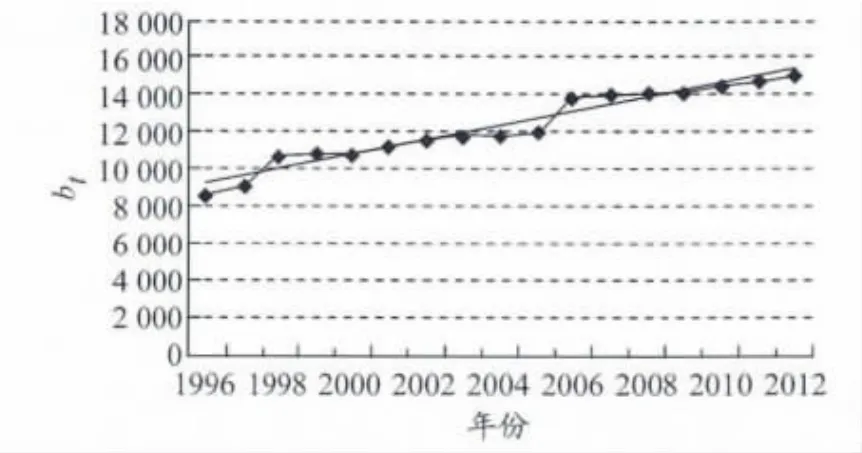
图8 1996—2012年趋势线截距

3.3 误差求取

3.4 预测

根据式(5)和(6)，可以分别求出预测年份的at和bt，代入式(4)即构成预测年份的载箱量与船舶数量关系函数.在本例中，可以预测出2020，2025和2030年载箱量与船舶数量关系函数，分别见式(8)，(9)和(10).

从2020年到2030年各主要预测年份的载箱量与船舶数量关系曲线见图9.在式(10)中，当n30取值为最小值1时，y30取值为

4 结束语

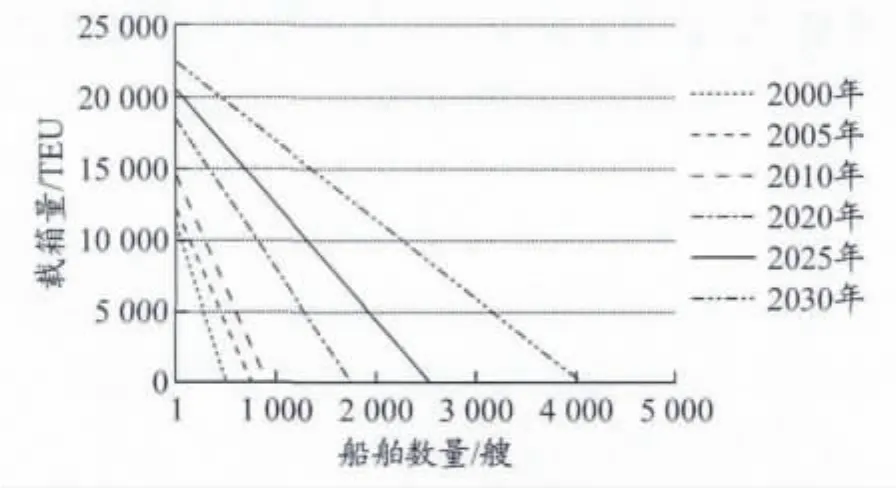
图9 2020，2025和2030年集装箱船型发展趋势预测

采用图形分析与时间序列回归相结合的方法，给出集装箱船舶最大载箱量的算法.根据这一算法，可以较为准确地估计出未来年份将出现的最大集装箱船舶载箱量.这对船舶设计部门、建造部门以及港口企业无疑是十分重要的.本文没有考虑航道、码头等对船舶大型化的限制，主要是因为此类大型船舶多数安排在大洋航线上.当然，影响集装箱船舶大型化的因素很多，如港口设施［13－14］、国际经济走向、经济一体化［15］、船舶技术和世界航运格局等.

本算法仅仅是在集装箱船型领域的一项探索，其计算精度也需要采用更为合理的算法加以提高.希望这种思路也可以用于干散货、油船等其他类型船舶的最大载货量预测上.

［1］郑楼先，林晓东.集装箱船舶大型化的利与弊［J］.船海工程，2005(4):79－80.

［2］陈飞儿，张仁颐.基于水运系统的超大型集装箱船经济可行性论证［J］.船舶工程，2008，30(1):78－81.

［3］赵一飞.论集装箱船的大型化趋势［J］.上海造船，1995(3):1－7.

［4］IMAI A，NISHIMURA E，PAPADIMITRIOU S，et al.The economic viability of container mega－ships［J］.Logistics ＆ Transportation Rev，1997，21(4):32－34.

［5］CULLINANE K，KHANNA M.Economies of scale in large container ships［J］.J Transport Econ ＆ Policy，2000，33(2):185－207.

［6］CULLINANE K，KHANNA M.Economies of scale in large containerships:optimal size and geographical implications［J］.J Transport Geography，2000，8(3):181－195.

［7］仇鑫尧.中远集团建造超大型集装箱船技术经济可行性分析［D］.上海:上海海运学院，2003:37－41.

［8］吴冲.集装箱船舶大型化规模经济研究［D］.上海:上海海事大学，2005.

［9］张仁颐.水运物流系统分析［M］.上海:上海交通大学出版社，2007:87－88.

［10］BRANCH A，STOPFORD M.Maritime economics［M］.3rd ed.Oxon:Routledge，2009:45－47.

［11］CLARKSONS.Container intelligence quarterly［R］.Third quarter 2012:13.

［12］陈丽江，苏含秋.中国国际集装箱班轮运输市场运价趋势分析［J］.上海海事大学学报，2005，26(4):75－76.

［13］高洁.上海港集装箱运输竞争力评价［J］.上海海事大学学报，2005，26(4):67－72.

［14］曹金虎，薛士龙，陈加敏，等.基于PLC和组态王的高效自动化集装箱码头监控系统设计［J］.上海海事大学学报，2011，32(2):25－28.

［15］郭永红.集装箱船大型化经济性分析［D］.大连:大连海事大学，2000.