基于ARCH族模型的中国出口集装箱运价指数波动特征

朱玉华，赵刚

(上海海事大学交通运输学院，上海 201306)

0 引言

中国出口集装箱运价指数(China Containerized Freight Index，CCFI)是全球唯一的集装箱运价指数，目前已成为反映我国集装箱航运市场状况的重要指标.研究CCFI的波动规律，可为企业和政府掌握集装箱运输市场变化规律提供重要的决策依据.

目前，国内外学者主要针对波罗的海干散货运价指数的波动性进行研究，对集装箱运价指数的波动研究较少.VEENSTRA等［1］应用向量自回归(Vector Auto－Regressive，VAR)模型对干散货运价指数进行分析;宫进［2］对波罗的海运价指数收益率的季节效应进行研究;李序颖等［3］对我国交通货物运输量进行时间序列分析;王军等［4］利用广义自回归条件异方差(Generalized Auto－Regressive Conditional Heteroskedasticity，GARCH)等模型研究世界原油运价的波动特征;陆克从［5］利用自回归条件异方差(Auto－Regressive Conditional Heteroskedasticity，ARCH)模型研究波罗的海好望角型船运价指数波动情况;张页［6］运用协整理论研究CCFI与相应航线运价的相关性;刘翠莲等［7］利用ARCH族模型对我国沿海煤炭运价指数的波动性进行研究;林国龙等［8］应用CF滤波方法研究干散货航运市场的周期性趋势.关于ARCH族模型的研究，WEIGEND等［9］于1993 年首次提出自回归(Auto－Regressive，AR)模型;ENGLE［10］应用ARCH模型研究通货膨胀率建模问 题;BOLLERSLEV 提 出 GARCH 模 型［11］和TARCH 模 型［12］;在 TARCH 模 型 的 基 础 上，NELSON［13］提出指数 GARCH(EGARCH)模型;DING 等［14］提出 ARCH(APARCH)偏幂模型.本文重点利用ARCH族模型研究CCFI的波动规律，包括CCFI收益率序列的平稳性、异方差性和波动特征，为提高我国出口集装箱运输市场预测的可靠性提供重要参考.

1 基于ARCH族模型的序列波动性研究方法

1.1 ARCH 模型

ENGLE于1982年引入条件方差的概念分析方差变化的原因，并提出ARCH模型，指出金融时间序列{yt}的条件方差{ht}会随时间变化，因而可视{ ht}为条件均值方程随机误差项{μt}滞后项的函数，即收益率波动取决于以往的消息.AR(p)－ARCH(q)模型表示为

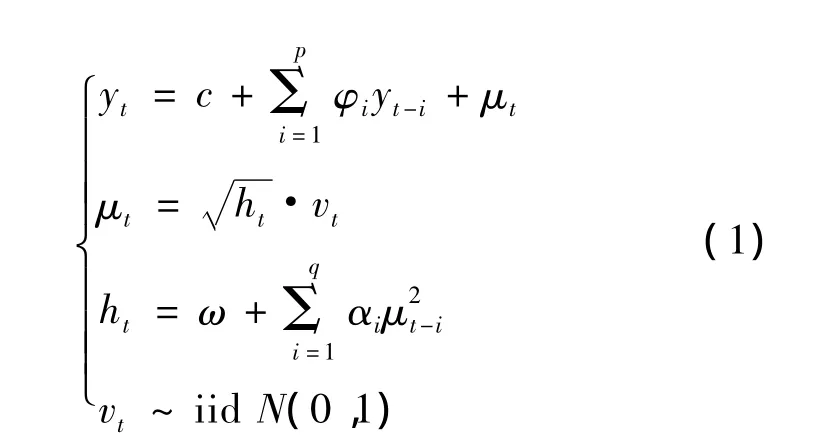
式中:α1，α2，…，αq，ω 为待估参数;{μt}服从q阶的ARCH过程.由式(1)可知:对i期预期收益的变动对当期波动度的影响由αi决定，q值反映μt的某一波动情况持续的时间，因此该模型能够反映市场的波动聚集性.

1.2 GARCH 模型

GARCH(p，q)模型基本表达式为

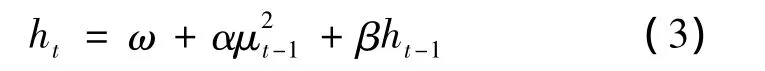
式中:α反映前一期的波动情况，其大小反映市场变化引起的序列波动性大小;β大小反映前一期的波动对序列影响的持续时间长短.虽然GARCH模型能够解决高阶ARCH模型的拟合问题，但不能反映时间序列波动的非对称效应(即杠杆效应).

1.3 EGARCH 模型

EGARCH模型可以反映波动度对好、坏消息的非对称影响，用方程表示为

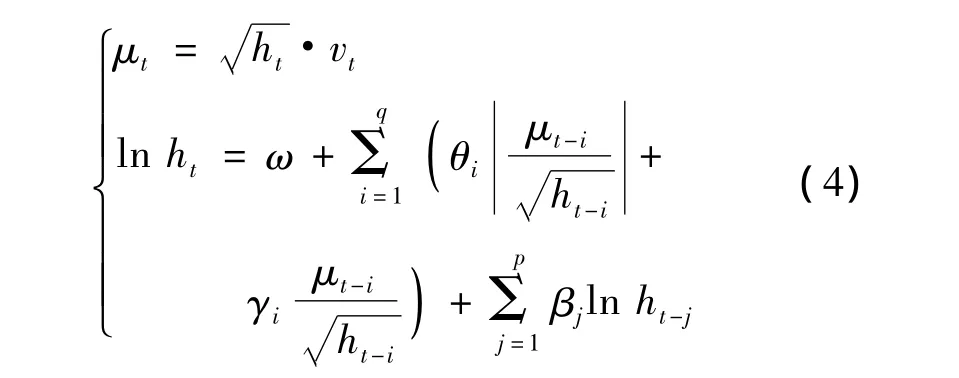
2 数据的选取及实证研究

2.1 数据的选取与处理

选取上海航运交易所发布的CCFI，样本区间为2000年1月7日至2012年8月31日的周数据，共得到586个观测值，利用EViews 6.0对相关数据进行处理.CCFI走势见图1.

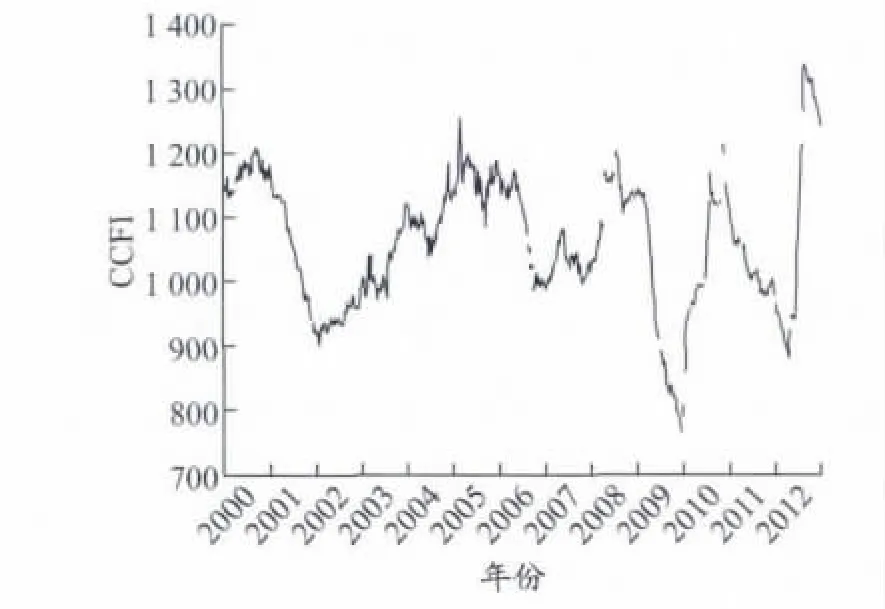
图1 CCFI走势

从图1中可以看出，CCFI周数据波动幅度比较大，且呈不规则的锯齿状波动，最高点(1335点)与最低点(763点)相差近1倍，尤其是2008年以来CCFI经历两次前所未有的大振幅.为了研究CCFI收益率的波动情况，本文以CCFI相邻周的价格指数对数的1阶差分作为CCFI的收益率.设差分后的CCFI收益率为RCCFIt，t时刻CCFI价格指数为ICCFIt，则 RCCFIt=ln ICCFIt－ ln ICCFIt－1，从而得到 CCFI收益率序列{RCCFI}，见图2.

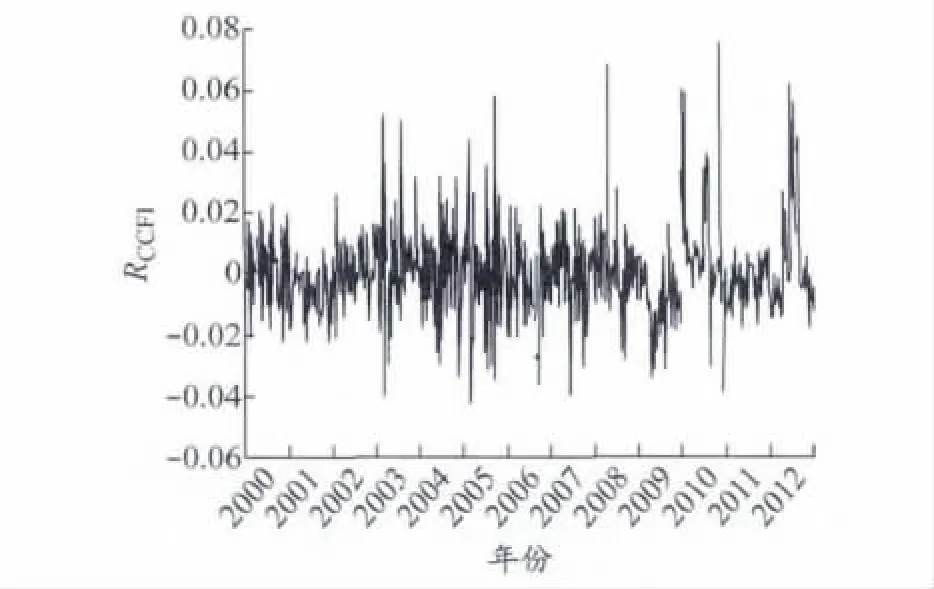
图2 CCFI收益率序列

2.2 CCFI收益率序列的基本统计特征

应用EViews 6.0可以得到{RCCFI}的基本统计特征，见表1.

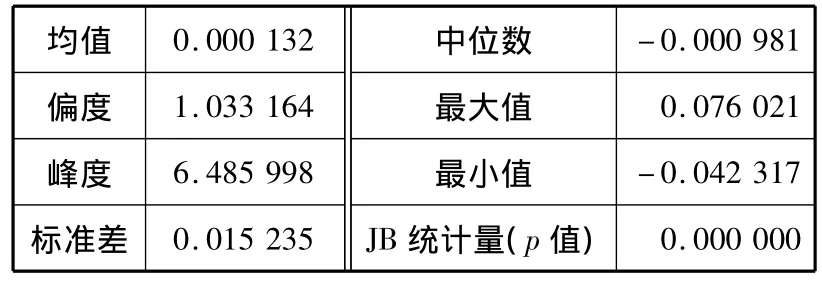
表1 {RCCFI}序列的基本统计特征

由表1可见，{RCCFI}具有以下特征:(1)收益率序列具有波动集群的特征;(2)收益率的均值为正值，表明在样本区间内集装箱运输业总体平均收益为盈利;(3)偏度系数大于0，表明收益率序列的非对称性，且为右偏;(4)峰度系数大于3，表明收益率序列的尖峰厚尾特征;(5)JB统计量的尾概率为0，表明收益率序列拒绝正态分布的原假设.

2.3 CCFI收益率序列的平稳性检验

对{RCCFI}采用 Augmented Dickey－Fuller(ADF)单位根检验，结果见表2.

表2 {RCCFI}序列ADF检验结果

从检验结果看，单位根检验的Mackinnon临界值分别为 －3.441357，－2.866287，－2.569358，t统计量为－10.376820，均小于相应的临界值，从而拒绝原假设，表明{RCCFI}不存在单位根，是平稳序列.

2.4 均值模型确定和残差序列的ARCH效应分析

利用LBQ(Ljung－Box Q)法对{RCCFI}进行自相关性检验，结果见表3.

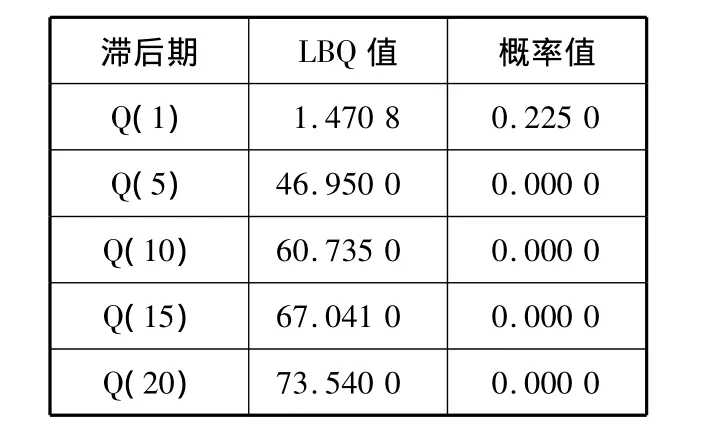
表3 CCFI收益率序列的LBQ检验

由表3可知，随着滞后期的增加，LBQ对应的相伴概率都近似为0，由此拒绝各收益率序列不存在自相关性的假设，认为{RCCFI}存在自相关.通过对CCFI收益率序列自相关函数及偏自相关函数截尾性和拖尾性的考察，可以判定自回归和移动平均的阶数，进而确定拟合模型的基本形式.用EViews 6.0分别计算{RCCFI}的偏自相关、自相关系数，发现{RCCFI}的偏自相关函数表现为3步截尾，而自相关系数表现为拖尾，由此判定{RCCFI}为AR(3)过程.建立序列{RCCFI}的AR(3)模型如下:

为检验拟合方程的残差序列是否具有异方差性，对{RCCFI}用普通最小二乘法估计，所得各项系数见表4.

表4 拟合方程系数

由表4可知，AR(1)的系数β1没有显著性，说明 RCCFIt－1对 RCCFIt的贡献度不显著.剔除AR(1)项后重新拟合均值方程，结果见表5.

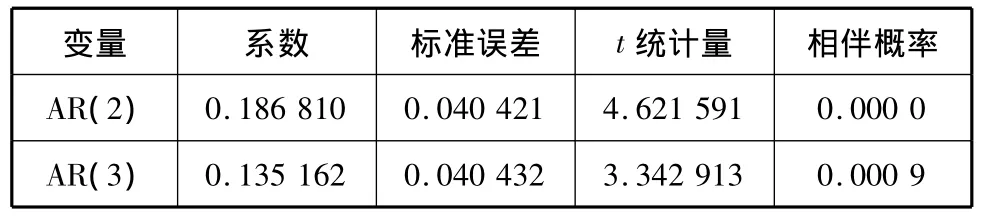
表5 重新拟合方程系数

由表5可知，方程各项系数都已通过显著性检验，可以得到拟合方程

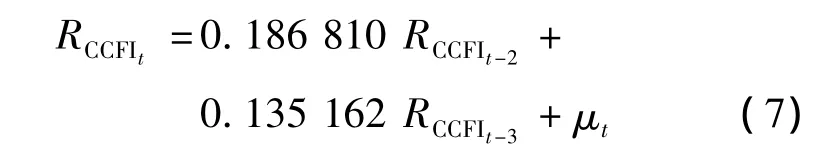
R2=0.056，对数似然值 =1625.063，AIC值 =－5.577537，SC 值= －5.562532.

{RCCFI}回归方程的残差见图3.从图3中可发现，序列具有波动集聚效应，可以判断CCFI具有异方差性.对{RCCFI}回归方程的残差项序列进行ARCH效应检验，结果见表6.

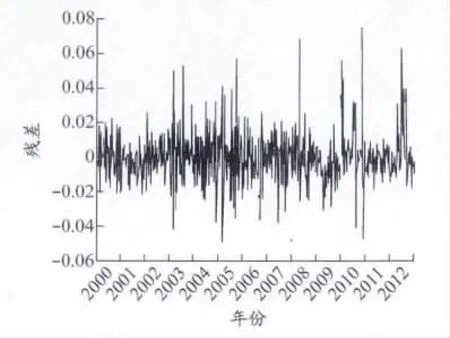
图3 {RCCFI}回归方程的残差

表6 {RCCFI}回归方程的残差项序列的ARCH效应检验结果

由表6可知，{RCCFI}残差序列的各检验统计量的相伴概率全都小于5%的临界值，表明该序列具有高阶的ARCH效应.

2.5 CCFI的GARCH分析

由于{RCCFI}序列回归方程的残差项具有异方差性，且具有高阶ARCH效应，用ARCH模型对序列进行拟合需设定较大的滞后阶数，因此可用GARCH模型替代原来的ARCH模型.运用AIC和SC准则确定GARCH的阶数，结果见表7.

表7 {RCCFI}序列的GARCH分析

由表7可知，GARCH(3，3)模型的AIC值最小，GARCH(1，1)模型的 SC值最小.由于 GARCH(1，1)形式精简，且数据处理后发现实际得到的效果与GARCH(3，3)模型相近，因此本文用 GARCH(1，1)模型进行建模并深入分析CCFI波动的特征.构建模型结构如下:

通过拟合，整理得到CCFI收益率序列的均值方程和方差方程

各参数值及具体数据见表8.

表8 GARCH(1，1)参数估计结果

R2=0.054720，对数似然值 =1651.028，AIC值=－5.656454，SC值=－5.618941.在条件方差方程中，参数估计的Z统计量非常显著，其相应的概率值也非常小，说明这些参数估计都是显著的，而且这些参数值都大于0，满足条件方程非负要求.ARCH项和GARCH项的系数估计值之和α+β=0.631667 ＜1，证明 GARCH(1，1)为平稳过程，满足参数约束条件;对数似然值有所增加，AIC值和SC值均变小，说明GARCH(1，1)模型可很好地拟合CCFI收益率序列.

2.6 我国集装箱运输市场的波动特征分析

对CCFI收益率序列建立GARCH模型后，为了更好地分析CCFI的时变特征，可以获得对应的条件方差时序图，见图4.

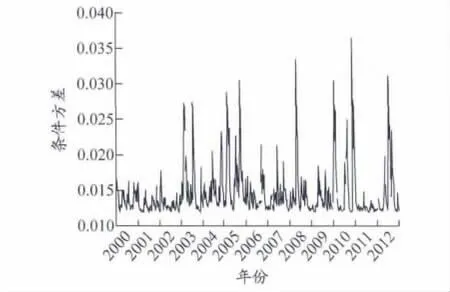
图4 {RCCFI}序列条件方差时序

从图4可见，条件方差存在极端值现象，即条件方差在某时刻附近的涨跌幅度都很大，短期内出现暴涨暴跌的情况.从条件方差序列的对比可以看出，序列涨跌的极值主要集中在5个区段，对应的时间分别是2003年1月至2003年6月，2004年9月至2005年3月，2007年9月至2008年3月，2009年12月至2010年6月，2012年1月至2012年6月.通过回顾当期CCFI，可以发现导致异常波动的原因.

(1)2003年1月至2003年6月.2003年初，亚洲地区发生非典疫情，受其影响，我国的对外进出口贸易受到较大冲击.我国集装箱出口主要有纺织服装、轻工艺产品、日用品等，非典发生后，相关贸易企业在组织货源上受阻，导致商品出口供应链脱节.非典期间，各地都强化对人员进出的控制，直接影响企业员工的招收和企业的生产.另外，国际社会也对我国进出口货物加大检验检疫力度，使得我国的集装箱进出口贸易受到一定的影响.

(2)2004年9月至2005年3月.2004年国际经济环境较好，我国经济继续保持快速增长势头，增速达9.7%左右，这是我国经济自1997年以来同期的最高增速.经济快速增长带来对交通的旺盛需求，集装箱吞吐量呈现出大幅增长的良好态势.这一时期，全球集装箱运输市场包括太平洋航线、亚欧航线和大西洋航线等3大主干航线市场货量需求旺盛，船公司舱位利用率总体较高，运价也在年初基础上有一定幅度的上涨，给承运人带来丰厚的收益.

(3)2007年9月至2008年3月.2007年2月，美国爆发次贷危机，并逐渐演变成全球金融危机，之后迅速向金融领域以外的其他实体经济传播，最终升级为全球经济危机.经济危机导致市场流动性严重短缺，投资和消费信心受挫，我国出口产品增长放缓，货量下滑，舱位利用率降低，国际集装箱运输市场进出口箱量与往年相比明显减少.另外，金融危机导致美元贬值，触发国际原油价格飙升，并直接或间接地刺激各种商品和原材料的交易价格上涨，且美元贬值直接促使人民币升值，导致我国出口贸易的价格竞争力进一步降低，对我国出口集装箱运输需求下降.

(4)2009年12月至2010年6月.2003年以来，世界经济进入快速发展时期，我国的经济贸易也一直保持繁荣和发展;受世界经济和我国经济贸易快速发展、市场需求旺盛的刺激，我国的集装箱进出口业务进入高速发展的繁荣期.2008年国际金融危机给世界经济造成巨大影响，我国的集装箱进出口业务量也开始大幅萎缩.危机发生以后，各国采取一系列促进经济增长的措施，经过一年多的努力，2009年12月至2010年6月间集装箱进出口贸易量有一定回升，主要航线的运价也得到一定上涨.

(5)2012年1月至2012年6月.2012年初，国际集装箱运输市场并未像干散货和油运市场一样低迷，在许多国家节后逐步恢复开工和货主提前出货等因素的影响下，集装箱货量呈现逐步回暖态势.航运公司的平均舱位利用率从年初的70%左右上升到一季度末的90%左右.主要航线运价触底反弹，运价上涨幅度明显，其中欧洲航线上涨幅度较大，平均上涨约700美元/TEU.二季度，受美国经济复苏和旺季效应影响，货量基本保持稳定，航线运价和运量都稳步增长.

从以上分析可知，集装箱班轮运价受世界宏观经济波动、运输市场需求供给、国际贸易等因素影响较大.这是因为集装箱班轮运输需求是国际贸易的派生需求:当国际贸易繁荣、货源充足时，班轮运价就升高;反之，运价就降低.集装箱运价结构主要包括集装箱运输成本、税金和利润，在这些因素中运输成本所占比重最大，它主要受国际油价、港口费用等影响，是引起集装箱运价长期变化的原因.集装箱运价短期巨幅波动主要是受世界宏观经济波动、运输市场的需求供给和国际贸易状况变化等因素所引起的.

2.7 CCFI波动的非对称性分析

为了反映集装箱运输市场的非对称性，在上文GARCH(1，1)的基础上选用EGARCH模型对CCFI收益率序列表现出的波动性进行分析.EGARCH(1，1)模型建立如下:

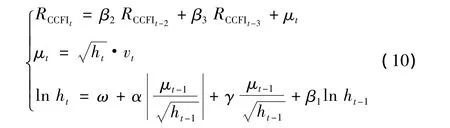
通过拟合，整理得到CCFI收益率序列的均值方程和方差方程

R2=0.053448，对数似然值 =1649.896，AIC值=－5.649126，SC值=－5.604110.从以上数据可以发现，γ=0.104221＞0，说明CCFI收益率序列具有杠杆效应，且对市场“利好”消息的敏感程度大于“利空”消息.当集装箱运输市场出现“利好”消息时，杠杆效应参数α+γ=0.253023+0.104221=0.357244，即“利好”消息会给收益率条件方差带来0.357244倍的冲击;当集装箱运输市场出现“利空”消息时，杠杆效应参数 α－γ=0.253023－0.104221=0.148802，即“利空”消息会给收益率条件方差带来0.148802倍的冲击.对于我国出口集装箱运价市场而言，“利好”消息比等量的“利空”消息产生的冲击更大，具有反杠杆效应.

由于国际集装箱班轮运输业是资本密集型、技术密集型行业，班轮运输企业进入和退出的门槛较高，集装箱班轮运输市场具有寡头垄断的市场结构特征.因此，在该市场中集装箱班轮运输价格主要由较大的班轮公司或者联盟主导，规模较小的航运公司一般只能采取从价策略，当“利好”消息出现时，起主导地位的大型班轮公司或者联盟会迅速作出反应，推高班轮运价以获得最大利润;当“利空”消息出现时，他们则常常采取措施抵制市场不利因素带来的冲击，减缓运价下跌的速度，减少运输损失，由此导致集装箱运价市场的反杠杆效应.

3 结论

综合运用ARCH族模型对我国出口集装箱运输市场的波动性进行评价分析，主要结论如下:

(1)CCFI收益率序列的基本统计特征表明该序列不服从正态分布，具有金融时间序列的尖峰厚尾和集聚性特征，且具有异方差性，市场波动性大.

(2)GARCH(1，1)模型能够较好地拟合CCFI的波动特征，能够反映CCFI的敏感性和持续性.CCFI受外部冲击敏感度较强，冲击作用效果持续时间长.集装箱运输企业在面临运价波动风险时，不能被动应付集装箱运价波动的影响，在正确把握集装箱运价走势和波动的基础上，应该积极利用我国正在培育和发展的航运衍生品市场，主动进行集装箱运价的衍生品交易，对集装箱运价波动风险进行有效管理和控制.

(3)EGARCH(1，1)模型能较好地捕捉“利好”“利空”消息对我国集装箱运输市场价格变化的反映程度，指出我国出口集装箱运输市场波动具有非对称效应，市场对“利好”消息比较敏感，表现为反杠杆效应，这主要是由集装箱运输市场的寡头垄断结构特点决定的.集装箱班轮运输企业需要准确及时地掌握集装箱运输市场信息，分析市场变化趋势，根据集装箱运价的波动情况，把握时机、及时调整本企业的运力或者优化航线网络结构，提高对集装箱运输市场的驾驭能力.

［1］VEENSTRA A W，FRANSES P H.A co－integration approach to forecasting freight rates in the dry bulk shipping sector［J］.Transportation Res，1997，31(6):447－458.

［2］宫进.国际干散货运价风险相关问题的实证研究［D］.上海:上海海事大学，2001.

［3］李序颖，岳丹，顾岚.我国交通货物运输量的时间分析［J］.系统工程理论与实践，2005，25(1):49－51.

［4］王军，张丽娜.基于广义自回归条件异方差模型的世界原油运价风险分析［J］.上海海事大学学报，2011，32(2):20－24.

［5］陆克从.波罗的海好望角型船运价指数波动分析［J］.上海海事大学学报，2008，29(4):29－33.

［6］张页.中国出口集装箱运价指数与实际运价相关分析［J］.中国航海，2010，33(2):96－100.

［7］刘翠莲，刘健美，杨娟，等.基于ARCH模型的沿海煤炭运价指数波动性评价［J］.武汉理工大学学报:交通科学与工程版，2012，36(3):445－449.

［8］林国龙，陈言诚.基于CF滤波的国际干散货航运市场周期性分析［J］.上海海事大学学报，2012，33(3):69－74.

［9］WEIGEND A S，GERSHENFELD N A.Time series prediction:forecasting the future and understanding the past［M］//Reading，MA:Addison－Welsley，1993.

［10］ENGLE R F.Autoregressive conditional heteroskedasticity with estimate of the variance of United Kingdom inflation［J］.Econometrica，1982，50:987－1007.

［11］BOLLERSLEV T.Generalized autoregression conditional heteroskedasticity［J］.J Econometrics，1986，31:307－327.

［12］BOLLERSLEV T.Conditionally heteroskedastic time series model for speculative prices and rates of return［J］.Rev Econ ＆ Stat，1987，69:542－547.

［13］NELSON D B.Conditional heteroskedasticity in asset returns:a new approach［J］.Econometrica，1991，59:347－370.

［14］DING Z，GRANGER C W J，ENGLE R F.A long memory property of stock market returns and a new model［J］.J Empirical Finance，1993(1):83－106.