用阶梯变化金属纳米光栅增加介质中的光吸收

中国科学院半导体研究所 集成光电子学国家重点实验室 于丽娟 左玉华 郑军

一 引言

等离子体光子学(Plasmonics)的出现为陷光技术的发展注入了新的活力。纳米金属结构产生的表面等离子体激元(Surface Plasmon Polariton，SPP)[1]是由光和金属表面自由电子的相互作用引起的一种电磁波模式。它局限于金属与介质界面附近，并沿表面传播。通过选择合适的纳米金属结构，能够将光聚集或是“折叠”到半导体薄膜吸收层内，进而提高薄膜材料的吸收能力。由于等离子体可以将光波聚集到深亚波长体积上，能够很好地突破衍射极限，在纳米光子技术中可用于高速光探测器[2]、光调制器、生物传感器[3]、激光器、突破衍射极限的成像等各类有源或无源光电子器件。

我们都知道，在光伏电池的实际应用中器件对光谱的吸收响应越宽越好，这是因为光伏器件本身就是广谱响应器件。但传统设计的SPs 结构通常只能激发频谱上较窄的共振，意味着由激发传统SPs 所带来的吸收增强也无法覆盖较宽的频谱范围。在薄膜太阳电池的研究中，提高薄膜太阳电池的效率一直是人们关注的热点之一[4]，太阳能具有宽广的光谱，通常情况下，光能不能被单结Si薄膜电池完全吸收，特别是波长大于1000nm的太阳光，为了充分利用波长在1200nm、1600nm附近的太阳光，本文设计了一种周期变化的金属光栅来增加这3个波段光吸收。本文用FDTD方法，通过对一维金属光栅透射特性的模拟计算和分析，证明了这种金属结构可以增强介质内的光场强度。为了简化分析计算，本文采用SiO2介质和金属Ag光栅材料进行数值模拟。

二 光栅SPs理论

金属与介质界面能够产生表面等离子波，从色散关系看[1]，用光激发SPs问题在于表面等离子体波矢ksp＞ω/c，给定光子能量h ω的波矢h ω/c必须增加一个Ækx，所以局域表面等离子的共振频率除了与金属和介质的材料有关之外，还与微结构的尺寸形状有关。要实现入射光波与表面等离子体的耦合，必须通过波矢补偿达到动量匹配，而通过一维纳米光栅的方法可以实现波矢匹配[5]。通常金属与不同介质界面产生的SPs的波矢可以简单表示为:

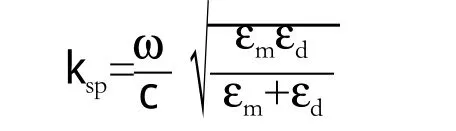
其中:ksp为SPs波矢，ω为角频率，c为光速，εm为金属介电系数，εd为介质介电系数。

本文的模拟分析中，为方便介质材料选SiO2，另外，薄膜太阳电池也常常用SiO2做增透膜。金属材料选择Ag，因为金属Ag纳米结构在近红外光波段具有较强的增透特性。FDTD方法模拟求解时，所使用的所有复介电常数值来源于国际上被广泛应用的实际测量值[6～8]，并用Drude-Lorentz模型拟合数值。

三 模拟设计

利用二维结构时域差分(finite difference time domain，FDTD)算法进行数值模拟，设SiO2(折射率为1.53)的厚度为200nm，表面用周期变化的金属银光栅，光栅宽度和周期可变。模拟区域选择一个周期的x-z平面。为了确保数值计算的准确我们设定计算网格单元为2nm×2nm，并在外围设置周期性边界条件，入射光为沿z 方向传播的p偏振平面波(Ex，Ez，Hy)，即电场分量Ex垂直于纳米金属条。由于太阳电池及光探测器的材料光跃迁速率与电场振幅的平方成正比，我们分别监测SiO2衬底中不同深度(50nm，100nm，150nm)的透射电场强度(可以代表由SPs 耦合出的电场增强)，图1所示为模拟结构示意图，入射光为z方向把Ag与SiO2的界面定为坐标原点。设定周期性边界条件，入射光为TM偏振光(Ex，Ez，Hy)电场分量Ex垂直于金属光栅。

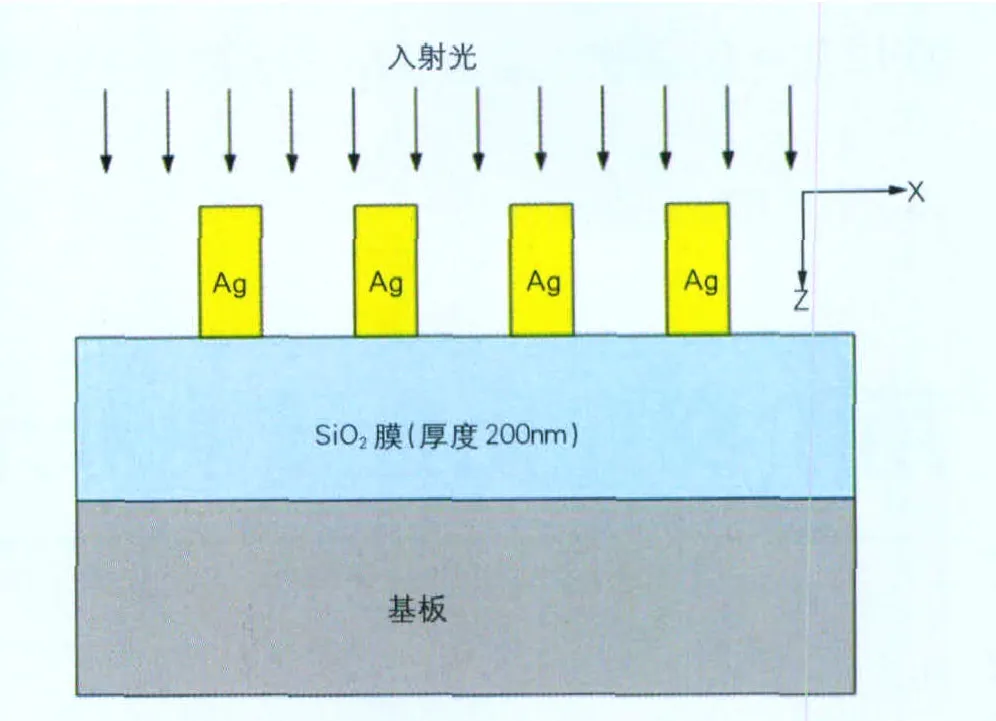
图1 模拟结构详细示意图

模拟中分别扫描了1000～1400nm、1400～1800nm两个红外波段，在相同条件下，分别对SiO2介质上有Ag光栅和没有光栅的情况下，SiO2介质中50nm处的透射电场随入射波长的变化进行模拟，并进行归一化处理，所输出的电场为归一化的。

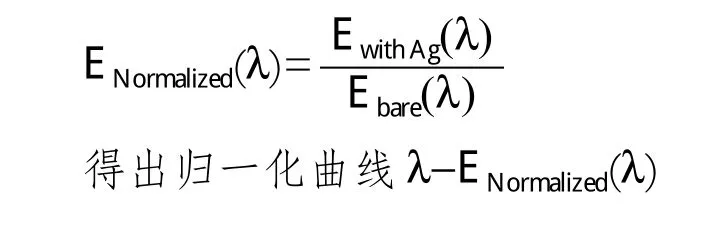
四 模拟结果与讨论

图2为宽300nm，高100nm的纳米Ag光栅，在不同周期下，介质中50nm处的归一化电场增强。从图中可以看到，在光栅宽度不变的情况下，随着周期的增加共振波长逐渐红移，而场增强呈递减趋势。周期1150nm时，透射电场最大增强7.5倍，在1200nm透射电场最大增强3倍，直至周期增至1100nm时，透射电场仍有2倍的增强。因此光栅宽300nm，高100nm，周期从1000～1100nm对介质中的电场均有增强作用，增强的峰位主要决定于光栅的周期。

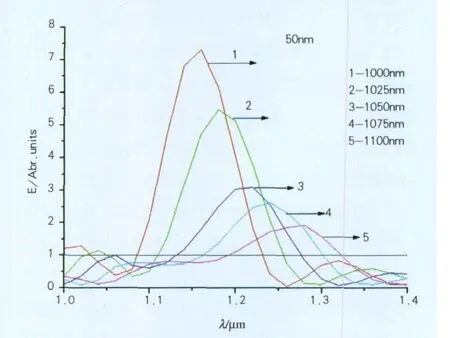
图2 纳米Ag光栅宽300nm，不同周期，介质中50nm处的归一化电场增强

因为太阳光谱红外波段的第一个小峰中心波长是1200nm，所以我们考虑对1200nm波长的增强，在周期(1025nm)不变的情况下改变纳米Ag光栅的宽度。图3为在不同光栅宽下介质中50nm处的归一化电场增强，可以看到场增强的峰位与光栅的宽度关系不大。而随着光栅宽度的增加，透射电场逐渐增加，当光栅宽从200nm增加到500nm时，透射电场最小为1倍，最高增强9.5倍。可以看出光栅越宽，透射电场越强，这与以往的预测不同。

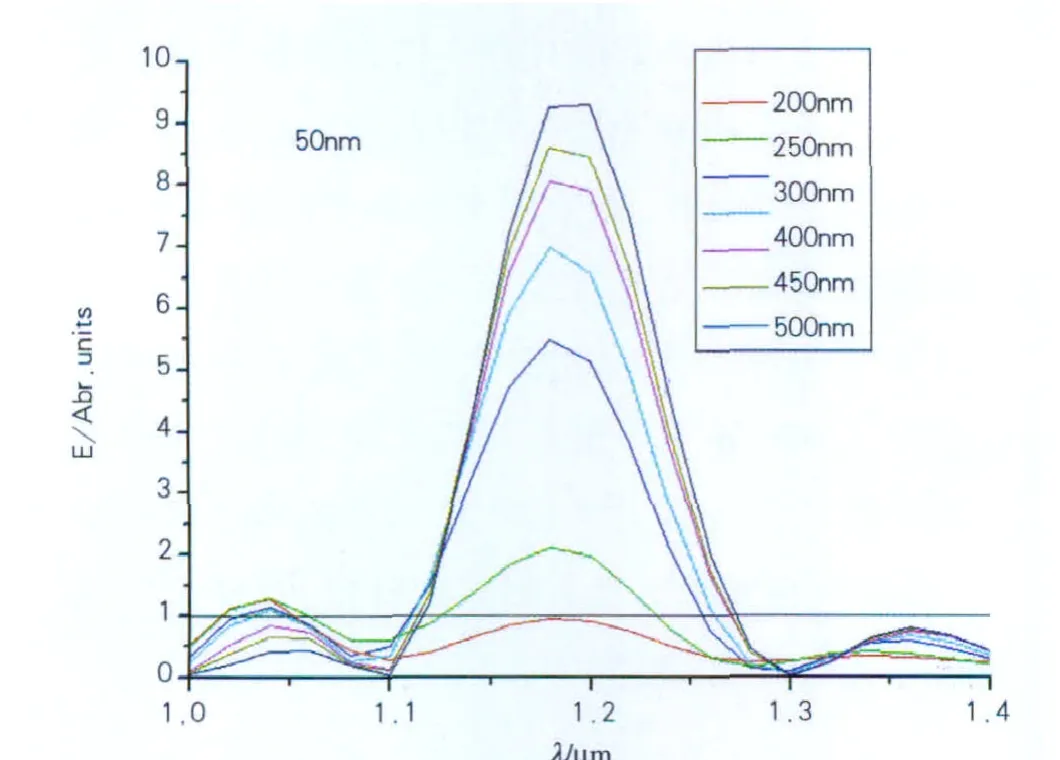
图3 纳米Ag光栅周期1025nm，不同光栅宽，介质中50nm处的归一化电场增强

图4所示为光栅宽300nm，高100nm，周期1025nm结构下，入射光波1200nm时的稳态场分布，z=0为SiO2与Ag的分界线，z从0−(-0.1)为矩形部分为金属光栅Ag, z从0−0.2µm为SiO2。从图4a可以看出，矩形银下面的两个角光场强度较大，在金属与介质的界面处有较强的电场，而且介质中的电场比金属中的要强，在介质中电场的透射深度也远大于金属。图4b可以看出，不同于电场，磁场的分布集中在金属的下边，在金属与介质的分界面处有很强的磁场分布，介质中的场大于金属中的，在界面下面显示了非常强场的透射增强和局域化作用。整个透射增强范围从500nm一直延伸至1200nm。处在波长1200nm附近的增强峰强度达到3，SiO2层内50nm处相对参考值而言有近200%的增强，随着与Ag- SiO2界面距离的增大，增强值减弱。这是由于SPs本身仅局限在Ag- SiO2界面处，而其局域增强的作用也仅作用于数百纳米的近场，这与传统超透射光栅的研究有所区别。

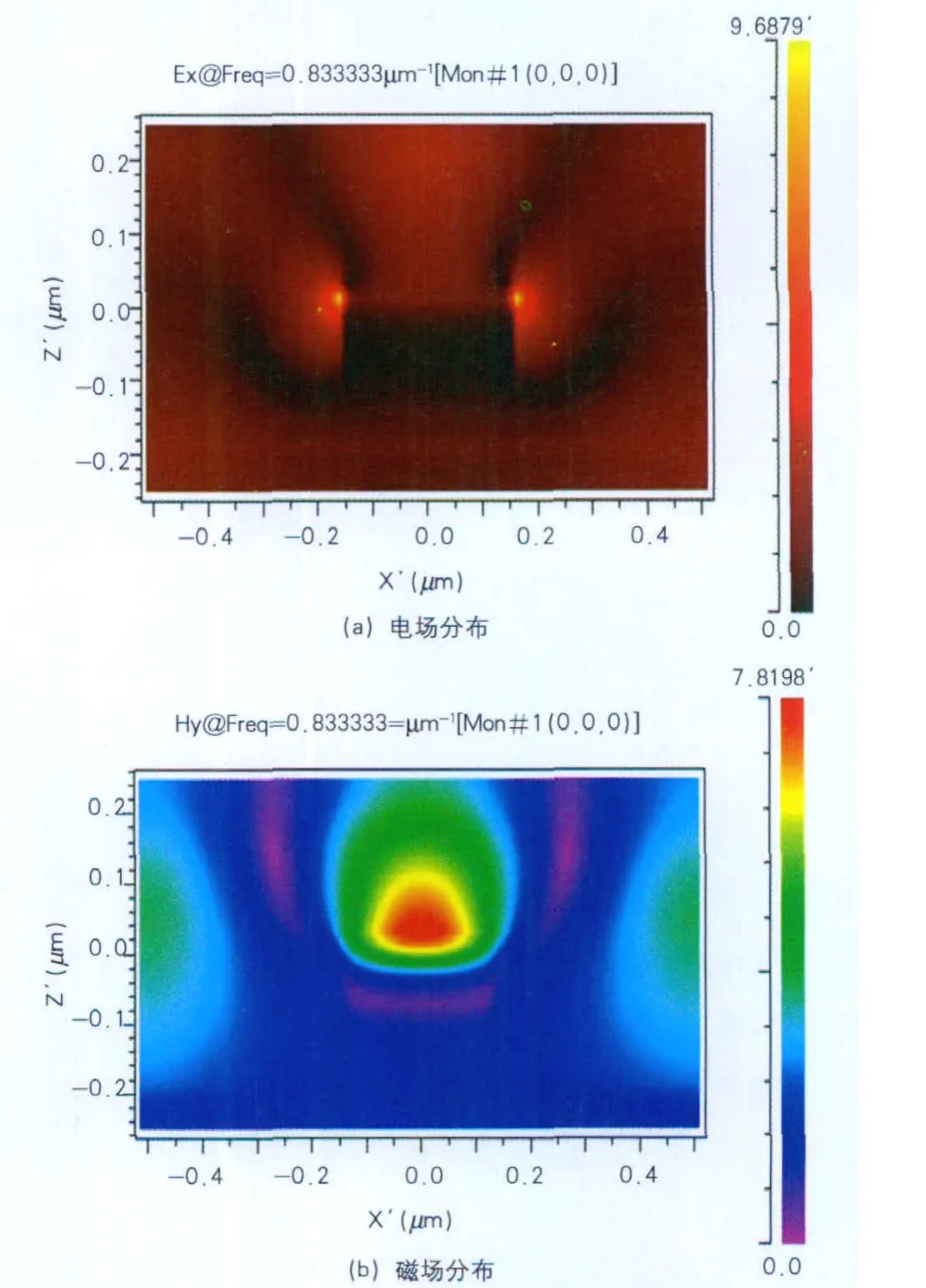
图4 Ag/SiO2波长1200nm时的z方向稳态场分布

图5为宽500nm，高100nm的Ag光栅，扫描波段1400～1800nm，在不同周期下，介质中50nm处的归一化电场增强。从图中可以看到，在光栅宽度不变的情况下，随着周期的增加共振波长逐渐红移，而场增强呈递减趋势。场增强最大在2.75，中心波长1250，而靠近或大于1600nm处并没有得到太好的模拟结果，原因可能是波长越长，波矢量越小，需要的波矢补偿较大，表面等离子体激发越难，激发的峰位越窄，难以实现，而且因为我们输出的平均电场，光栅周期越大，光栅越宽，输出平均电场结果的准确性也越差。但从太阳光谱来看，虽然红外波段第二个峰的中心在1600nm，然而波长在1400～1700nm波段的光强都还比较强，所以尽管没有得到对中心波长1600nm增强最大的光栅结构，但宽500nm，高100nm，周期大于1225nm小于1400nm的Ag光栅结构也还可以实现表面等离子体的增强作用。

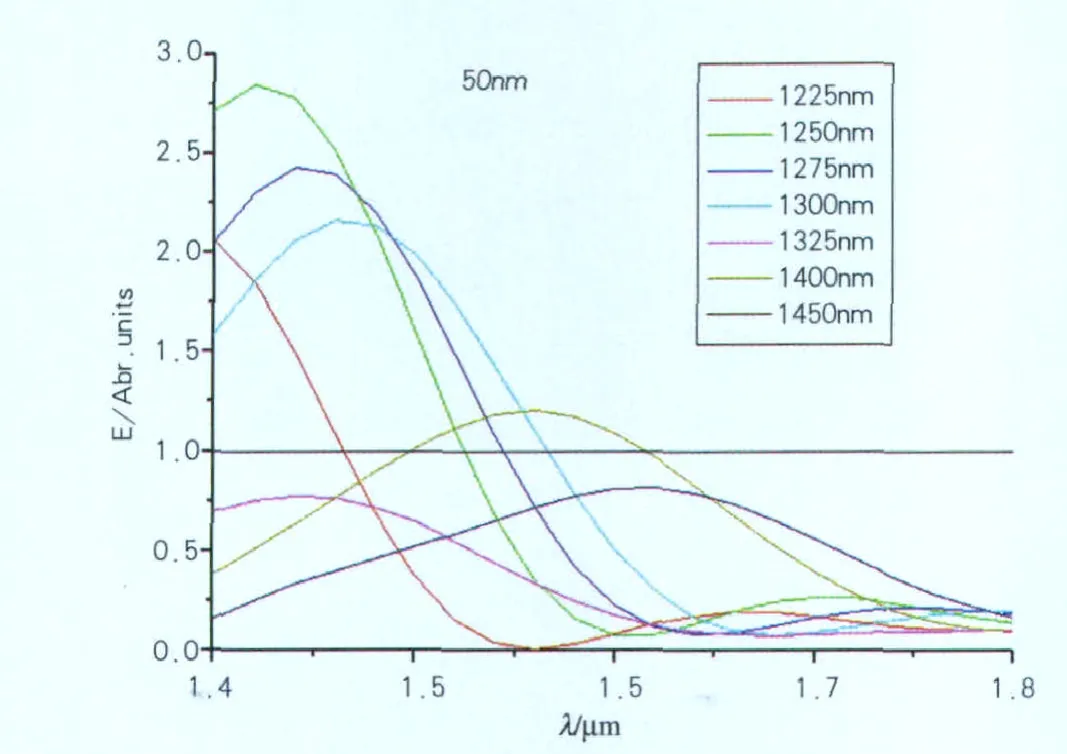
图5 纳米Ag光栅宽500nm，不同周期，介质中50nm处的归一化电场增强

图6 为宽500nm，高100nm的Ag光栅，周期1400nm，入射光波长1600nm时的稳态电场分布。光场在光栅的两端最高，原因是入射光被耦合进金属表面以SPs形式沿矩形的四个表面向两端传播，所以尖角处最强。其次在光栅与介质的接触面也有较强的电场，表现出很强的增强效应，随着离开接触面距离的增加，场强逐渐减小，在介质中的场强大于金属中的场强。

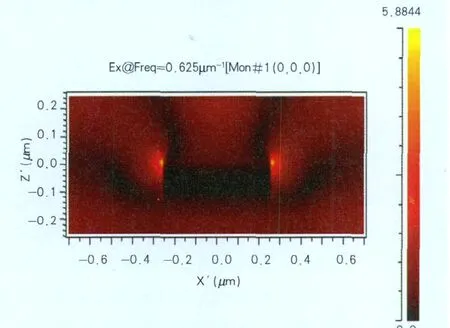
图6 Ag宽500nm，高100nm，周期1400nm，入射光波长1600nm时的稳态电场分布

五 结论

通过数值模拟得出了不同尺寸不同周期的纳米金属光栅对红外光波段1200nm和1600nm入射光的透射增强作用，通过对不同周期、不同宽的银光栅红外透射特性的模拟，分别给出了两组光栅的周期、栅高和栅宽，同时发现红外入射波长增加时，表面等离子增强较弱，对于入射波长2200nm的金属光栅只在两个角产生很强的电场，光栅底部电场很弱，所以在这里暂不考虑。因此组合两组周期不同的光栅可同时满足波长1200nm，1600nm的光波同时增强透射的功能。阶梯变化光栅式表面等离子体太阳电池结构可以拓宽吸收光谱，提高太阳电池的吸收，最大限度地将光能变成电能，从而提高了太阳电池的能量转换效率。我们模拟设计的结构可以将入射光增强并局域在百纳米的介质中，该结论对于提高薄膜太阳电池的效率具有潜在的应用价值。该设计没有考虑到金属的损耗，后续的研究将结合太阳电池材料，对金属的损耗进行进一步研究。

[1]H. Raether ,Surface Plasmons.New York, Springer-Verlag，1988

[2].L. Tang, et al. Nanometrescale germanium photodetector enhanced by a nearinfrared dipole antenna.,2008 Nature Photon. 2, 226－229

[3]J. N. Anker, et al. Biosensing with plasmonic nanosensors.2008 Nature Mater.7, 442－453

[4]Derkacs D, Lim S H, Matheu P, Mar W, Yu E T, 2006 Appl. Phys.Lett. 89093103

[5]Collin S, Pardo F,Teissier R, Pelouard J L, 2001 Phys. Rev. B 63033107

[6]E.D. Palik, Handbook of Optical Constants of Solids Vol. I,(Academic Press,Orlando, FL, 1985.)

[7]E.D. Palik, Handbook of Optical Constants of Solids Vol. II,(Academic Press,Elsevier, San Diego, CA, 1998.)

[8]E.D. Palik, Handbook of Optical Constants of Solids Vol.III,(Academic Press,Elsevier, 1998.)