气体挤压膜轴承的性能分析及其控制器的研究

朱达云 马希直

南京航空航天大学，南京，210016

0 引言

基于超声激励的气体挤压膜现象已引起国内外许多学者的关注，气体挤压膜是在压电激励条件下的一种非线性效应，主要通过高频振动不停地挤压气体，使气体产生一定的压力来克服物体的重力。目前已经研究出了各种不同的气体挤压膜机构［1-8］。1996年，Yoshiki［5］完成了弯曲波驱动下的气体挤压膜实验，证实了超声挤压膜的承载能力。Shigeka等［6］和 Stolarski等［7-8］从20世纪90年代初开始研究气体挤压膜直线导轨，致力于研究具有实际作用的线型超声挤压膜轴承。1998年吉林大学压电驱动研究室对超声挤压膜现象进行了系统的研究，初步解释了超声振动下气体挤压膜产生的原因［9］。

本文应用超声激励的气体挤压膜原理，设计了一种新型的气体挤压膜轴承。通过数值计算和有限元法分析计算了气膜的厚度、气膜压力分布、轴承的振动模态和应力分布等，并为该轴承设计了一套控制器，在实验中取得了较好的效果。

1 气体挤压膜轴承的结构和工作原理

本文提出的气体轴承的结构如图1所示，这个系统包括一个基于弹性铰链的滑块，一个直线导轨及压电驱动陶瓷。轴承实物如图2所示。

图3是该滑动轴承的剖视图。由于该轴承是轴对称结构，所以在对其进行分析时，可取其一部分进行研究。单元A是提供高频振荡的部分，单元B是用来和光滑的导轨表面形成气膜的部分。这两个单元的弯曲振动是由3个弹性铰链提供的。弹性铰链的作用主要有两个：一是使激振力均匀地分布在单元A上；二是当单元A有位移时，单元B能通过弹性铰链的变形产生挤压运动［10］。

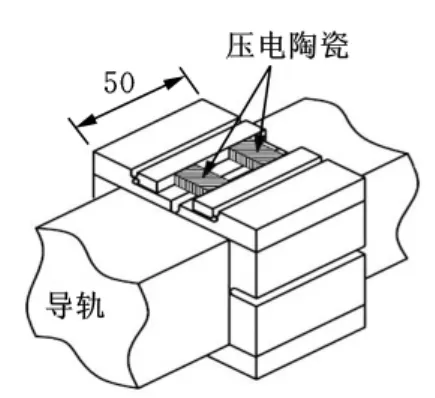
图1 挤压膜轴承机构示意图

图2 轴承实物图

图3 轴承剖面图

如图4所示，当在压电晶体上施加交变电压使其工作在共振状态时，压电晶体能够周期性地伸缩，产生高频振动，使单元A产生一个振动，再通过弹性铰链的作用，使单元B对气隙中的气体进行周期性的挤压，从而形成气体挤压膜，并产生一定的承载能力。在工作过程中，轴承的四个面都将产生气膜压力，上部气膜支承着整个轴承的重量，其他三个面上的气膜起到稳定的作用，使滑块不和导轨接触，减小摩擦力，增加稳定性［11］。

图4 工作原理图

2 应力状态分析

由于该轴承特殊的工作方式，所以有必要对该轴承的应力状况，特别是弹性铰链附近的应力状况进行分析。本轴承材料为铝合金，屈服强度较高。以下是该材料的性能参数：密度2700kg／m3，弹性模量70GPa，泊松比0.33，屈服强度280MPa，轴承质量约为220g。

为了得到轴承在正常工作时的应力分布，本文采用有限元法，利用ANSYS软件对轴承进行压电耦合分析。用ANSYS进行仿真时，加在压电陶瓷电极上面的电压为400V。

从ANSYS分析的结果可以看出（图5），最大的应力集中在弹性铰链的附近，加400V电压所产生的最大应力是6.73MPa，远远小于轴承的屈服强度，所以轴承能承受这样的一个变形。同时，利用ANSYS对应力最大处进行疲劳分析，通过对应力最大的节点的分析，发现该节点的疲劳寿命为3.067×1011次，可近似看作是无穷次，最危险点的寿命是无穷次，说明该轴承不会发生疲劳破坏，满足设计要求。

图5 应力分布状况

3 振动模态分析

为了获得合适的激振振型来提高挤压膜的压力，首先对所设计的轴承进行模态分析，提取前三阶模态，所获得的三阶振型如图6所示。

图6 轴承振动模态

由有限元分析得到该模型的三阶谐振频率为20 136Hz，在这个频率下，轴承能获得更大的变形，并能得到更大的气膜厚度，从而增加该轴承的承载能力。同时，工作在谐振频率下，可以用较低的电压和能耗获得同样的气膜厚度。

4 气膜压力分析

4.1 控制方程

根据轴承的变形情况，可以推导出该挤压膜轴承的理论模型，如图7所示。

图7 气体挤压膜轴承的理论模型

图7是挤压膜导轨正常工作时所产生的挤压膜模型，可以看出这是一个2D矩形挤压膜，可以应用2D矩形挤压膜Reynolds方程进行求解。假设所形成矩形气膜的边长为l0，轴承和轨道之间的原始间隙为hm，施加预紧力的情况下间隙的最大值为h0，轴承正常工作时的振幅为ha。由流体动力润滑理论和几何知识，可以得到挤压膜直线导轨的膜厚方程、运动方程和Reynolds方程。

（1）当0≤x ≤l0／2时，膜厚方程为

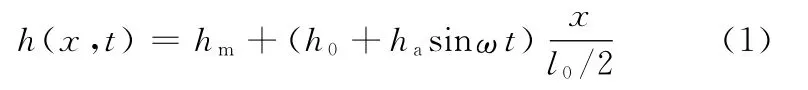
当l0／2≤x≤l0时，膜厚方程为

（2）运动方程为

式中，g为重力加速度；M为滑块质量；t为时间；p为气膜压力；p0为初始压力。

（3）2D矩形挤压膜Reynolds方程为

式中，μ为气体的黏度；ρ为气体的密度。

（4）边界条件为：p｜x，y＝0＝p0；初始条件为：p｜t＝0＝p0，h｜t＝0＝hm。

可以用数值分析法，通过编写Fortran程序对以上方程进行求解，计算出气膜厚度和气膜压力分布［12］。在程序中分别设置电压U 为50V、100V、150V、200V，频率为5000～30000Hz，计算结果如图8所示，从图中可以看出，输入电压越大，气膜厚度就越大。主要原因是因为输入电压增大，陶瓷的振幅就增大，同时轴承的变形也变大，对间隙气体的挤压幅度增加，使膜厚变大。

图8 气膜厚度理论计算值

设环境气压p＝1，则气膜的平均压力可以清晰地从图9看出，第二时段时，负压值最大为0.85，比环境压力低了15%。在第四时段时，气膜的正压力达到最大值，约为环境压力的1.41倍，比环境压力高了0.41倍。所以，在整个工作过程中气膜整体的正压力大于负压力，该气体挤压膜直线导轨具有一定的承载能力。

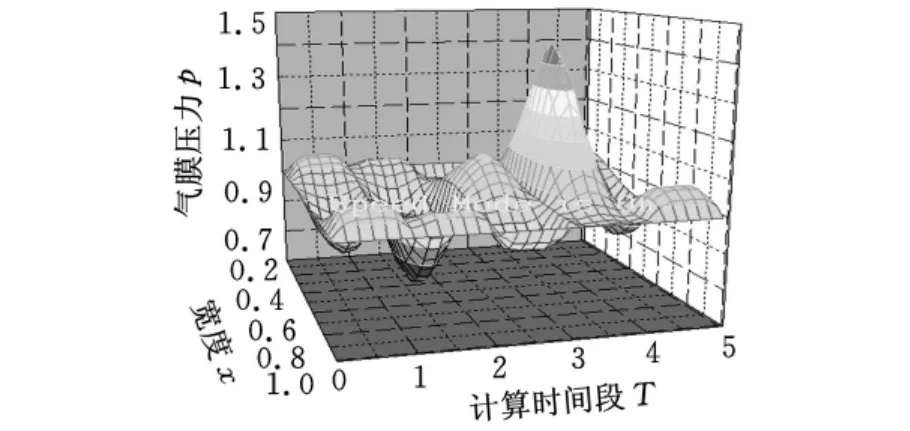
图9 不同时段气膜的平均压力分布

4.2 有限元法分析气膜压力

本文对所设计的轴承的气膜压力分布采用ANSYS软件，从声学角度来进行仿真计算。使用ANSYS对该结构进行电－固－气耦合的声场分析，每个压电片加载正弦电压150V，通过设置载荷的频率范围，可以观察到不同频率下的近场声压分布。图10所示是分别在5kHz、20kHz、50kHz频率下的声压分布，最高声压分别是290Pa、3882Pa、561Pa。可以看出选择在结构模态频率处进行激振可以获得较高的声压。以该弹性铰链滑块在20kHz频率时所产生的近场声压分布，如图10b所示，图上显示铰链滑块受到压电陶瓷的伸展作用，处于被撑开的状态，同时可以看出流体中声波的指向性，以及声场中的近场区、远场区。

图10 50kHz、20kHz、50kHz频率下的声压分布

取图10b中的中轴线上的声场进行分析，绘制出中轴线上的声压情况，如图11所示，可以看出轴线上声压的衰减情况。靠近声源处的声压最大，随着声波传输距离的增大，声压减小。

图11 20kHz频率下轴承法线方向的声压变化曲线

利用ANSYS计算电－固－气耦合情况下的声场，从声学角度解释了气体挤压膜现象，仿真结果可以指导超声悬浮的实验设计，更好地选择激振频率与激振模态，并对实验结果有预期的估计［13］。

5 控制器设计

根据压电陶瓷振子的压电效应原理，轴承工作时需要给压电陶瓷振子输入高频交变电压信号才能使其产生周期性的伸缩运动。由于该轴承没有外部气源，所以必须要设计一个控制器实时改变控制参数。由图8可以看出，在一定频率下，施加到压电片上的电压越大，所产生的气膜厚度就越大，即气膜压力越大。所以控制器采用STC12C5410AD芯片，信号发生电路部分采用高速函数发生器MAX038，自动增益电路的运放采用数字控制的可变增益放大器AD8320。

带超前校正环节的不完全微分PID控制器的传递函数的数学表达式为

式中，Kp为比例系数；Ti为积分时间常数；Tf为滤波器系数为不完全微分环节为超前校正环节［14-15］。

6 系统实验

由控制器、功率放大器、直线导轨、信号采集装置组成的悬浮实验台如图12所示。控制器产生的正弦信号被功率放大器放大后，施加在4块压电陶瓷上，使轴承产生具有承载能力的气体挤压膜。

图12 实验系统

图13 轴承空载时的悬浮高度

给压电陶瓷施加200V的激励信号，使用激光位移传感器对轴承的悬浮高度进行动态测量，结果如图13所示，从图中可以看出，在电压从0连续调至200V的过程中，轴承的悬浮高度随着电压的增大而增大，并最终稳定在一定的范围内，轴承的稳定悬浮高度为10～11μm。将质量为180g的砝码加载到轴承上，将激励信号电压从0连续调节到200V，所测轴承悬浮高度如图14所示，可以看出，有负载时的悬浮高度曲线走势和空载时的走势大致相同。当电压调节到预设值后，轴承同样处于稳定悬浮状态，最终稳定在6.8μm左右。

图14 180g负载下的悬浮高度

7 结论

（1）运用非线性数值解法对2D矩形挤压膜Reynolds方程和弹性变形进行了耦合求解，获得了压力分布、气膜的厚度及气模承载能力；并认为从声学声压的角度也可对气体挤压膜压力及承载能力进行分析。有限元疲劳强度分析结果认为处于高频低幅振动状态下的弹性铰链疲劳强度能够满足设计要求。

（2）通过实验测得在200V激励信号驱动下，弹性铰链气体挤压膜轴承空载以及载荷为180g时的悬浮高度，证明该轴承能够稳定悬浮，并且具有一定的承载能力。

（3）实验测试的悬浮高度低于理论计算值，主要原因是理论模型和实际轴承有一定的区别，如因轴承结构复杂导致的振动响应求解误差，制造、安装误差以及零件的内应力等导致的形状误差等，以及实验测量带来的误差，如残留气膜的影响、干扰信号以及环境振动等带来的误差。

［1］Salbu E O J.Compressible Squeeze Films and Squeeze Bearings［J］.ASME Journal of Basic Engineering，1964，86（3）：355－366.

［2］Minikes A，Bucher I.Coupled Dynamics of a Squeeze－film Levitated Mass and a Vibrating Piezoelectric Disc：Numerical Analysis and Experimental Study［J］.Journal of Sound and Vibration，2003，263：241－268.

［3］贾兵，陈超，赵淳生.基于近场超声悬浮的耦合频率特性分析［J］，中国机械工程，2011，22（17）：2088－2092.Jia Bing，Chen Chao，Zhao Chunsheng.Frequency Characteristics Based on Acoustic Near Film［J］.China Mechanical Engineering，2011，22（17）：2088－2092.

［4］黄明军，周铁英，巫庆华.超声振动对摩擦力的影响［J］.声学学报，2000，25（2）：115－119.Huang Mingjun，Zhou Tieying，Wu Qinghua.The Influence on FricationForce by Ultrasonic Vibration［J］.The Chinese Journal of Acoustics，2000，25（2）：115－119.

［5］Yoshiki H.Near Field Acoustic Levitation of Planar Specimens Using Flexural Vibration［J］.J.Acoust.Soc.，1996，100（4）：2057－2061.

［6］Shigeka Y，Hiroyuki K，Masaaki M.Float Characteristics of a Squeeze－film Air Bearing for a Linear Motion Guide Using Ultrasonic Vibration［J］.Tribology International，2007，40（3）：503－511.

［7］Stolarski T A.Load－carrying Capacity Generation in Squeeze Film Action［J］.International of Mechanical Sciences，2006，48（1）：736－741.

［8］Stolarski T A.Numerical Modeling and Experimental Verification of Compressible Squeeze Film Pressure［J］.Tribology International，2010，43：356－360.

［9］常颖，彭太江，阚君武，等.超声振动对摩擦系数影响的试验研究［J］.压电与声光，2003，25（6）：86－89.Chang Ying，Peng Taijiang，Kan Junwu，et al.Experiment Study on the Influence on Friction－factor by Ultrasonic Vibration［J］.Piezoelectrics and Acoustooptics，2003，25（6）：86－89.

［10］Stolarski T A，Wei Chai.Self－levitating Sliding Air Contact［J］.International Journal of Mechanical Sciences.2006，48（1）：601－620.

［11］常颖，吴伯达，程光明，等.超声波轴承用压电换能器模态分析及实验研究［J］.哈尔滨工业大学学报，2006，38（5）：752－754.Chang Ying，Wu Boda，Cheng Guangming，et al.Model Analysis and Experiment Study on the Piezoelectric Transducer［J］.Journal of Harbin Institute of Technology，2006，38（5）：752－754.

［12］Stolarski T A，Woolliscroft S P.Performance of a Self－lifting Linear Air Contact［J］.Proc.IMechE，Part C：J.Mechanical Engineering Science，2007，221（5）：1103－1115.

［13］魏彬.超声激励的气体挤压膜线型导轨理论及实验研究［D］.南京：南京航空航天大学，2009.

［14］陶永华.新型PID控制及其应用［M］.北京：机械工业出版社，2002.

［15］姜宏伟.基于TMS320F28335DSP的磁悬浮系统数字控制器研究［D］.南京：南京航空航天大学，2010.