任务负载竞争下制造资源配置的非合作博弈方法

陈 冰 刘 凯 杨 挺

西北工业大学现代设计与集成制造技术教育部重点实验室，西安，710072

0 引言

以汽车、飞机、航空发动机、船舶等为代表的离散制造业在其零件生产过程中具有工艺复杂、品种多、批量小、批次多、难度大、特种工艺多的特点，大多采用在一定时间内，同一条生产线上生产多种不同型号、不同数量产品的多品种混流生产的生产组织模式［1］，为此，生产线中设备大都需要承担不同种类零件的生产任务。在生产线中往往以设备利用率作为对设备服役过程的考核指标，每台设备在生产过程中，都希望有较高的设备利用率，因此，在生产过程中不同设备之间存在对制造任务的竞争关系。设备与任务之间的关系就是制造资源的配置问题。传统的资源优化配置主要从任务调度方面进行研究，以车间或者单元为研究对象，实现制造任务向车间或者单元的生产设备分配［2-6］。这样的资源配置方法忽略了生产设备之间存在的追求任务负载的竞争关系，从而不能保证设备的利用率获得最大程度的提高，最终导致资源浪费。

为此，在本文中把每台设备作为决策主体来描述它们在生产过程中的相互竞争关系，在制造过程中，以每台生产设备的利用率为收益函数，建立制造资源配置的非合作博弈模型，并通过对局中人的模糊聚类实现对模型的求解，进而实现制造资源的优化配置。

1 设备配置过程的形式化描述

本文所研究的是将制造任务加载到具体生产设备的过程，为此，首先进行如下假设：①在同一时间，一台设备只能完成一个零件一道工序的生产任务；②所有的生产设备有相同的机会竞争加工任务。

设备配置过程中涉及的主要元素包括制造工艺、生产设备等，它们可以形式化描述如下：

（1）生产设备E ＝｛Ei，i＝1，2，…，n｝，表示生产线中的n个生产设备。

（2）可用时间Ta＝｛Ta，i，i＝1，2，…，n｝，表示生产设备能够用于生产的时间。

（3）制造工艺Pr＝｛Pr，ij，i＝1，2，…，m；j＝1，2，…，Ni｝，其中，i 为零件的序号，j 为零件Pi的工序号，Ni为工艺路线所包含的工序数，Pr，ij表示零件Pi的第j道工序。此外，Pi的第j道工序的工时可以表示为Tij。

（4）任务负载L＝｛Li，i＝1，2，…，n｝，表示在制造任务加载到生产设备之后，其所承担的工序对应工时的总和。

（5）设备利用率U＝｛Ui，i＝1，2，…，n｝，表示生产设备的利用率，等于任务负载与可用时间的比值，即

2 制造资源优化配置非合作博弈数学模型

2.1 博弈论与非合作博弈

博弈论是研究决策问题及均衡问题的理论。非合作博弈是指所有局中人选择各自策略以求得自身利益最大化的过程。规范型的非合作博弈问题包括三个要素：局中人（player），策略集 （strategy），收益函数（payoff）［7］。

2.2 制造资源配置的非合作博弈模型

在本文的制造资源配置的非合作博弈过程中，参与制造的生产设备映射为博弈模型中的局中人，与生产设备相关的制造任务工序映射为策略集，将生产设备的利用率作为局中人的收益函数，通过求解该模型的Nash均衡［7］，就可完成制造资源的优化配置，提高设备利用率，促进设备之间的负载均衡，降低设备运行成本，使得任务负载和资源配置更趋合理。

针对上述资源配置模型，引入博弈论，那么制造资源配置的非合作博弈模型可以用如下三元组进行描述：

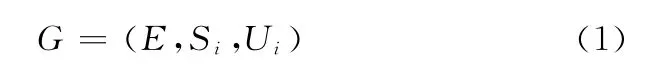
上式的变量描述如下：

（1）假设有n台可用设备，局中人为E＝｛E1，E2，…，En｝。

（2）Si为局中人Ei的策略集，即设备可承担的可选任务。生产线中所有设备局中人的可选任务集为S｛Si（Pr，i，Ti）｝，i＝1，2，…，n。 假设局中人Ei的策略集Si包括k个策略，则Si＝｛（Pr，ij，Tij）｝，i＝1，2，…，n；j＝1，2，…，k。

（3）Ui为设备局中人的收益函数，即为生产设备的利用率。

3 基于模糊聚类的博弈模型求解方法

寻找博弈论的解是博弈论的核心内容，针对多个局中人博弈模型的问题，本文引入模糊聚类理论对局中人进行聚类分析［8-9］，把多个局中人分为两组，将多人博弈的模型转化为两人博弈模型，从而降低博弈求解的难度。

3.1 博弈局中人的模糊聚类方法

模糊聚类分析应用模糊数学方法进行聚类分析，因此模糊聚类分析可以将各个样本以不同的隶属度划分到各个类别，即将样本对各个类的隶属度扩展到区间［0，1］，以数字定量地确定样品的“亲疏关系”，从而将样品进行分类划分［10］。

本文采用模糊等价关系的聚类分析，将不同的博弈局中人进行归属分类。在聚类分析之前，需要明确局中人之间的关系，可以引申为模糊数学的模糊关系。数学上用“关系”来描述事物之间的联系，在模糊数学中用集合的形式来表示“关系”。如果不仅仅只有两种事物，那么每两种事物将会构成一个模糊关系集合，所有模糊关系的集合构成一个模糊关系矩阵R＝（rij）n×n。模糊关系矩阵可以描述设备局中人策略空间的相似程度，便于归属分类，从而简化博弈模型求解。通常情况下计算得到的模糊矩阵满足自反性及对称性，但是不满足传递性。为了能够对设备局中人进行归属分类，需要对模糊矩阵进行合成运算，使模糊矩阵满足模糊关系矩阵性质。

根据非合作博弈模型，基于模糊聚类分析对设备局中人进行聚类，完成策略空间的归属。模糊聚类分析的过程首先是建立模糊聚类分析的样本，通过消除样本的量纲把样本的隶属度控制在［0，1］区间之内，最后建立模糊相似矩阵，并对模糊相似矩阵进行合成运算，求得其传递矩阵，最后根据传递矩阵来归属聚类。

在整个聚类过程中，建立模糊相似矩阵的方法有很多种，常用的有：夹角余弦法、相关系数法、最大最小法、数量积法、算术平均最小法、几何平均最小法、绝对值指数法、绝对值倒数法、绝对值减法等。根据设备局中人的特点，这里选择绝对值减法来建立模糊相似矩阵，具体实现步骤如下：

（1）模糊聚类分析的初始样本表征的是设备局中人在其策略空间中描述加工每道可选加工工序的利用率，可以使设备局中人能够“理性地”争取自身利用率最大的工序，避免承担自身利用率较低的工序。通过建立初始样本，可以使得设备局中人一开始就谋求自身利用率最大化，同时也便于具有相似策略空间的设备局中人的聚类归属。此外，根据初始样本的特征，可以把样本的隶属度控制在［0，1］区间内，便于构建模糊相似矩阵。

（2）由于建立的样本隶属度在［0，1］区间内，因此不需要再进行标准差变换及极差变换来消除量纲对模糊相似矩阵的影响。为此，首先对每一台生产设备Ei用每道工序在该设备能够消耗的工时来表征，即（xi1，xi2，…，xiM），其中 M 是所有零件所包含工序数量的总和，即然后，建立模糊相似矩阵R＝（rij）n×n，其中0≤rij≤1，i，j＝1，2，…，n。这里rij表示对象Ei与Ej的相似程度，且

式中，C为适当选取的系数，使0≤rij≤1。

（3）将标定所得的模糊矩阵R改造成模糊等价矩阵R＊，即使得R满足模糊关系矩阵的性质。常用平方法求得R的传递闭包，依次计算R2，R4，R8，…，R2i，当满足R＊＝R＊·R＊时，R＊即为R的传递闭包矩阵。

（4）对传递闭包矩阵R＊，取模糊分类隶属度λ由大变小，即从1到0，可以把不同的设备局中人进行归属分类，形成动态聚类图，从而减少局中人的策略归属空间，简化博弈模型求解。

3.2 博弈模型纳什均衡最优解

对于局中人Ei的策略si和s′i，当且仅当ui（si，s－i）＞u（s′i，s′－i）对于任意s－i∈S－i都成立时，称前者对于后者是严格优势的。如果ui（si，s－i）≥u（s′i，s′－i），且至少有一个s－i使不等式严格成立时，则称纯策略si为弱优势。一般地，博弈论中将除了某个给定的局中人之外的所有局中人标记为“－i”。

在博弈过程中，局中人通过竞争与合作，最终会达到利益均衡，那么这个均衡就是博弈论的解。1950年约翰·纳什（John Nash）定义了非合作博弈模型及其均衡解。这个均衡理论被称为纳什均衡（Nash Equilibrium）。纳什均衡可以用数学的方式描述如下：

纳什均衡实际上是一组所有局中人策略的组合，它使得每个局中人的策略都是对其他局中人策略的最优反应，即任何一个局中人单独偏离纳什均衡，其自身收益不会因此而变大；相反，如果存在这么一种均衡不是纳什均衡，即不是所有参与者的最优策略组合，至少会有一个局中人会改变自己的策略来谋求更好的收益，那么这种均衡不具有“自我约束力”，就不能达到一种稳定而且持久的平衡。

如前所述，在整个博弈的过程中，博弈的结果不仅受到局中人所选策略的影响，还将受到其他局中人策略的影响，即任何一个局中人的收益都取决于所有局中人的策略组合。在某一次博弈过程中，如果某个局中人的某一种策略对于其他策略总是严格优势或者弱优势的，那么该局中人会乐于接受这种策略选择。推广开来，如果某种策略组合对于其他策略组合是严格优势或者弱优势的，那么所有的局中人都将乐于接受这种策略组合，因此是稳定的，即达到了Nash均衡。

对于有限个局中人博弈，Nash均衡并不唯一。对于Nash均衡的多重性问题，一般的解决方法是采用均衡精炼的方法。常用的均衡精炼方法主要有帕累托（Pareto）改进与风险占优两种方法，本文采用的是帕累托改进的方法。即

考虑博弈G＝（N，Si，Ui），对于任意给定的两种策略组合s∈Si，如果：①｛i∈N：ui）＞ui（s）｝≠ ∅，② 对于任意一个i∈N，都有ui）≥ui（s），则称为s 的一个帕累托改进。对于策略组合而言，如果不存在其他策略组合为其帕累托改进，那么称策略组合为帕累托最优。

4 算例分析

4.1 非合作博弈模型实例

为了验证资源优化配置非合作博弈模型的有效性及可行性，以拥有8台设备，承担7种不同零件生产任务的生产线为实例进行验证计算。

表1中给出了设备可承担的工序集合。从表中可以看出设备E2可以承担的工序集合可以表示 为 ｛Pr，11，Pr，15，Pr，24，Pr，33，Pr，41，Pr，45，Pr，47，Pr，56，Pr，62，Pr，71，Pr，73｝，此外，每道工序在对应设备上的工时在圆括号中给出。例如工序Pr，11在E2上的工时为7.2h。表1中给出的工序集合就是生产设备的博弈策略空间，其策略只能从该策略空间中选择，通过预测他人的策略选择来确定自己的策略，以谋求自身利益最大化，显然，Nash均衡解也必定落在这个工序集合之内。

表1 设备可加工工序集h

4.2 基于模糊聚类的博弈模型解算

从表1可知，博弈局中人N＝8，即为｛E1，E2，E3，E4，E5，E6，E7，E8｝，构成8 人的多人博弈模型。这种多人博弈模型中Nash均衡的求解是非常困难的。为此，本文引入模糊聚类算法来对局中人进行聚类分析，以减少局中人的个数，这样可以大大降低博弈模型的求解难度。

首先对每个局中人（设备）Ei用每道工序在该设备能够消耗的工时来表征，即（xi1，xi2，…，xiM），例如设备E1的隶属度值为

同样对其他设备进行表征，并采用绝对值减法，｜C｜＝0.02，求得模糊相似矩阵为

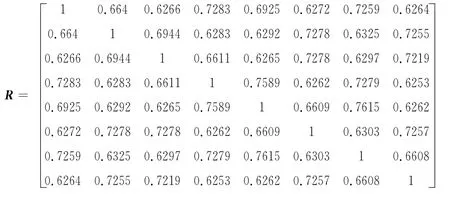
采用平方法来求布尔矩阵R的传递闭包矩阵：

由于R4＝R8，因此矩阵R的传递闭包矩阵t（R）＝R4。当λ＝0.7时，把8个局中人（设备）分为两组，即P1＝｛E1，E4，E5，E7｝，P2＝｛E2，E3，E6，E8｝。经过归属后，P1、P2的策略空间分别为

通过对比分析P1与P2的策略空间，把只能由生产设备组P1（P2）加工的工序称为P1（P2）的固有策略，这些固有策略并不因为生产设备组的博弈过程而改变，也不存在固有设备组之间的竞争。由于固有策略的特殊性，需要对其进行特殊的处理。把P1和P2的固有策略提取出来，其中，P1的固定策略为

P2的固定策略为

通过划分，博弈模型变为二人博弈。但是存在一个问题，P1及P2的固定策略是由其组员共同承担的，对于具体设备的配置就需要先对P1及P2的固定策略进行博弈解算，同时可以得到生产设备组P1及P2在其固定策略上的设备利用率，才能使P1、P2间的博弈能够进行下去。

对P1的固有策略来说，对其进行模糊聚类分析，求得模糊相似矩阵及其传递闭包矩阵为

同样地，对P2的固有策略进行模糊聚类分析，可以求得其模糊相似矩阵以及传递闭包矩阵，即

博弈的结果是双方相互作用的结果，任何一个局中人改变其策略，双方的收益都会发生变化。需要注意的是，当局中人E1与局中人E4选择的策略中包含相同的工序时，此时双方的利用率收益均为零。根据之前假设的条件及博弈模型的约束可以知道，在实际加工过程中，同一个工序不能同时被两台生产设备加工，同时生产设备并不区分优势弱势，均具有相同的机会申请加工该道工序，因此不能说明发生冲突的工序应该由哪台设备进行加工，由此双方局中人的收益均为零。

4.3 Nash均衡的求解

用相同的方法继续对设备组P1和P2的固定策略划分为不同的子博弈模型，计算其利用率收益并对加工工序进行策略归属，可以得到设备局中人的策略空间归属。表2列出了设备组P1和P2固定策略经过博弈后，各设备局中人的策略空间。

表2 设备局中人在固定策略下的策略归属

在完成了对设备组P1和P2的固定策略的策略归属之后，把它们对应的策略表示为OP1和OP2，再来对设备组P1和P2进行博弈解算。设备组P1和P2的收益矩阵如表3所示。

表3 P1和P2的收益矩阵

根据收益矩阵采用基于启发搜索算法［11］其Nash均衡计算过程如图1所示。此时P1选择策略P1（OP1Pr，25Pr，51Pr，77），P2选择策略P2（OP2）。图1显示了P1和P2纯策略Nash均衡帕累托改进的收敛曲线。

图1 P1和P2纯策略Nash均衡帕累托改进的收敛曲线

为了便于分析问题，把P1和P2的其他纯策略Nash均衡做了隐藏处理。由图1可以看出，博弈双方由于不知道对方会选择什么样的策略，因此一开始均以12.5%的概率来选择8组纯策略进行组合作为本方策略选择，即以混合策略的形式来选择策略。随着博弈活动的进行，P1发现如果选择策略，P2发现如果选择策略，那么他们的利用率收益都会变大。但是由表3可以看出，如果双方采取的策略组为的话，此时并不稳定，即只要双方任何一个人改变其策略，都会找到更好的收益。策略组并不是它们的Nash均衡点，是不具有任何的“自我强制性”的。博弈活动继续深入进行，此时局中人P1知道，P2在这次博弈的活动中会一直选择策略，如果自己不改变策略将会得到较小的收益，因此P1最后放弃了本来能够得到更好收益的策略，转向采取了收益较差的策略，最终达到了Nash均衡。由表2及表3可以看出，博弈的结果是局中人双方相互作用的结果，是双方进行竞争而产生的结果，竞争的结果不可能达到双方都是严格优势的均衡解，但是一定是严格弱优势的均衡解。

将P1和P2的策略归属到8台生产设备E1，E2，…，E8上来，我们可以得到8台设备局中人进行博弈后最终的策略选择。表4为各局中人E1，E2，…，E8的策略选择及其收益。

表4 局中人策略选择及收益

5 博弈方法与遗传优化算法的比较

为了验证博弈模型及解算结果的正确性及有效性，将本文提出的博弈算法与常用的遗传优化算法（genetic algorithm，GA）、禁忌搜索（tabu search，TS）和粒子群算法（particle swarm optimization，PSO）进行比较分析。遗传算法一般由选择、交叉、变异三种进化算子组成。对于选择算子，采用轮盘赌的方法进行；对于交叉算子，采用单点交叉的方法；对于变异算子，与传统的变异算子相同，有所区别的是变异的规则或者说变异的范围要进行控制。由于加工任务由一系列的加工工序组成，当发生变异时，则在具有相同加工能力的设备间发生变异。由此，在本文的实例中以种群规模为50，交叉概率为80%，变异概率为5%条件下进行遗传运算，在最大迭代次数为2000时进化终止。对于禁忌搜素算法采用禁忌长度为10、候选集长度为15，最大迭代次数为200作为搜索参数。粒子群算法的参数设置为：粒子维数（即设备数）D＝8，粒子规模（即粒子数）Xnum＝16，加速系数c1＝2.2，c2＝1.6。将博弈方法与遗传算法、禁忌搜算、粒子群算法的优化结果在表5中进行比较，可以看出博弈方法在优化效果上优于遗传算法。

表5 优化结果比较

6 结论

针对制造资源的优化配置问题，引入博弈论描述设备之间在任务负载上的自由竞争关系。以设备最大利用率为收益函数，构建了基于非合作博弈论的资源优化配置数学模型，并根据模糊数学的模糊聚类分析理论提出了求解博弈模型Nash均衡的算法。最后通过实例并与遗传算法、禁忌搜算、粒子群算法进行比较，验证了本文提出的非合作博弈资源优化配置模型及求解方法的有效性和正确性。

［1］王炳刚，饶运清，邵新宇，等.基于多目标遗传算法的混流加工／装配系统排序问题研究［J］.中国机械工程，2009，20（12）：1434－1438.Wang Binggang，Rao Yunqing，Shao Xinyu，et al.A MOGA－based Algorithm for Sequencing a Mixed－model Fabrication／Assembly System［J］.China Mechanical Engineering，2009，20（12）：1434－1438.

［2］郑永前，王阳.基于遗传算法的加工工艺决策与排序优化［J］.中国机械工程，2012，23（1）：59－65.Zheng Yongqian，Wang Yang.Optimization of Process Selection and Sequencing Based on Genetic Algorithm［J］.China Mechanical Engineering，2012，23（1）：59－65.

［3］Ma G H，Zhang Y F，Nee A Y C.A Simulated Annealing－based Optimization Algorithm for Process Planning［J］.International Journal of Production Research，2000，38（2）：2671－2687.

［4］潘全科，朱剑英.多工艺路线多资源多目标的作业调度优化［J］.中国机械工程，2005，16（20）：1821－1826.Pan Quanke，Zhu Jianying.An Optimization Method for a Multi－objective Job－shop Scheduling Problem under Multi－resource Constraints［J］.China Mechanical Engineering，2005，16（20）：1821－1826.

［5］Wong T N，Leung C W，Mak K L，et al.Dynamic Shop Floor Scheduling in Multi－agent Manufacturing Systems［J］.Expert Systems with Applications，2006，31（3）：486－494.

［6］Li W D.A Simulated Annealing－based Optimization Approach for Integrated Process Planning and Scheduling［J］.International Journal of Computer Integrated Manufacturing，2007，20（1）：80－95.

［7］侯定丕.博弈论导论［M］.合肥：中国科学技术大学出版社，2004.

［8］郑丞，金隼，来新民，等.基于非合作博弈的公差分配优化［J］.机械工程学报，2009，45（10）：159－165.Zheng Cheng，Jin Sun，Lai Xinmin，et al.Tolerance Allocation Optimization Based on Non－cooperative Game Analysis［J］.Journal of Mechanical Engineering，2009，45（10）：159－165.

［9］范周田.模糊矩阵理论与应用［M］.北京：科学出版社，2006.

［10］张弢，纪德云.模糊聚类分析法［J］.沈阳大学学报，2000，12（2）：73－79.Zhang Tao，Ji Deyun.Fuzzy Clustering Analytical Methods［J］.Journal of Shenyang University，2000，12（2）：73－79.

［11］隗立涛，修乃华.基于启发搜索算法的纳什均衡计算［J］.北京交通大学学报，2007，31（3）：58－62.Wei Litao，Xiu Naihua，Computing Nash Equilibria Based on Heuristic Search Methods［J］.Journal of Beijing Jiaotong University，2007，31（3）：58－62.