局部特征尺度分解方法及其分量判据研究

杨 宇 曾 鸣 程军圣

湖南大学汽车车身先进设计制造国家重点实验室，长沙，410082

0 引言

自适应时频分析方法的特点主要表现在不需要对被分析信号的形态特征或者信息做出预测和限制的前提下，可以在对信号进行分解的过程中根据信号本身的特性自动产生基线信号，从而使得分解结果具有一定的物理意义。近年来最具代表性的自适应时频分析方法是经验模态分解（empirical mode decomposition，EMD）方法［1-2］，该方法在定义瞬时频率具有物理意义的内禀模态函数（intrinsic mode function，IMF）分量的基础上，通过上下极值点包络线的平均来构造基线信号，从而将复杂的多分量信号自适应地分解为若干个IMF分量之和。由此可见，自适应时频分析方法的关键在于基线信号的构造。

文献［3］介绍了一种新的基线信号构造方法，即以原始信号任意两个相邻的极值点为跨度对信号进行分段线性变换来构造基线信号，且由此提出了内禀时间尺度分解（intrinsic time－scale decomposition，ITD）方法，并将其应用于脑电波癫痫信号的分析。ITD方法每次只经过单步迭代就得到固有旋转分量（proper rotation component，PRC），即将基线信号从原始信号中分离后得到的剩余信号作为PRC分量，并将基线信号作为下一次迭代的原始信号，如此循环下去就可将信号分解为若干PRC分量之和。由于对于脑电波癫痫信号采用单步迭代分解就能得到有意义的分量，因此文献［3］并没有研究PRC分量的判据。

而对于一般的振动信号，单步迭代分解并不能保证分解出来的分量有意义，因此，本文在对ITD方法进行研究的基础上提出了一种新的自适应时频分析方法——局部特征尺度分解（local characteristic－scale decomposition，LCD）方法。该方法采用ITD方法中基线信号的构造方法，通过多次迭代自适应地将信号分解为若干个瞬时频率具有物理意义的内禀尺度分量（intrinsic scale component，ISC）。LCD方法要分解出正确的ISC分量，首要的问题即为确定ISC分量的判据。对于ISC分量判据研究，可以参考EMD方法中一些主要的判据，如标准差判据［1］、S值判据［4］、三参数法［5］和能量差跟踪法［6］等。本文将EMD方法中最常用的标准差判据应用于LCD方法，而标准差判据的阈值会因自适应时频分析方法的不同而有所差异（EMD方法中标准差判据的阈值为0.2～0.3［1］），因此本文通过大量数据试验确定适用于LCD方法的标准差判断的阈值。对于不同的自适应时频分析方法，标准差判据的适用阈值也不同，且在被应用之前都需要经过数据试验以确定合理的阈值，并不具备自适应性。为了克服这一缺陷，本文在对瞬时频率具有物理意义的典型信号的时域形态进行研究的基础上提出了一种新的具有自适应性的分量判据——极值单调性判据，该判据无需设定任何阈值，仅仅依赖瞬时频率具有物理意义分量的客观存在的极值单调性。信号分析结果表明这两种判据都可应用于LCD方法，而极值单调性判据具有自适应性，其适用性更强，能直接应用于EMD方法。此外，本文还对LCD方法和EMD方法的计算效率进行了对比分析，结果表明LCD方法在计算效率方面要优于EMD方法。

1 LCD方法

1.1 ITD方法基线信号的构造

ITD方法采用分段的形式对信号任意两个相邻的极值点之间的数据段进行线性变换而获得基线信号。

设原始信号x（t）的极值为Xk（k＝1，2，…，M），其对应的时刻为τk（k＝1，2，…，M），如图1中“·”所示。 由任意两个极大（小）值点（τk，Xk）、（τk＋2，Xk＋2）连接形成的线段在其中间极小（大）值点（τk＋1，Xk＋1）对应时刻τk＋1的值为

这样可在点（τk＋1，Ak＋1）与（τk＋1，Xk＋1）之间用线性插值得到基线信号控制点（τk＋1，Lk＋1）的纵坐标值：

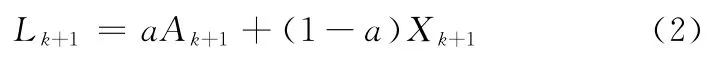
其中，a ∈ （0，1）为一常量，典型地，可取a＝1／2。图1中“▲”所示即为基线信号控制点。

基线信号控制点对应的时刻τk（k＝1，2，…，M）将原始信号x（t）分割成若干个区间，在任意两个相邻极值点之间对x（t）进行线性变换：

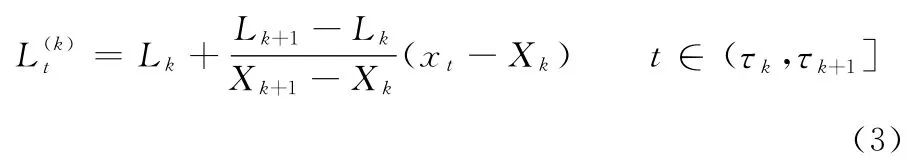
图1 ITD方法中基线信号的构造

1.2 LCD方法分解过程

LCD方法假设任何复杂信号由不同的ISC分量组成，任何两个ISC分量之间相互独立，这样，一个多分量信号x（t）就可以被分解为有限个ISC分量之和，其中任何一个ISC分量满足以下条件：①在整个数据段内，任意两个相邻极值点符号互异；②在整个数据段内，其极值点为Xk（k＝1，2，…，M），各个极值点对应的时刻为τk，由任意两个极大（小）值点（τk，Xk）、（τk＋2，Xk＋2）连接形成的线段在其中间极小（大）值点（τk＋1，Xk＋1）对应时刻τk＋1的函数值Ak＋1与该极小（大）值Xk＋1的比值关系近似不变。

根据所定义的ISC分量，对信号x（t）进行LCD方法分解，可将其分解为若干个ISC分量之和，分解过程如下：

（1）确定原始信号x（t）的所有极值点（τk，Xk），利用式（1）～ 式（3）构造基线信号

（2）将m11（t）从原始信号中分离出来，得到剩余信号

理想地，如果h11（t）满足ISC分量判据，则h11（t）为信号x（t）的第一个分量ISC1（t）；如果h11（t）不满足ISC分量判据，将h11（t）作为原始信号，重复步骤（1），则循环i次得到剩余信号h1i（t）＝h1i－1（t）－m1i（t），使得h1i（t）满足ISC分量判据，h1i即为信号x（t）的第一个分量ISC1（t）。

（3）将ISC1（t）从原始信号中分离出来，得到

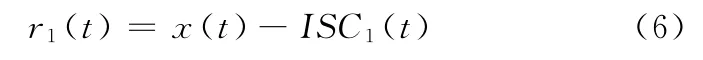
将r1（t）作为原始信号，重复步骤（1）、（2），得到x（t）的满足ISC分量判据的第二个分量ISC2（t），重复循环n次，得到信号x（t）的n个满足ISC分量判据的分量，直到rn（t）为一单调函数或者小于预设阈值为止。这样便可以将x（t）分解为n个ISC分量和一个剩余函数rn（t）之和，即

通过上述步骤，LCD方法可将一个多分量信号分解成若干ISC分量之和。与ITD方法相比，LCD方法在每次迭代过程中都对剩余信号进行分量判定，并通过多次迭代自适应地获得ISC分量。

与EMD方法相比，LCD方法通过对原始信号本身进行分段线性变换来得到基线信号，而EMD方法的基线信号只是通过信号上下极值点包络线的平均来获取，并没有充分用到原始信号数据，因此LCD方法中的基线信号能更有效地获得原始信号的内在本质特征［3］。另外，LCD方法还避免了EMD方法采用三次样条插值形成上下包络线时可能产生的过包络、欠包络问题［7］。

1.3 仿真信号分析

考察如下所示仿真信号（采样频率2048Hz，t∈［0，1］s）：

仿真信号x（t）由调幅调频信号x1（t）和调幅信号x2（t）合成，其时域波形如图2所示。

图2 仿真信号x（t）的时域波形

对信号进行ITD方法分解，分解结果如图3所示。由该分解结果可以明显地看出，第一个分量PRC1是没有意义的分量，它不能反映原始信号中的调幅调频成分。对于一般的信号，ITD方法中单步迭代分解并不能保证分解出来的分量有意义，其使用范围有限。

图3 仿真信号的ITD方法分解结果

对信号进行LCD方法分解，初步设置单个分量迭代次数n＝6，分解结果如图4所示。由该分解结果可以看出，分量ISC1和ISC2分别对应着原始信号中调幅调频信号x1（t）和调幅信号x2（t），基本上能正确地反映出原始信号的成分特征。对比ITD方法，LCD方法的分解结果更准确。

图4 仿真信号的LCD方法分解结果

2 分量判据研究

2.1 标准差判据

对于ISC分量判据研究，可以参考EMD方法中常用的标准差判据，即采用单个分量迭代过程中连续两次迭代结果的标准差作为迭代终止条件［1］：

式中，T为信号长度。

当标准差SD达到某一给定阈值时则可认为迭代结束。为确定合理的标准差阈值，采用LCD方法对不同类型的仿真信号（如正弦、调幅、调频以及调幅调频等信号之间的相互叠加）进行分析。LCD方法首先将频率相对较高的分量分离出来，因此可将获取高频分量的迭代过程作为研究对象，计算每次迭代的SD 值，并以均方误差MSE作为分解效果的评价指标。下面仅给出由正弦和线性调频叠加而成的仿真信号试验数据。正弦和线性调频叠加而成的仿真信号模型为

式中，a1、a2、f1、f2和f3均为模型参数。

改变模型参数得到6组参数：

分别在上述6组参数下各迭代10次得到的实验数据如表1所示。观察表1中数据，当各组参数下的SD 值分别满足条件：①SD ＜0.012357612；②SD ＜ 0.046731089；③SD ＜0.158971762；④SD ＜ 0.430891421；⑤SD ＜0.172266713；⑥SD ＜0.018564477，则不同参数下的MSE相对来说都能够取得较小值，因此对于式（10）所表示的仿真信号可取阈值SD ＜0.012357612。各类型仿真信号模型都有一个合适的标准差阈值使得在该模型不同参数下的MSE都能够取得较小值，因此可取这些标准差阈值的交集作为LCD方法标准差判据的总阈值。

综合各类型的仿真信号实验数据，可以给出一个较为合理的标准差阈值：SD＜0.01。这个标准差阈值并不包括下限，一般说来，经过多次迭代得到较好分解效果时，当次迭代SD值已经很小了，接近于0（由表1也可以看出），因此没有必要再设置SD的下限值。

2.2 极值单调性判据

极值单调性判据是本文提出的一种新的具有自适应性的分量判据。首先研究瞬时频率具有物理意义的典型调幅调频信号，其时域波形如图5所示，给图中极值点编序号。

表1 标准差判据研究中的部分实验数据

图5 瞬时频率具有物理意义的典型信号

将信号为负的部分取绝对值，如图6中的虚线所示。观察图形可以发现，这些离散的极值点在时间尺度上不易发现其规律性，但它们在一定的极值点序列区间内存在单调性，如第6个至第11个极值点呈现单调递增，第11个至第16个极值点呈现单调递减，其中第11个极值点是极值点中的极大值点（可称为二级极大值点），而第6和第16个极值点是极值点中的极小值点（可称为二级极小值点）。这种离散的极值点序列所存在的单调性应当是瞬时频率具有物理意义的分量的固有特性，利用这一特性可以近似进行分量判定，判定思路如下：

图6 信号为负的部分取绝对值

（1）找出信号极大值点和极小值点，并保证极大值严格为正，极小值严格为负。

（2）确定由极大值点所产生的二级极值点，包括二级极大和极小值点。

（3）将二级极大值点与其前后相邻两个极值点（极大或者极小值点）进行绝对值大小比较，取三者中较大者作为新的二级极大值点，同理，将二级极小值点与其前后相邻两个极值点（极大或者极小值点）进行绝对值大小比较，取三者中较小者作为新的二级极小值点。

（4）对所有极小值点取绝对值，使得所有极值点序列均为正。

（5）找出由步骤（3）确定的相邻两个二级极值点分割所确定的极值点序列，并判断这两个相邻的二级极值点的大小：①若前者小于后者，则该组极值点序列应当是单调递增；②若前者大于后者，则该组极值点序列应当是单调递减；③若两者相等，则该组极值点序列应当是等值的。若信号满足①、②和③中的一项，则可以认为该信号是瞬时频率具有物理意义的分量。

现以图5中调幅调频信号为例说明极值单调性判定思路：

（1）极大值点已经严格为正，极小值点已经严格为负。

（2）若暂不对端点进行极值点定义，则正的极大值点所确定的二级极大值点为第11个极值点，二级极小值点分别为第5（或第7）和第15（或第17）个极值点。

（3）将第5个极值点（二级极小值点）与第4和第6个极值点进行绝对值大小比较，取绝对值较小的第6个极值点作为新的二级极小值点，同理可取第11个极值点作为新的二级极大值点，取第16个极值点作为新的二级极小值点。

（4）对信号为负的部分取绝对值使得极值点全为正。

（5）第6个极值点（二级极小值点）小于第11个极值点（二级极大值点），则该组极值点序列6、7、8、9、10和11应当是单调递增，如图6所示。其他极值点序列判定方法类似。

假设在上述步骤（5）中，第8个极值点大于第9个或者第10个极值点，即第6至第11个极值点区间内极值点序列不是单调递增，那么在图5中，我们可以直观地感觉到该信号在第8个极值点附近不具有局部对称性。

对于极值取绝对值后整个极值点序列呈单调性（如线性调幅信号）或者整个极值点序列保持为一个常值（如正弦信号）的信号，极值单调性判定方法依然适用。

极值单调性判据无需设定阈值，仅仅依赖瞬时频率具有物理意义分量的客观存在的极值单调性。满足极值单调性判据的分量应该具有局部对称性，其上下包络平均应当接近零。

2.3 分量判据有效性验证

2.3.1 仿真信号分析

为了验证前面给出的标准差判据和极值单调性判据的有效性，考察如下所示仿真信号（采样频率2048Hz，t∈［0，1］s）：

仿真信号x（t）由调幅调频信号x1（t）、调幅信号x2（t）和正弦信号x3（t）合成，其时域波形如图7所示。下面分别采用上述两种分量判据对信号进行LCD方法分解。

图7 仿真信号x（t）的时域波形

采用标准差判据对信号进行LCD方法分解，分解结果如图8所示。采用极值单调性判据对信号进行LCD方法分解，分解结果如图9所示。从理论上分析，调幅调频信号x1（t）负的极小值点取绝对值后的所有极值点序列既存在单调递增又存在单调递减的序列区间；调幅信号x2（t）负的极小值点取绝对值后的整个极值点序列就是一个单调递减的序列；正弦信号x3（t）负的极小值点取绝对值后的所有极值点序列是一个常值序列。

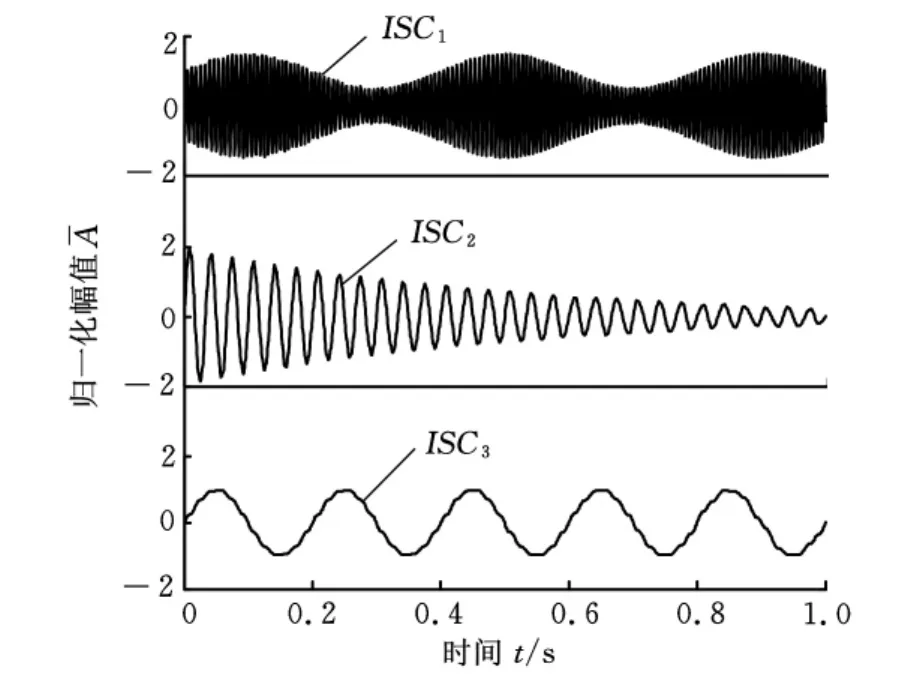
图8 LCD方法分解结果（标准差判据）

图9 LCD方法分解结果（极值单调性判据）

由分别采用标准差判据的LCD方法分解结果可以看出，分量ISC1、ISC2和ISC3都分别对应着原信号中调幅调频信号x1（t）、调幅信号x2（t）和正弦信号x3（t），基本上能正确地反映出原始信号的成分特征，这表明了标准差判据（SD＜0.01）和极值单调性判据都可应用于LCD方法。

标准差判据是通过对大量但有限的各种类型仿真信号分解结果的分析而得到的，其阈值也会因自适应时频分析方法的不同而发生变化；极值单调性判据是在对瞬时频率具有物理意义分量的时域形态固有特性研究的基础上得到的，且无需设定任何阈值，具有自适应性。因此，较之标准差判据，极值单调性判据的适用性更强。

现采用极值单调性判据对式（11）所示仿真信号进行EMD方法分解，分解结果如图10所示。可以看出，EMD方法分解出来的各分量都能正确地反映出原始信号的各成分特征，这说明具有自适应性的极值单调性判据也能够直接适用于EMD方法。

2.3.2 实验信号分析

图10 EMD方法分解结果（极值单调性判据）

实测的轴承为6311型滚动轴承，故障是通过在内圈上激光切割开槽来设置的，槽宽为0.15mm，槽深为0.13mm。振动加速度信号由安装在轴承座上的加速度传感器拾取。实验装置如图11所示。

图11 振动试验装置

图12所示是测得的内圈有凹槽的滚动轴承振动加速度信号的时域波形，实验时采样频率为4096Hz，轴转频为20Hz。经计算，滚动轴承内圈故障特征频率为fi＝99.2Hz。

图12 内圈故障滚动轴承振动加速度信号

限于篇幅，本文仅采用极值单调性判据对该实验信号进行LCD方法分解。由于滚动轴承信号的故障信息主要集中在高频段，因此只选取分解结果的前两个ISC分量，如图13所示。

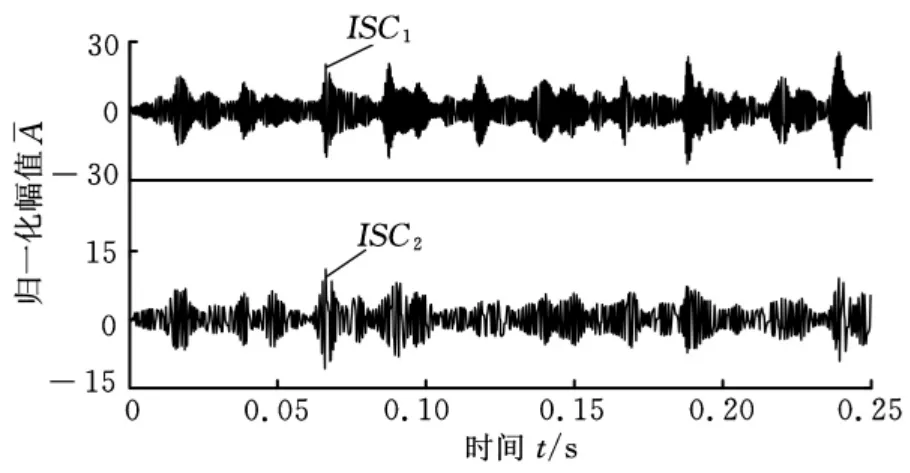
图13 LCD方法分解结果的前两个分量

采用基于Hilbert变换的包络解调方法分别对ISC1、ISC2进行解调，再进行包络谱分析，得到谱图，见图14、图15。可以看出，内圈故障特征频率99.2Hz处都存在着明显的谱线，由此可说明极值单调性判据的有效性。

图14 ISC1的包络谱图

图15 ISC2的包络谱图

3 LCD和EMD的对比分析

限于篇幅，本文仅从计算效率方面对LCD和EMD方法进行初步对比。由于标准差判据阈值会因自适应时频分析方法算法的不同而变化，因此选择适用性更强的极值单调性判据作为LCD和EMD方法分解的分量判据，分别对式（11）所示仿真信号进行分解。LCD和EMD方法分解的结果分别如图9、图10所示，其中各个分量的迭代次数以及分解所需的总时间如表2所示。

表2 LCD和EMD方法分解的迭代次数和分解总时间

由表2可看出，LCD方法的迭代总次数和分解总时间都要少于EMD方法。一方面，EMD方法的基线信号只是通过信号上下极值点包络线的平均来获取，并没有充分利用原始信号数据，而LCD方法利用原始信号本身进行分段线性变换来得到基线信号，较之EMD方法能更加有效地获取原始信号的内在本质特征，这就有利于减少迭代次数。另一方面，EMD方法中采用三次样条插值计算基线信号，计算量较大，而LCD方法采用简单的线性变换，避免了整体插值的过程，这样计算量大大减少。综合以上两方面，LCD方法在计算效率方面要优于EMD方法。

4 结语

LCD方法是一种新的基于极值点的局部特征尺度参数的自适应、非平稳信号处理方法，该方法以信号任意两个相邻的极值点为跨度，并以分段的形式对信号进行线性变换来构造基线信号，从而通过多次迭代将信号自适应地分解为若干个ISC分量之和。本文在提出LCD方法的基础上也在理论方面对其进行了初步探讨，主要做了如下工作：

（1）将EMD方法中的标准差判据应用于LCD方法，并通过大量数据试验确定适用于LCD方法的阈值，对仿真信号的分析结果表明这种判据可以应用于LCD方法。值得指出的是，对于不同的自适应时频分析方法，标准差判据的适用阈值也不同，因此它不具备自适应性。

（2）在对瞬时频率具有物理意义的典型信号的时域形态进行研究的基础上提出了一种新的分量判据——极值单调性判据，仿真和实验信号的分析结果验证了该判据的有效性。较之标准差判据，极值单调性判据无需设定阈值，因此具有自适应性，其适用性更强，也可直接应用于EMD方法。

（3）对比分析了LCD和EMD方法的计算效率，对仿真信号的分析结果表明LCD方法在计算效率方面要优于EMD方法。LCD方法采用对原始信号进行简单的分段线性变换获取基线信号，迭代次数少，计算量小。

LCD方法的提出为自适应时频分析方法提供了一条新的思路，但还有一些理论问题需要研究和完善，例如端点效应、模态混淆以及LCD方法适用的信号范围等。随着这些问题的深入研究，相信LCD方法能够得到广泛的应用。

［1］Huang N E，Shen Z，Long S R.The Empirical Mode Decomposition and the Hilbert Spectrum for Nonlinear and Non－stationary Time Series Analysis［J］.Proceedings of the Royal Society，A，1998，454：903－995.

［2］Huang N E，Shen Z，Long S R.A New View of Nonlinear Water Waves：the Hilbert Spectrum［J］.Annu.Rev.Fluid Mech.，1999，31：417－457.

［3］Frei G M，Osorio I.Intrinsic Time－scale Decomposition：Time－freqeucny－energy Analysis and Real－time Filtering of Non－stationary Signals［J］.Proceedings of the Royal Society，A，2007，463：321－342.

［4］Huang N E，Wu M L C，Long S R，et al.A Confidence Iimit for the Empirical Mode Decomposition and Hilbert Spectral Analysis［J］.Proceedings of the Royal Society，A，2003，459：2317－2345.

［5］Rilling G，Flandrin P，Goncalves P.On EmpiricalMode Decomposition and Its Algorithms［C］／／IEEEEURASIP.Proceedings of IEEE－EURASIP Workshop on Nonlinear Signal and Image Processing（NSIP－03）.Grado，Italy：IEEE，2003：8－11.

［6］程军圣，于德介，杨宇.经典模态分解方法中内禀模态函数判据问题研究［J］.中国机械工程，2004，15（20）：1861－1864.Cheng Junsheng，Yu Dejie，Yang Yu.Research on the Intrinsic Mode Function Criterion in EMD Method［J］.China Mechanical Engineering，2004，15（20）：1861－1864.

［7］Qin S R，Zhong Y M.A New Envelope Algorithm of Hilbert－ Huang Transform［J］.Mechanical Systems and Signal Processing，2006，20（8）：1941－1952.