对锥形扩散器内紊流的数值仿真与分析

肖 瑞

(惠州学院 电子科学系，广东 惠州 516007)

工程技术中，通常利用机械装置与管路系统将流体所具有的速度能转化为压力能，为了减少压力能的损失，常常将扩散器与异径管路联接从而达到压力恢复的效果［1］。作为压力恢复装置的锥形扩散器在科学技术和工程应用中起着重要作用。国际上，研究者们对锥形扩散器内部的紊流进行了大量的实验研究和理论研究。本文采用DLR型k－ε紊流模型·BFC法对整个锥形扩散器内的紊流进行了数值仿真，其紊流场如图1所示。

1 数值仿真模型的基本方程组

仿真对象为轴对称的锥形扩散器内粘性紊流场［2］，其扩散角为 4°，扩散度为 4。由于锥形扩散器内的紊流场，流道断面渐变，数值化边界条件较难处理，考虑到扩散器的轴对称性，在不影响精度的前提下，假定流体为各向同性的不可压缩粘性无旋流，且忽略重力的影响，速度用入口速度U0，坐标用前接管直径D0，紊流动能用，紊流耗散率用0，压力用，时间用D0/U0分别无量纲化，则在圆柱坐标系下，无量纲化的DLR型k－ε紊流模型的基本方程组为［3］:

图1 锥形扩散器内紊流流场模型

方程(5)和(6)中，f2和fμ分别为:

基本方程组中:x，r分别为轴向距离和离开轴心的径向距离;y+为离开壁面的无量纲化距离分别为时均速度分量;k，ε分别表示紊流动能和动能耗散率;v为运动粘性系数且v=1.59×10－5m2/s;vt为涡动粘性系数;Re为雷诺数且Re=U0D0/v;Rt为紊流雷诺数且Rt=k2/vε;f2和fμ为模型函数;Cμ，C1，C2，σ1和 σ2为模型常数。

2 数值仿真的计算条件和算例

本文用DLR型k－ε紊流模型·BFC法对锥形扩散器内的紊流进行了数值仿真，数值仿真的计算条件和算例分别如表1和表2所示:

表1 数值仿真的计算条件

表2 数值仿真的算例

3 数值仿真的结果与分析

锥形扩散器内的紊流具有复杂的压力梯度，在很靠近壁面的紊流流动中，由于流体粘性的影响使得在壁面(尤其是粘性底层)附近，紊流诸量沿y方向急剧变化，一方面紊流脉动由于壁面约束而下降，另一方面分子粘性的扩散作用逐渐增强，流动情况及其复杂。本文主要以流动参数u和k为研究和分析的对象，对两种雷诺数下不同计算条件的四种算例进行数值仿真，并将仿真结果分别与Okwuobi和Singh的实验数据［6－7］进行比较，分析不同计算条件对和k的影响。

3.1 模型函数组的影响

其它计算条件不变，改变模型函数f2和fμ，则不同的模型函数组对时均速度和紊流动能k的影响分别如图2和图3所示。由图可知，算例A－1和A－2的数值仿真结果和k均与实验数据符合较好，图2中，沿主流动方向，越靠近渐扩管出口(x/D0=7.1)，数值仿真结果与实验结果符合越好。在靠近渐扩管壁面处，算例A－1比算例A－2的数值仿真结果更接近于实验结果，但在渐扩管轴心处，算例A－2比算例A－1的数值仿真结果更接近于实验结果。图3中，模型函数组的改变对k的影响稍大，在动能k到达峰值之前，算例A－1与实验结果符合较好，随着动能K的不断减小，算例A－2与实验结果的符合程度较好，并且离渐扩管入口越远，算例A－1和A－2与实验数据符合越好，模型函数组的改变对k的影响越小。

图2 的仿真结果与实验结果的比较(模型函数组的影响)

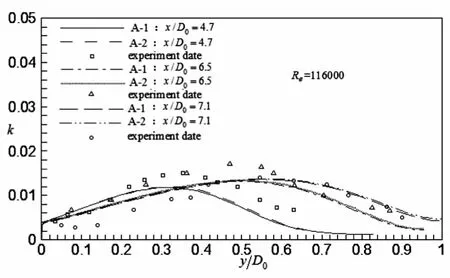
图3 k的仿真结果与实验结果的比较(模型函数组的影响)

3.2 模型常数组的影响

其它计算条件不变，选择不同的C1，则不同的模型常数组Cμ，σ1，σ2，C1和C2对时均速度和紊流动能k的影响分别如图4和图5所示。由图可知，模型常数组的改变对和k的影响较大，但没改变和k的布规律，总体来说，算例A－1比算例B－1的数值仿真结果稍好。图4中，C1越小，在渐扩管轴心处的时均速度越大，但达到峰值时离开壁面的距离越小，且越靠近渐扩管出口(x/D0=7.1)，算例B－1的数值仿真结果与实验结果相差越大。图5中，算例B－1的数值仿真结果与实验结果相差较大，C1越小，紊流动能k越小，k达到峰值时离开壁面的距离也越小;在渐扩管轴心处，三个断面算例B－1的k值均小于算例A－1的k值，且在轴心处趋于一致。

图4 的仿真结果与实验结果的比较(模型常数组的影响)

图5 k的仿真结果与实验结果的比较(模型常数组的影响)

3.3 时间步长的影响

其它计算条件不变，选择不同的时间步长△t，则时间步长△t的改变对时均速度和紊流动能k的影响分别如图6和图7所示。由图可知，时间步长的改变对和k几乎没有影响，不仅没改变和k的分布规律，并且算例A－2和B－2的数值仿真结果几乎一致，均与实验结果符合较好。为了更好地说明这一点，下面列举出两种算例下代表性断面和k的数值仿真结果，如表3和表4所示。

图6 u的仿真结果与实验数据的比较(时间步长的影响)

图7 k的仿真结果与实验数据的比较(时间步长的影响)

表3 不同时间步长下数值仿真结果的比较(断面x/D0=4.7)

表4 不同时间步长下数值仿真结果的比较(断面x/D0=5.9)

由表3和表4可知，时均速度和紊流动能k在不同时间步长下的数值仿真结果最大偏差为0.001和0.00001，可见改变时间步长△t对和k的数值仿真结果影响极小。经多次仿真发现，应当注意的是，时间步长△t不能取得太大，当时间步长取0.0015时，数据不再收敛，并且当限定小循环的迭代次数I=20时，将时间步长取为0.001较为合适。

4 结论

本文用DLR型k－ε紊流模型·BFC法对扩散角为4°，扩散度为4的锥形扩散器内充分发展的不可压缩粘性紊流进行了数值仿真。通过对两种雷诺数下四种算例的仿真结果与实验结果的比较发现:算例A－1，A－2，B－2均与实验数据符合较好，预测精度较高;沿主流动方向，越靠近渐扩管出口，模型函数组的改变对和k的影响越大;改变模型常数组对和k的影响较为显著，但不改变和k的分布规律，模型常数C1值越小，在渐扩管轴心处的时均速度越大，但达到峰值时离开壁面的距离越小，对于紊流动能k，C1越小，紊流动能k越小，k达到峰值时离开壁面的距离也越小;时间步长的改变对和k几乎没有影响。

总之，本研究得到了较为精确的数值仿真结果，丰富了带有前接管的锥形扩散器管内紊流的计算机仿真诊断系统，为紊流科学研究和工程应用提供可靠的数据，有利于机械、矿山、石油开采以及国防等工程的实际应用。

［1］何永森，舒适，蒋光标，肖映雄．管路内流体数值计算与仿真［M］．湘潭:湘潭大学出版社，2011，8．

［2］肖瑞．锥形渐扩管内逆压梯度紊流场的数值仿真［J］．广西科学，2009，16(2):120－123．

［3］肖瑞，何永森．对锥形渐扩管内紊流近壁特性的研究［J］．惠州学院学报(自然科学版)，2009，29(3):5－9．

［4］将光彪，何永森，舒适，等．用DHR模型与AMG法对渐扩管内紊流数值仿真［J］．矿业研究与开发2009，29(3):47－50．

［5］ROUSSEAU A N，ALLBRIGHT L D，TORRANCE K E．A Short Comparison of Damping Functions of Standard Low －Reynolds－Number Models［J］．JUNE 1997，460．

［6］OKWUOBI P A C，AZAD R S．Turbulence in a Conical Diffuser with Fully Developed Flow at Entry［J］．J Fluid Mech，1973，57(3):603

［7］SINGH D，AZAD R S．Turbulent Kinetic Energy Balance in a Conical Diffuser［M］．Proc of Turbulence，1981:21．