基于EM算法的改进MLM模型及参数估计

闵素芹，何晓群

（1．中国传媒大学 理学院，北京 100024；2．西京学院 应用统计科学研究中心，陕西 西安 710123）

一、引 言

分层模型（multilevel models，MLM）是针对分层数据发展起来的，它可以对个体水平（微观层）和组水平（宏观层）同时进行分析。分层模型的应用越来越广泛，其参数估计和统计推断方法的研究已较为成熟［1］。

很多问题的研究面临个体和所在区域（组织）两个层面，即个体按不同的地理单元（如：社区、城市、地区等）分组，实证模型需要将微观和宏观数据联合起来。在生物学、气象学和流行病学等研究中，Diggle、Tawn、Moyeed、Zhang、Christensen、Zhu、Gu、Peterson等学者将广义线性混合模型与Kriging方法结合起来，建立了空间广义线性混合模型（SGLMM），对连续空间域的离散型数据，尤其是计数数据进行推断和预测［2－5］。Ancelin提到空间统计和空间计量模型所面临的挑战时指出按一层观测值（如：空间单元层）进行的分析，不能提供低层（如个体行为）有用的信息。而分层建模能够同时顾及微观层和宏观层，将其扩展到处理空间数据有待于进一步研究［6］。

本研究将针对传统分层模型分析以地理单元分层的空间分层数据时存在的问题，将空间统计和空间计量经济模型的思想引入到分层模型中，在传统分层模型的层-2中加入空间参数和空间邻接矩阵来反映空间自相关性。空间效应以空间滞后模型来表达，构建了空间分层线性模型。模型改善了分层模型和空间计量模型处理具有空间自相关效应的分层数据时的不足之处。然后，给出了空间分层模型中固定效应、方差协方差成分和空间回归参数的最大似然估计，在运用期望最大化算法时，空间回归参数没有显式解，故结合运用了Fisher得分算法。

二、考虑空间效应时分层模型的改进

传统两层模型的一般形式为：

在以空间地理单元分组的情况下，组之间会具有空间依赖性（或空间自相关）。这种情况会违反传统模型残差分布的Gauss－Markov假定，残差的空间模式存在空间依赖性，忽视空间效应将造成模型设定的偏差和计量结果的非科学性。针对传统分层模型分析以地理单元分层的空间分层数据时存在的问题，笔者将在分层模型中考虑空间效应，空间效应由空间滞后模型表达。

模型（1）中的R＋1个参数可以看作随机的，也可将其中一个或几个参数视为固定的（即J个组都相同）。因此，可将层-1模型表达成如下形式：

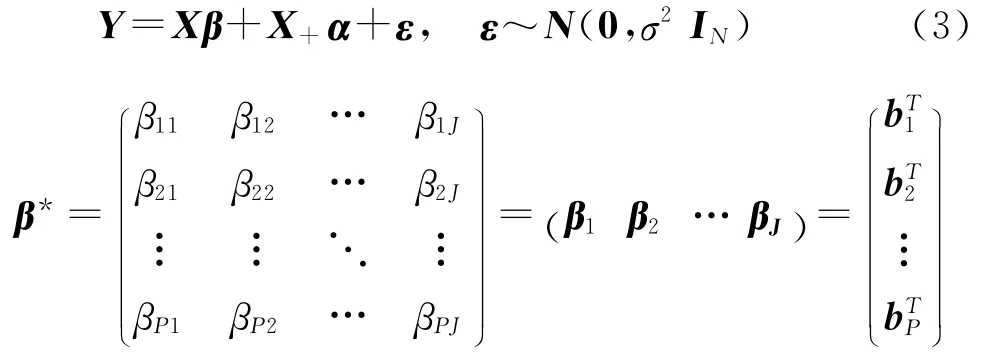
其中，bk＝ （ βk1 βk1… βk1，k＝1，2，…，P，Z＊是J×（F＋1）的自变量矩阵，γk是（F＋1）×1的固定效应向量，ζk是J×1的层-2误差向量，或称随机效应向量。

β是PJ×1的列向量，是β＊的堆栈，是按组排列的，依次为第1个地区的P个参数，第2个地区的P个参数，…，第J个地区的P个参数。即：β＝（β11，β21，…，βP1，β12，β22，…，βP2，…，β1J，β2J，…，βPJ）T。其中，第2个下标表示地区。而bk＝（βk1 βk2… βkJ），k＝1，2，…，P。即第k个解释变量系数的J个值。所以，层-2表达成矩阵形式

其中β＝vec（β＊），βij表示第i个解释变量的系数（或截距项）在第j个地区的值；βj表示第j个地区的P个参数；bTk表示第k个解释变量的系数（或截距项）在1，2，…，J组的值。

在传统的层-2模型中引入空间参数和空间邻接矩阵来反映空间自相关性，空间效应以空间滞后模型来表达：时，βij的排列顺序要调整成与β相同。

层-2模型（4）的矩阵表达形式为：

层-2模型（5）可以写成：

将式（6）代入式（3），可得到混合模型：

模型中ε～N（0，σ2IN），β为随机参数向量，它由本地区的自变量和邻近地区的β向量来解释。R＝di-ag（ρ1，ρ2，…，ρP），在层-2模型中ρ1，ρ2，…，ρP分别对应β中的P个参数。

三、改进MLM模型实例分析

下面给出一个实例，旨在直观的说明改进后模型的形式、思想及其研究的必要性。

郭志刚运用分层模型很好的研究了宏观的社会经济环境与微观的妇女个人特征如何影响二孩生育间隔［7］。笔者借鉴该研究，将其扩展到空间自相关的数据来阐述新模型的应用。

假设研究某省的农村二孩生育间隔，该省共J个县，在每个县抽取一定样本量（nj）的育龄妇女进行问卷调查，这样得到的数据就包含个人信息和县级的宏观层数据，育龄妇女嵌套于县。

首先建立个人层次各解释变量对二孩生育间隔的影响的层-1模型：

其中，各变量都进行组均值中心化处理，β0j是层－1模型的截距，表示第j个县的平均二孩生育间隔，j＝1，2，…，J；i＝1，2，…，nj，nj是第j个县的样本容量；下标ij表示第j个县中的第i个育龄妇女。

考虑到所在县的经济、社会、文化氛围等会作用到育龄妇女身上，进而影响育龄妇女的生育间隔，所以各县育龄妇女的生育间隔的总体情况会有所不同。反映到模型中，即允许每个县有不同的截距，β0＝（β01，β02，…β0J）T，β0j表示第j个县的平均生育间隔，j＝1，2，…，J。该县的平均二孩生育间隔会受到该县的经济发展水平、总体受教育程度等因素的影响。

同时，由于相邻的县有共同的历史、社会、经济、文化背景，其运输、信息等成本比较低，各种往来比较频繁，教育状况、健康情况、人们的观念等都具有相似性。在地理空间上表现为一种集群现象，具有空间依赖性，即第j个县的平均生育间隔会受到邻近县平均生育间隔的影响，忽视空间效应将造成模型设定的偏差。

因此，在层-2模型中既要考虑本县的经济发展水平和教育水平对该县平均二孩生育间隔的影响，也要考虑邻近县的影响。

当存在空间依赖性时，建立县级层次的各解释变量和空间自相关性对层-1截距项的影响的层-2模型：

其中，ρ是空间自回归系数，ξ是误差项向量，Wβ0是空间滞后项。模型中，所研究县的平均生育间隔不仅与本县的经济发展水平和平均受教育程度有关，还与相邻县的平均生育间隔有关。

综上，改进后的分层模型的混合模型矩阵表达形式为：

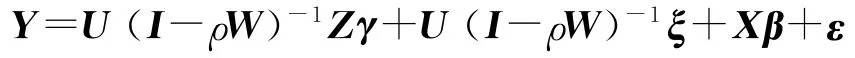
其中，Y＝（二孩间隔ij）N×1，

四、基于EM算法和Fisher得分的最大似然估计

在进行最大似然估计时，完整数据是Y，X，X＋，W，ξ，观测数据是Y，X，X＋，W，α，σ2，需要被估计的参数是R，γ，T。

（一）最大化步（M Step）

给定X，β，X＋，α，σ2，可得Y 的条件分布为：

Y｜X，β，X＋，α，σ2～N（Xβ＋X＋α，σ2IN） （8）

当给定X，β，X＋，α，σ2，R，W，Z，γ，T 时，Y 的条件分布为：

根据多元正态分布剖分定理可得：

计算可得添加后验分布的对数似然为：

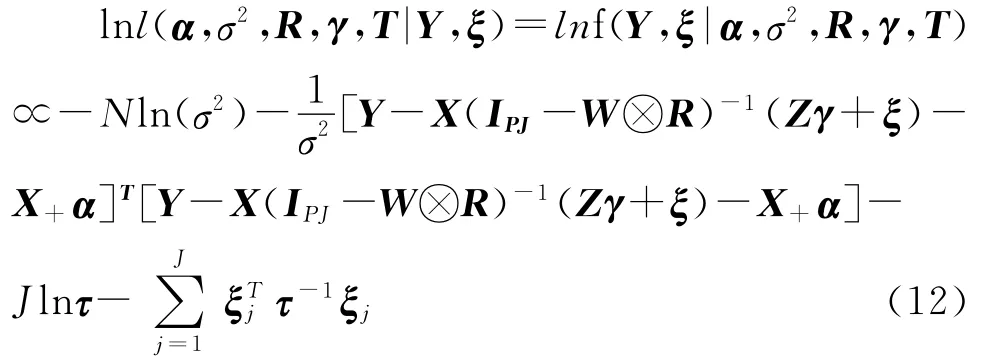
式（12）对数似然函数分别对α，σ2，R，γ，τ求偏微可得：

（二）期望步（E Step）

由式（10），根据正态分布剖分定理［8］59－60，

（三）EM 算法

1．给出初始值α（0），σ2（0），R（0），γ（0），T（0）；设第k＋1次迭代开始时的参数估计值为α（k），σ2（k），R（k），γ（k），T（k）。

2．估计完整数据的充分统计量：E（ξ｜Y，α，σ2，R，γ，T），E（ξξT｜Y，α，σ2，R，γ，T），E（ξTξ｜Y，α，σ2，R，γ，T），这些期望值根据前一步迭代得到的α（k），σ2（k），R（k），γ（k），T（k）值求得。

3．由式（13）计算τ（k＋1），由式（14）计算s1，由式（15）计 算 E （ H1） ，利 用 （＾σ2）（k＋1）＝ （ σ2）（k）－（E（H1））－1s1得 到 新 的 参 数 估 计值 （＾σ2）（k＋1），由 式（16）计算s2，式（17）计算E（H2），利用

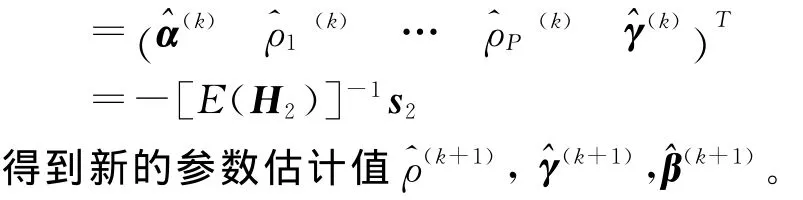
4．将新的参数估计值代入到步骤2中，重复上述步骤，M步和E步不断地迭代交互运算，直到所估计的参数值都很接近，或每次迭代运算的对数似然函数值变化很小，就达到收敛。可以通过计算每一步迭代的对数似然值来加以监测。

五、结束语

学者们近年来对空间经济和区域科学有较多的关注。很多问题的研究面临个体和所在区域（组织）两个层面，即个体按不同的地理单元（如：社区、城市、地区等）分组，实证模型需要将微观和宏观数据联合起来。因此，需要将分层模型和空间计量模型纳入同一体系进行研究，如何进行结合是一个难点。针对这种情况，本研究提出了改进的分层模型，模型同时考虑了数据的嵌套结构和地理单元之间的空间依赖性。模型有四种参数的估计，包括固定效应、随机的层-1系数、方差协方差成分、以及空间回归参数，每一种参数的估计都依赖于其他的参数。而表达空间效应的空间回归参数ρ增加了估计的难度，因为在令对数似然函数关于ρ的偏微分等于零时，ρ没有显式解。本研究在运用EM算法时，结合运用了Fisher得分算法，给出了最大似然估计的期望最大化算法。

［1］ 何晓群，闵素芹．分层线性模型层-1自变量中心化问题的研究综述［J］．统计与信息论坛，2009，24（9）．

［2］ Diggle P J，Tawn J A，Moyeed R A．Model－Based Geostatistics［J］．Journal of the Royal Statistical Society，Series C，1998，47（3）．

［3］ Zhang H．On Estimation and Prediction For Spatial Generalized Linear Mixed Models［J］．Biometrics，2002，58（1）．

［4］ Christensen O F，Roberts G O，Skld M．Robust MCMC Methods For Spatial GLMM’s［J］．Journal of Graphical and Computational Statistics，2006，15（1）．

［5］ Zhu H，Gu M，Peterson B．Maximum Likelihood from Spatial Random Effects Models Via the Stochastic Approximation Expectation Maximization Algorithm［J］．Statistics and Computing，2007，17（2）．

［6］ Anselin L．The Future of Spatial Analysis in the Social Sciences［J］．Geographic Information Sciences，1999，5（2）．

［7］ 郭志刚，李剑钊．农村二孩生育间隔的分层模型研究［J］．人口研究，2006（4）．

［8］ 张尧庭，方开泰．多元统计分析引论［M］．北京：科学出版社，2003．