基于CORDIC的基4－IFFT/FFT算法的硬件实现

王玉华，温 浩，任宏亮，覃亚丽

(浙江工业大学信息学院，浙江杭州310023)

0 引言

快速傅立叶变换是正交频分复用(Orthogonal Frequency Division Multiplexing，OFDM)技术中重要的数字信号处理方式。在可见光通信中［1］，当传输速率在100Mb/s以下时码间干扰对通信系统的性能影响不大，当速度更高时，利用OFDM可减少码间干扰的优势，将本文给出的算法应用于可见光OFDM调制系统中，既能实现高速传输，又能大大降低成本。近几年来，人们不断地对坐标旋转数字计算机(Coordinated Rotation Digital Computer，CORDIC)算法进行探索研究，并提出了相应的算法和方案以适应不同的需求［2］。FFT有基－2，基－4，基－8等多种算法，基数越高，总运算量就越少。但基数越大，实现起来也越复杂。Cyclone II系列器件的成本比第一代Cyclone器件低30%，逻辑容量大了3倍多，可满足低成本大批量应用需求。为避免使用乘法器，简化结构，减少处理器内核面积，可采用CORDIC算法实现基4－FFT算法。

1 基4－FFT与CORDIC算法的基本原理

基4－FFT的基本原理如下:设x(n)为N点有限长序列，其DFT为:

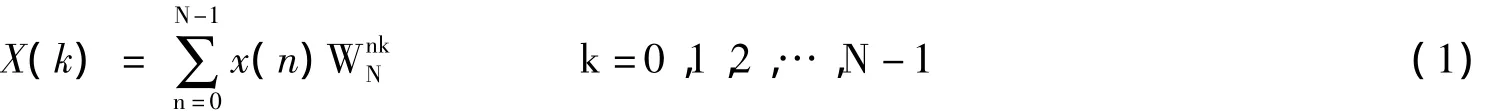
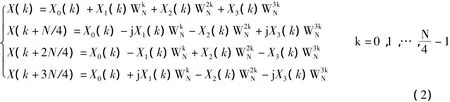
从式2可以看出一个4点组合迭代需要进行3次复数乘法和8次复数加减法运算，与传统的基2－FFT算法比较，整个基4－FFT过程中的乘法次数减少了25%。

CORDIC算法的基本原理是:设数据与旋转因子相乘的表达式为:Xk=X0，其中设X0=x0+jy0，Xk=xk+jyk，将旋转因子代入，令θ=－2 kn/N，结合欧拉公式可得Xk的实部和虚部分别如下式所示，复数序列和旋转因子相乘可看作是将向量X0旋转了θ角度，假设初始向量经过N次旋转后得到新向量，且每次旋转角度δ为2的倍数，则:

第i次旋转角度为δ(i)=arctan(2－i)，当旋转次数一定时会趋于一个常数。从式3也可看出，对于角度θ，只需要硬件加减法和移位器就可得出结果，其中移位器用来实现乘法和除法，从而减少硬件资源。

2 蝶形运算器的结构设计

FFT蝶形单元硬件实现主要有4种方式:递归结构、级联结构、并行结构和阵列结构。本文采用了递归结构的蝶形运算，以1个基4蝶形运算单元为基本结构，每一级运算按递归方式进行。蝶形运算单元一直出于忙碌状态，直至运算结束。递归结构的主要优点就是硬件占用资源少，结构简单，从而使其控制逻辑单元的设计更加清晰明了，处理器的稳定性较高。

基4－蝶形运算结构如图1所示。蝶形运算中每一级输出的结果分别经地址产生器到实部和虚部存储器并按递归方式输入基4运算模块进行下一级的运算。FFT或IFFT运算的选择，取决于标志信号的值，它为0，则进行FFT运算;它为1，则进行IFFT运算。

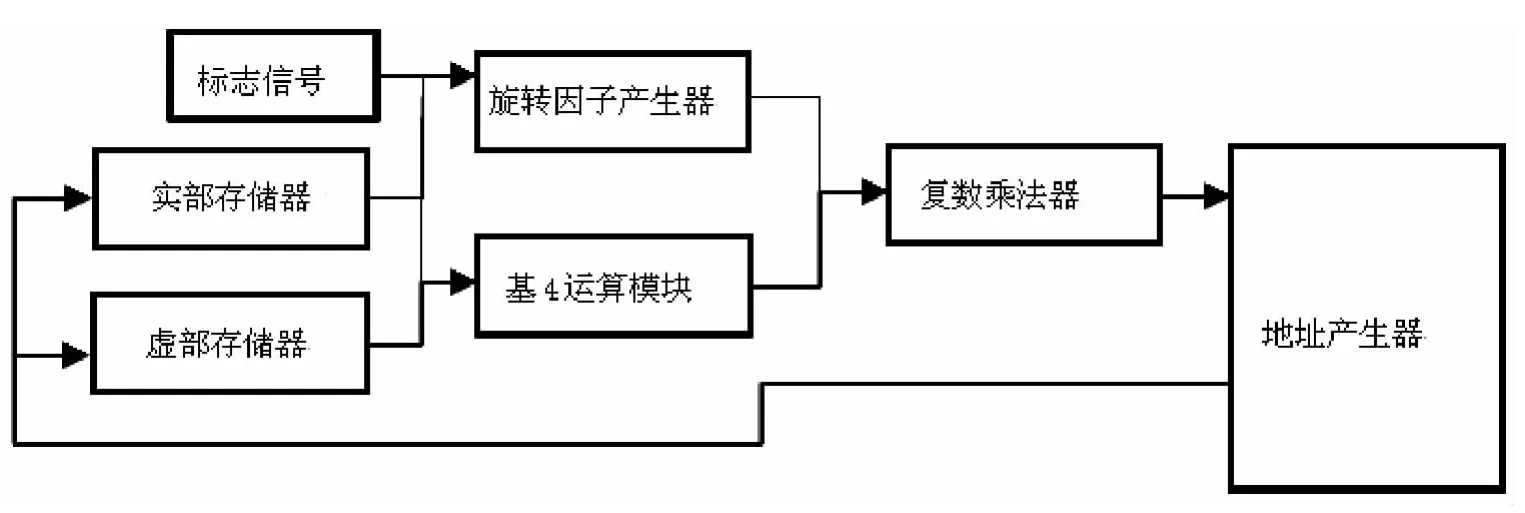
图1 基4－蝶形运算结构

复数乘法器模块将基4运算模块中产生的数据与旋转因子相乘，为避免使用乘法器，采用流水线结构的CORDIC算法，只需移位和加减法即可实现乘法。由式δ(i)=arctan(2－i)看出知道旋转次数i，就可知道旋转度数。所以在编码中设置了一个arctangent函数，它的功能是根据旋转次数i，返回一个20bit的arctangent值。预先把旋转次数与对应返回值arctangent放入表中［7］，加快了运算速度。通过计算发现当i大于17时，输出结果基本为0，即与起始值重合。

3 仿真结果及硬件实现

本文选用Altera公司生产的Cyclone II系列芯片进行验证，时钟频率50MHz，FFT点数为1 024。在VHDL语言中只能输入整数，而FFT处理过程中会出现小数，所以将12位的处理序列按定点运算的方式表示，前4位为有效的整数位，后8位为小数位。同样，14位的输出序列中高2位为符号位，后12位定义同输入。根据如下判断准则:当输出序列的符号位为“00”时，若输出整数位=输入整数位，则说明结果正确;若当输出序列的符号位为“11”时，若输出整数位+1=输入整数位，则说明结果正确，反之有误。小数位可忽略。如此准确地实现数据的发送与接收。

为实现OFDM信号的实数化，方便应用于可见光OFDM调制解调系统中，令输入序列满足Hermi-tian对称，即x(N－m)=x(m)*，其中N=1 024为FFT点数。经多组数据的反复验证，证实本文给出算法的正确性。为方便截图，将二进制序列用带符号的整数表示，例如100000000000表示为－2048。分别在位置 1，93，96，99，101，104，108，111，913，916，920，923，925，928，931 的位置按 Hermitian 对称的规律，输入(实部)/(虚部):－2048/0，0/256，0/512，0/768，0/1024，0/1280，0/1536，0/1792，0/－1792，0/－1536，0/－1280，0/－1024，0/－768，0/－512，0/－256，仿真结果如图2 所示，指定位置输出数据的放大图如图3、4所示。

图2 1 024点FFT的输出结果

图3 第92至110位置上的输出值

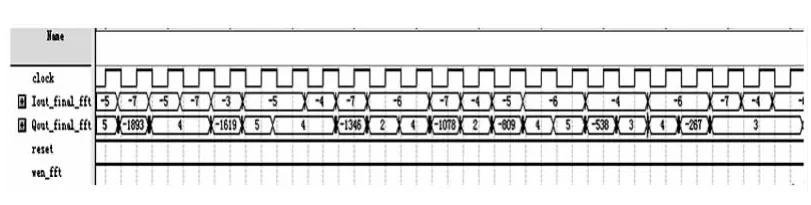
图4 第912至933位置上的输出值

为了便于分析，分别将输入序列的整数位与输出序列的符号位与整数位整理如表1所示。从划线部分可以看出，根据判断准则，输出序列与输入序列完全一致。

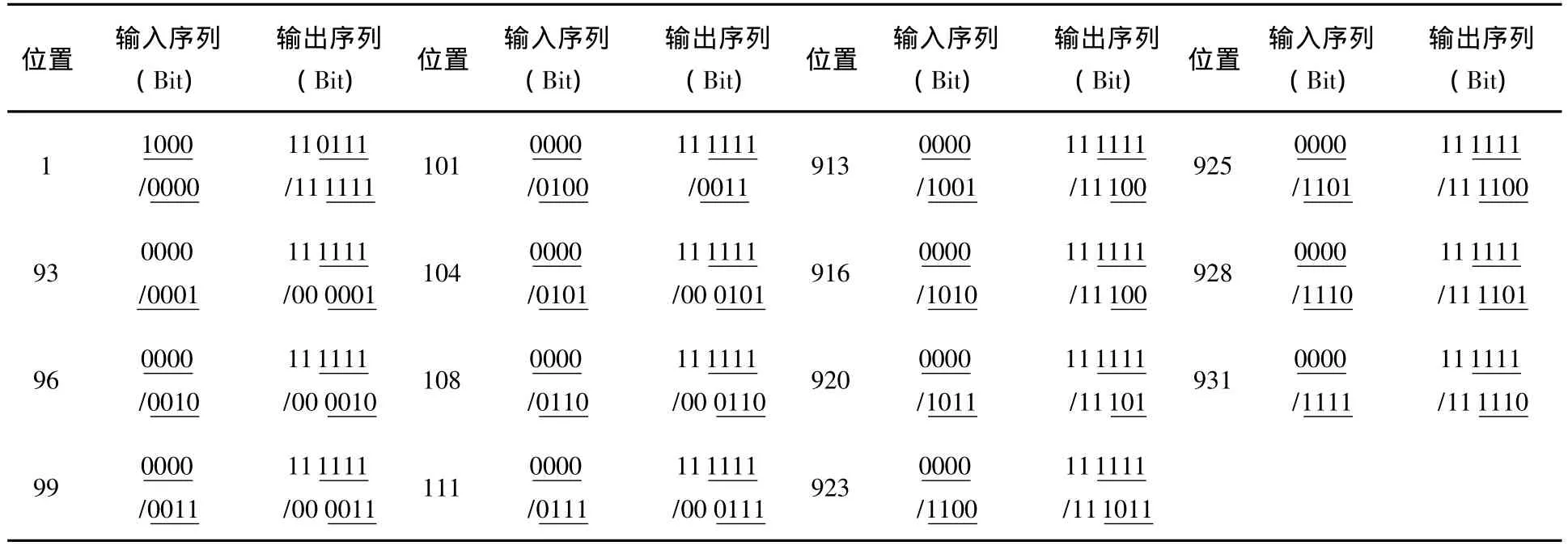
表1 输入/输出序列整数位比较表

在验证算法正确的基础上单独仿真基于CORDIC的基4－FFT算法，编译结果如图5所示，硬件连接图如图6所示。

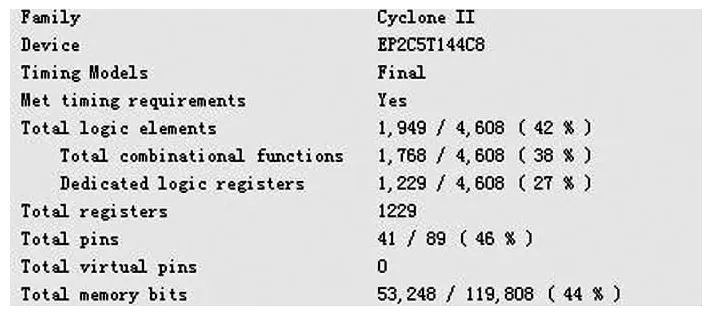
图5 时序仿真编译报告

图6 硬件实现连接图

从时序仿真结果中可以看出，本文给出的算法只用了1 949个逻辑块，1 229个专用寄存器，0个乘法器，这不仅体现了CORDIC算法可避免使用乘法器的优点，而且相比于文献［4］中1 024点级联结构的FFT处理消耗了4 399个逻辑单元，本算法使用的逻辑块单元减少了55%。对于64点的FFT运算，在20MHz时钟频率下，本文给出的算法运行时间如图7所示，约为13μs，与文献5中流水线结构的处理消耗时间 12μs相比，仅慢了1μs，同样可达较高的速度［5］。

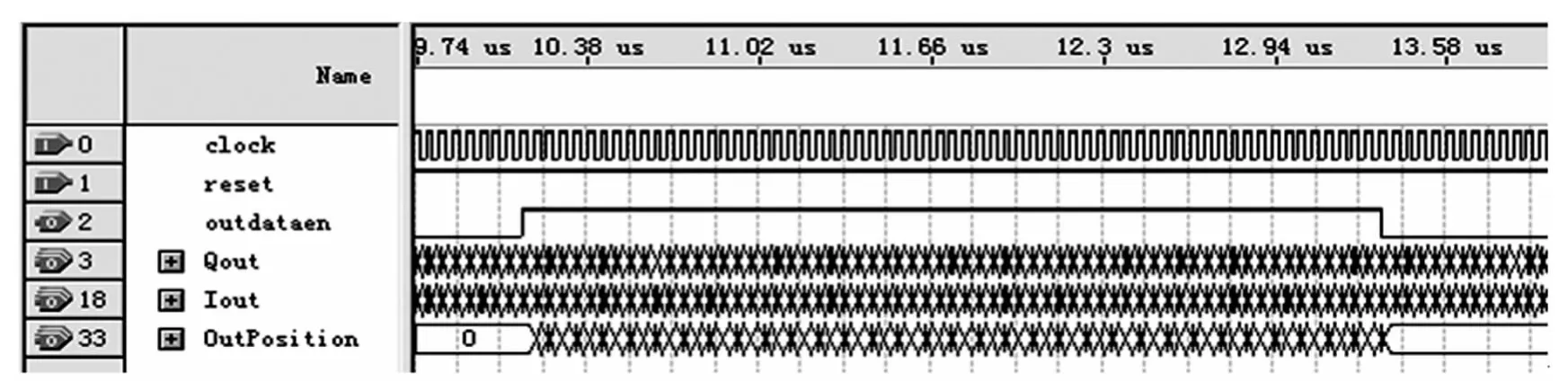
图7 64点－FFT波形仿真图

4 结束语

本文给出了基于CORDIC的基4－IFFT/FFT算法，结果表明，该算法对于1 024点FFT运算只需1 949个逻辑块和1 229个寄存器，较级联结构的处理器省55%的硬件资源。对于64点FFT运算与流水线结构的处理器相比，速度依然较快。整个系统递归结构、CORDIC算法、查表法找旋转因子的设计应用大大节省了硬件资源，又采用模块化思想设计，可移植性强，通用好，稍作改动，可实现不同精度和FFT点数的运算。很适用于可见光OFDM调制解调系统。

［1］Shinichiro Haruyama.Visible light communication using sustainable LED lights［C］.Geneva:International Telecommunication Union，2013:100 －106.

［2］鞠建波，杜爱国.基于CORDIC算法的QDDS的FPGA实现及精度分析［J］.电视技术，2007，47(1):112－116.

［3］郑君里，应启珩，杨为理.信号与系统(第2版)［M］.北京:高等教育出版社，2000，136－137.

［4］张竺军，钱建平.基于FPGA的级联结构FFT处理器的优化设计［J］.计算机应用技术，2009，26(22):141－143.

［5］蒋斌，黄华灿.64 点 FFT/IFFT 的 FPGA 实现［J］.电子技术，2008，8(4):37－39.