在FPGA上实现FFT的高效串行流水线结构
朱永前 李 霄
(南京长峰航天电子科技有限公司 南京 211800)
0 引言
快速傅里叶变换(FFT)是信号处理领域最重要的算法之一,信号的时频域转换、信号与特征卷积、信道化等都需要FFT算法[1]。高效的FFT实现方法能降低信号处理资源占用及提升运算速度,在卷积计算中,为了使参与卷积的特征向量足够长,往往需要大点数FFT[2]。FPGA中数据并行FFT实现方式资源消耗非常大,无法做到较大点数,本文介绍频域切分基4-FFT算法的一种串行实现方法,资源消耗少,FFT点数可变,通过巧妙设计每级蝶形变换省去码位倒置排序,是一种高效串行流水线结构。下文以4096点FFT为例,其它4的次幂点FFT同样适用,FFT点数为2的次幂非4的次幂时,只需最后一级蝶形变换用基2变换,无本质差异,文中不再赘述。
1 基4-FFT算法
数字信号x的离散傅里叶变换[3]X定义为:
按基4频域切分推导FFT算法如式(1)所示。
(1)
如公式(1),N点傅里叶变换经蝶形变换拆分成4组N/4点傅里叶变换,且N/4点傅里叶变换结果按模4取余放置即为N点傅里叶变换的结果,如此递推即为基4频域切分FFT。对于4096点FFT,经6级蝶形变换得到最终结果,每级进行1024次蝶形运算。
2 串行结构设计
算法实现整体结构如图1所示,4096点原始数据串行输入,基4拆分后成4路1024点串行数据,再经6级蝶形变换,基4合并后形成4096点FFT结果串行输出。

图1 4096点基4-FFT流水线结构
2.1 基4拆分及合并
根据基4-FFT递推公式(1),基4拆分将数据按时间先后拆分成4路,前1024点为第一路;第1025~2048点为第二路;第2049~3072点为第三路;第3073~4096点为第四路,四路数据对齐后接入蝶形变换。基4合并与基4拆分是完全相反的过程,如图2所示。
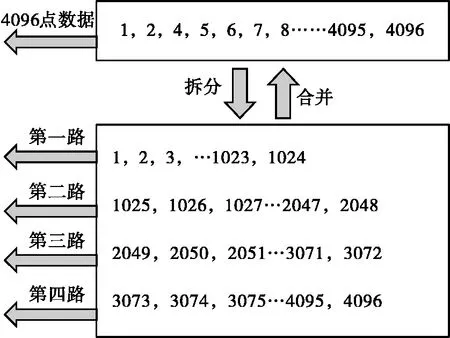
图2 基4拆分及合并示意图
2.2 蝶形变换
蝶形变换分为旋转因子产生模块、蝶形运算单元、串并串转换模块,如图3所示。旋转因子产生模块接收数据序数,返回旋转因子给蝶形运算单元,蝶形运算单元接收数据和旋转因子,进行蝶形运算后将数据接入串并串转换模块,转成下一级蝶形变换需要的数据序列后输出。
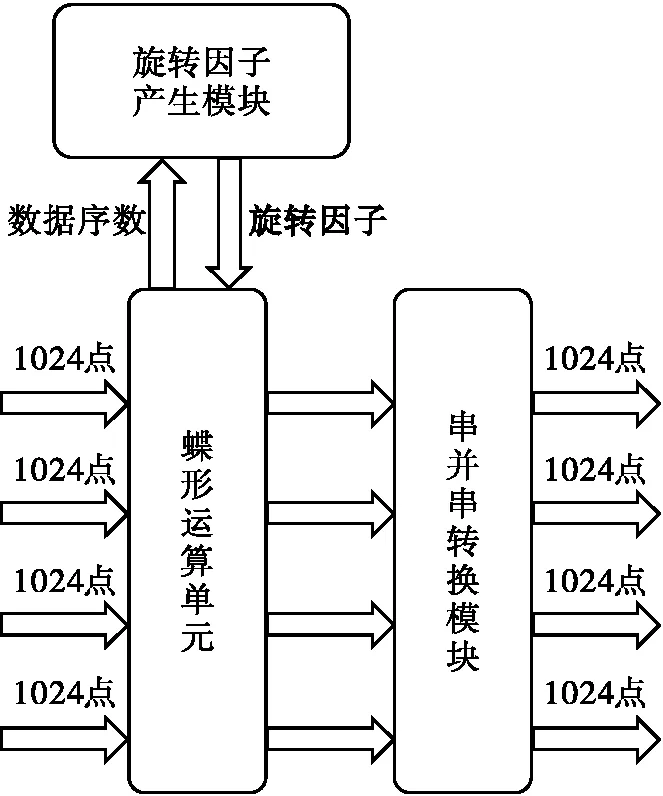
图3 蝶形变换
2.2.1 旋转因子
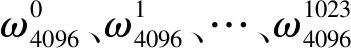
记蝶形变换的级数为S(S从0~5),随着4路1024点数据传入,数据序数k从0递增至1023,记kc

2.2.2 蝶形运算
记x1(k)、x2(k)、x3(k)、x4(k)为4路数据,k从0递增至1023,由公式(1)可知,蝶形运算式为
(2)
每级蝶形变换有1个蝶形运算器,4路数据各1024点串行输入,以流水线形式依次完成1024次蝶形运算。
2.2.3 串并串转换
串并串转换模块的功能是接收蝶形运算后数据,并转成下一级蝶形变换需要的数据序列。该模块是本文方法与其他FFT实现方法[4-6]的核心区别,其他方法将同一路的连续数据块拆分到4路上,而本文方法将同一时刻4路的数据块合并到1路上。
第S级蝶形变换,串并串转换模块4路输入数据,每路以4S个数据为一块,以块为单位,将时间序数据转换为路优先数据,即按数据到来先后优先填充第1路,第1路填充完1024个数据后填充第2路,以此类推完成4路数据的填充,如图4为第1级蝶形变换数据序列调整示意图。为保证4路输出数据时序对齐,需将数据先串转并,再并转串。数据序列调整设计巧妙,所有蝶形变换完成后,无需进行四进制码位倒置输出[7-8]。
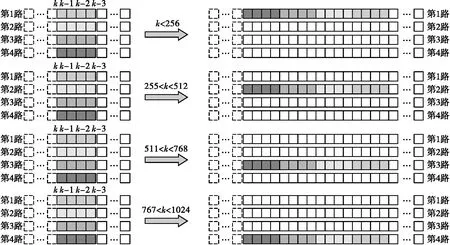
图4 第1级蝶形变换数据序列调整示意图
3 仿真分析
输入信号为频率60MHz脉宽16μs的点频脉冲信号,在Vivado软件中进行仿真,FPGA时钟频率为200MHz,计算结果如图5所示。仿真用时41.14μs,其中基4拆分消耗3072个时钟周期,除最后一级外,每级蝶形变换的串并串转换消耗1024个时钟周期,合计3072+1024×5=8192个时钟周期,200MHz时钟下共40.96μs,其余少量时间为蝶形运算乘法和加法消耗。为验证计算结果的正确性,将Vivada仿真结果与Matlab中直接FFT结果对比,如图6所示,忽略定点运算导致的微小数值精度误差,计算结果完全一致。

图5 FFT仿真结果

图6 FFT结果(绝对值)对比
与码位倒置排序FFT串行实现方法相比,本文方法无需码位倒置排序过程,资源消耗及运算时间都会更少,理论上运算时间少1024个时钟周期,200MHz时钟频率下为5.12μs。在同样的FPGA硬件(xc7vx690tffg1927-2)条件下,在Vivado软件中进行仿真、综合、实现,两者布局布线后的资源占用及计算用时对比如表格1,可见本文方法串并转换设计优于其他方法,且计算时间相差46.26-41.14=5.12μs,与理论分析一致。
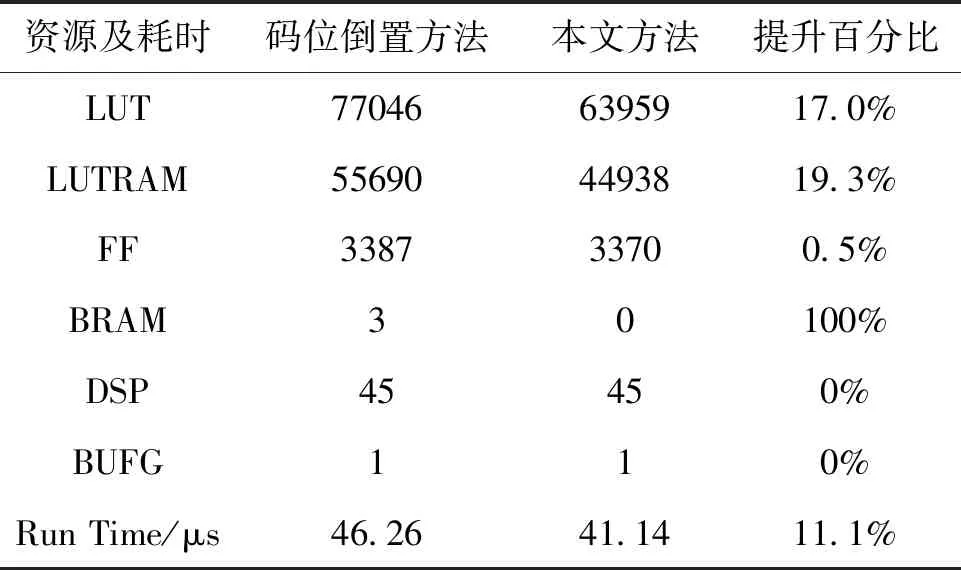
表1 码位倒置方法与本文方法资源及耗时对比
4 结束语
本文提出在FPGA上实现FFT的一种设计方案,推导了频域切分基4-FFT的蝶形变换公式,给出了FFT的串行流水线结构,详细讲解了蝶形变换每个模块的设计思路,通过巧妙设计每级蝶形变换的数据序列,节省了重排序步骤,从而无需码位倒置即可得到自然序的FFT结果。对4096点数据进行了仿真,需要的资源少,耗时短,仿真结果正确。

