一类非对称损失函数下几何分布可靠度Bayes估计

张国林

(宜春学院数学与计算机科学学院，江西宜春 336000)

一类非对称损失函数下几何分布可靠度Bayes估计

张国林

(宜春学院数学与计算机科学学院，江西宜春 336000)

文章在一类非对称损失损失函数下,讨论了几何分布可靠度的Bayes估计问题.在可靠度的先验分布为贝塔共轭先验分布下,得到了可靠度的Bayes估计、多层Bayes估计,最后给出了一个实际应用例子。

可靠度;Bayes估计;多层Bayes估计;几何分布

随着科学技术的进步,产品的可靠性越来越高,导致很多产品的寿命分布具有无记忆性的特点。而几何分布由于其具有无记忆性而成为离散型分布中最为重要的一种分布,除在可靠性和应用概率模型中得到了广泛的应用和研究外,近年来该分布在信息工程、控制论以及经济学中也得到了很大的重视和应用。在贝努里试验中,设R为每次试验成功的概率(可靠度),若进行了x+1次试验,前x次试验成功但第x+1次试验不成功的概率为

则称随机变量X服从几何分布,其中参数R(0＜1＜R)称为可靠度。

本文将在一类非对称损失函数下研究几何分布(1)可靠度的Bayes估计、多层Bayes估计以及E Bayes估计问题。

1 Bayes估计

基于过去的经验或者以往试验数据,我们可以得到关于参数的一些先验知识,而这些先验知识通常用参数的先验概率密度函数来表示。对于几何分布最常用的先验分布为其共轭先验分布-贝塔先验分布Beta(a,b)：

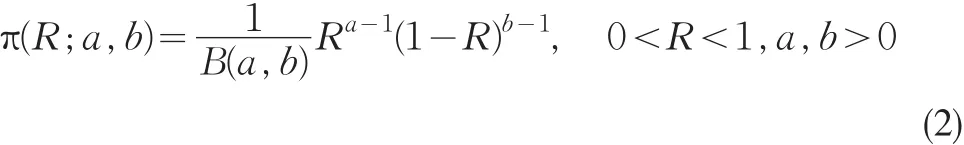
其中a和b为超参数。

在Bayes统计推断的讨论中,损失函数是必不可少的,最常用的损失函数为平方误差损失函数,该损失函数赋予了高估和低估于同样的损失,然而在估计可靠性和失效率函数时高估往往会带来更加严重的后果,这时对称损失函数就显现出不足之处,且我们最常使用平方误差损失函数的另一个原因也仅是因为其在数学上通常更加容易处理。然而随着计算技术的飞速发展,一些繁杂的积分运算已不是难事。于是近年来很多学者提出了一些比较有用的非对称损失函数,如LINEX损失函数、熵损失函数就是其中最常用的两种，本文将在如下一类非对称损失函数[8]下

讨论几何分布可靠度的Bayes估计问题。

并且解是唯一的。

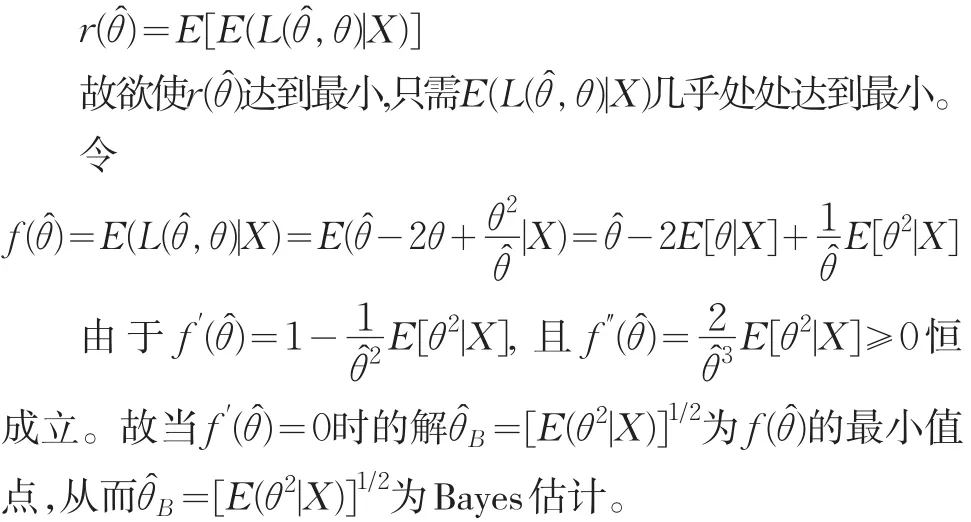
下证唯一性：由于损失函数(3)为严凸损失函数,故该Bayes估计是唯一的。

2 可靠度的估计

在这一部分我们将在非对称损失函数

下,讨论可靠度R的估计问题.

2.1 可靠度的Bayes估计

定理2.1在几何分布（1）中,若R的先验分布为Beta分布Be(a,b),在非对称损失函数(5)下,可靠度R的唯一的Bayes估计为：

证明 在几何分布（1）中,若R的先验分布为Beta分布Be(a,b),得可靠度R的后验概率密度函数为

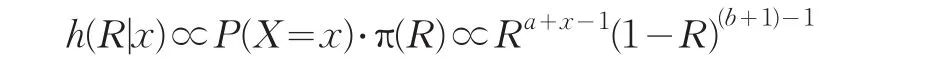
则该后验概率分布为贝塔分布Beta(a+x,b+1)从而在非对称损失函数(5)下,由引理1.1得可靠度R的唯一的Bayes估计为：

2.2 可靠度的多层Bayes估计

在高可靠数据情况下,几何分布可靠度R大的可能性大,小的可能性小,于是韩明提出了选取R的先验分布的构造方法-增函数法[9]。即选取R的增函数作为R的先验概率密度的核,它符合R大的可能性大,而R小的可能性小的要求。于是选择较为合理的先验分布成了我们关注的重点。在几何分布(1)中,若设R的先验分布为Beta分布Be(a,b),其中 a＞0, b＞0为超参数,并假设a与b相互独立,如何确定a与b这两个超参数呢？由于a与b取不同的值时,Beta分布曲线的差异较大,在a≠1或b≠1的情况下,Beta分布可分为以下四种情况(i) a＞1与b＞1,(ii) a＜1与b＜1,(iii) a＞1与b＜1,(iv) a＜1与b＞1,在这四类中只有第(3)类Beta分布的概率密度函数R的增函数,它符合R大的可能性大,R小的可能性小。这样可以确定超参数a与b的范围：a＞1,0＜b＜1,在Bayes估计(6)中,我们需要知道超参数a与b的值才能使用,但是如果我们不能根据自己的经验较为准确的地给出a与b的值,那么得到的Bayes估计的稳定性较差,为改善这种情况,Lindley和Smith在文[6]中提出了多层先验分布的想法,即在先验分布中含有超参数时,可对超参数再给一个先验分布。于是根据上面的讨论我们选取超参数a与b的先验分布。分别为：π2(a)=U(1,C),π3(b)=U(0,1),C为常数.考虑到Beta分布的性质,在0＜b＜1的情况下,a越大,Beta分布的密度函数的尾部越细,从多层Bayes估计的稳健性[11]的角度来看,尾部越细的先验分布常使Bayes估计的稳健性差,因此,a不宜过大,应有一个界限.在计算中C在2至8中取值是适宜的（如可居中取C=5）。由此可得：

定理2.2设几何分布(1)的可靠度R的先验分布为Beta分布Beta(a,b),其中a＞1,0＜b＜1,并且a与b的先验分布分别为：π3(a)=U(1,C),π4(b)=U(0,1),C＞1为常数,则R的多层Bayes估计为：

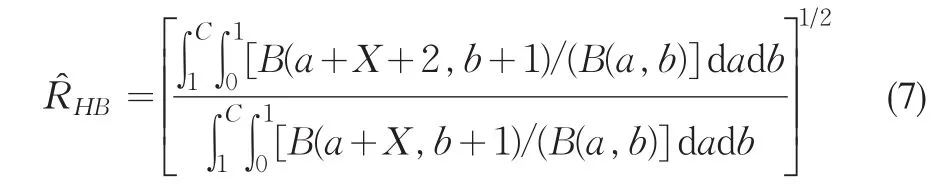
证明 在几何分布(1)中,若R的先验分布为Beta分布,密度函数为：

π1(R/a,b)=Ra-1(1-R)b-1/B(a,b), a＞1, 0＜b＜1为超参数,0＜R＜1,

其中π2(a)=U(1,C),π3(b)=U(0,1),C＞1为常数,则R的先验分布为：

3 数值比较和结论

对某产品进行实验,若在20次贝努里试验中前19次成功而第20次不成功（失败）,在非对称损失函数(5)下,计算几何分布可靠度的多层Bayes估计值。并将其与文[1]中得到的可靠度的多层Bayes估计RˆHB1进行比较。见表1(其中2≤C≤6)。

表1 可靠度的估计结果

从表1知,当2≤C≤6时,非对称损失函数（5）下得到的可靠度的估计的极差更小,从而估计结果更加稳健。并且19次成功,第20次不成功的频率估计值为19/20=0.95,这与本文的结果也更接近,故建议采用本文提出的多层Bayes估计对高可靠性数据情形下几何分布可靠度的计算方法。

[1]韩明,崔玉萍.几何分布可靠度估计[J].运筹与管理,2001,10(4).

[2]赵喜林.几何分布可靠度的截尾Bayes估计[J].武汉科技大学学报,2004,3(1).

[3]徐晓岭,孙祝岭,王磊.几何分布参数的区间估计和统计贴近度研究[J].强度与环境,2005,32(2).

[4]徐晓岭,王蓉华,费鹤良.几何分布产品定数截尾场合下参数的点估计[J].强度与环境,2009,36(2).

[5]韩明.多层先验分布的构造及其应用[J].运筹与管理,1997,6(3).

[6]Lindley,D.V.,Smith,A.F.Bayes Estimation for the Linear Model[J].Journal of the Royal Statistical Society，Series B.,1972,(34).

[7]Berger,J.O.Statistical Decision Theory and Bayesian Analysis,(2ndEdition.)[M].New York:Spring-Verg,1985.

O212.1

A

1002-6487（2013）04-0069-02

张国林（1969-），男，江西丰城人,讲师,研究方向:数据处理和统计决策。

（责任编辑/浩 天）