速率理论中涡流扩散项的置换模拟与经济学思考

游士兵，吴 比，张 佩，毛锴苑，夏素云

（武汉大学经济与管理学院，武汉 430072）

速率理论中涡流扩散项的置换模拟与经济学思考

游士兵，吴 比，张 佩，毛锴苑，夏素云

（武汉大学经济与管理学院，武汉 430072）

基于色谱分析的速率理论，文章对涡流扩散过程进行模拟和置换。涡流扩散是速率理论中引起色谱峰扩张的一个基本因素，即同一组分分子沿色谱柱内各路径形成紊乱的涡流流动。以消费者行为为研究对象，认为涡流扩散体现在消费者由于消费场所区域分布或外界环境的刺激而发生消费滞后或消费提前的行为。模拟结果表明，经济领域的涡流扩散项的存在会使色谱峰展宽，从而分离效果下降。

色谱经济分析法；涡流扩散；滞后消费；提前消费

0 引言

游士兵等（2011）在前期的有关色谱经济分析法的研究中对色谱经济分析法中的有关概念（分配比、保留时间等）做出了相应的置换，并对塔板理论进行了模拟，初步阐明了待分离物质通过色谱柱形成流出曲线的内在机制（游士兵等，2012）。塔板理论所依据的平衡分配在色谱过程中只是一种理想和极限状态，它忽略了色谱过程中分子扩散、传质阻力等因素，故其理论假设未能全面反映色谱分离本质。而速率理论正是在此基础上，把色谱过程看作一个动态非平衡过程，研究过程中的动力学因素对峰展宽（即柱效）的影响，在一定的程度上弥补塔板理论的不足。游士兵等（2013）对分子扩散项进行了经济学思考和置换，并模拟了分子扩散项对消费者不同组分分离的影响。基于此，本文将对速率理论进行进一步探究与现实模拟。

1 速率理论置换理论

在速率理论之分子扩散项的置换研究中，游士兵等（2013）对速率理论的基本原理进行了详细阐述，以1956年荷兰学者Van Deemter等提出的色谱过程的动力学理论-速率理论为代表。速率理论，是在吸收塔板理论中塔板高度（H）这一概念的前提下，充分考虑组分在两相间的扩散与传质过程，从而在动力学基础上较好解释影响板高H各种因素的理论。其理论模型Van Deemter方程的数学简化式为：

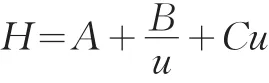
其中 A=2λdp为流动相平均线速度，A=2λdp、A=2λdp、A=2λdp为常数分别代表涡流扩散项系数、分子扩散项系数、传质阻力项系数。当色谱柱内同时起步的组分随流动相在固定相颗粒间的空隙间穿行，朝柱出口方向移动，如果固定相颗粒不均匀，则组分在穿过这些空隙时碰到大小不一的颗粒而必须不断地改变方向，由于路径的不同，会在柱内形成了紊乱的“涡流”的流动，使流经障碍情况不同的流路中的分子先后到达柱出口，而使谱带展宽。

鉴于分子扩散项已在之前的研究中予以讨论，本文以涡流扩散项A作为置换对象进行讨论，传质阻力项将另文研究。

2 涡流扩散项（A）及其置换思考

2.1 涡流扩散项（A）

在填充色谱柱中，当组分随流动相向柱出口迁移时，流动相由于受到固定相颗粒障碍，不断改变流动方向，使组分分子在前进中形成紊乱的类似“涡流”的流动，故称涡流扩散。流动相沿柱内各路径形成紊乱的涡流运动，有些组分分子沿较窄或较直的路径运行，以比较快的速度通过色谱柱，发生分子超前；而另一些组分分子沿较宽或弯曲的路径运动，迁移速度比较慢，发生分子滞后；介于二者平均路径的分子，则处于中间。假若以组分分子中间路径为准，那么某些分子显然或前或后到达柱出口处，使冲洗它们的时间产生一个统计分布，即色谱峰具有一定展宽。

组分不同路径的流速差异会引起组分流出曲线的扩张，用公式表现为：

式中，λ为常数项，称为填充不规则因子，dp为固定相的直径。λ取决于固定相大小、分布范围及填充方法。λ越大表明色谱柱填充越不均匀，当固定相间孔隙越不一致，分子走过的路径差别越大，则距离偏差越大，峰形越加宽。对于dp小的颗粒，组分分子移动步幅小，不仅可以补偿由于固定相颗粒小而使不均匀因子λ值的增加，而且可以使整个A=2λdp值下降。所以，在色谱柱系统可能的情况下，尽量选择细颗粒固定相填充均匀。

2.2 涡流扩散项的置换思考

2.2.1 涡流扩散项

本文为旨在探究涡流扩散项在色谱经济学领域的定义及置换问题。在塔板理论中，色谱柱被认为是均匀填充的，而速率理论假设色谱柱是非均匀填充的，这种假设更加符合现实状况。在化学领域中，填充不均匀会导致进入色谱柱同一组分物质路径的不同。故涡流扩散从本质上来说，是由于待分离物质受到固定相的阻碍作用。这种阻碍作用不同于固定相对组分的化学作用（如溶解或吸附），而是固定相对组分在路径上的阻碍作用，因此它并不会改变组分的分配比，而是使组分分子在前进中形成紊乱的类似“涡流”的流动。

经济学研究的是经济主体的决策问题，所以化学领域中的组分在经济领域中被置换为像个人、家庭、企业这样的行为主体，而流动相和固定相被置换为某种倾向（如消费倾向、分红倾向、投资倾向等）。换言之，在经济领域中，固定相是阻碍行为主体进行某种行为的一种倾向，这种带有阻碍性质的倾向除了决定主体的行为结果，还会使主体在行动过程中形成类似“涡流”的运动。经济领域的涡流扩散运动，在形式上虽然表现为一种“随机游走”状态，但是在时间和空间上又会与一些经济因素存在一定联系，在经济学中，我们通常用解释变量和被解释变量来表示相关经济现象的内在联系。

以消费行为为例，消费者会出现两种情况的涡流运动，一种是消费者已形成的消费决策不得不滞后完成，即以较弯或长的路径运行，延迟进入到下一塔板；一种是消费者已形成的消费决策会提前完成，即以较直或短的路径运行，更快地进入到下一塔板。换言之，消费者在消费倾向的作用下形成了消费决策，不一定会立刻得到实行。当这种消费行为由于外界经济环境的影响不得不滞后或提前时，经济领域的涡流扩散就形成了。在本文中，我们假设消费者之所以会滞后消费，可能是源于消费者与消费目的地之间的距离，此时消费者需要耗费更多的时间在准备和前往目的地；而消费者之所以会提前消费，可能是在优惠券到期的驱动或者“从众”心理，或者政策环境或者促销活动等提前了原来的消费打算。

2.2.2 涡流扩散项的影响因素及其置换

在化学领域中，涡流扩散会引起组分流出曲线的扩张，用公式表现为：A=2λdp。涡流扩散项取决于填充不规则因子λ和固定相的直径dp有关。

（1）填充不规则因子λ

当固定相间孔隙越不一致，分子走过的路径差别越大，即λ越大表明色谱柱填充越不均匀。以消费行为为例，固定相是阻碍消费者进行消费的倾向。即使消费者已经形成消费倾向，也可能由于固定相的个体差异导致消费行为实现的不同。在分配比保持不变时，若消费者的消费行为发生滞后或提前，消费者会由于涡流运动而引起组分流出曲线的扩张。所以，λ在经济领域中衡量的仍是色谱柱的填充不规则程度。

填充不规则因子λ被置换为全部消费者与目标消费场所距离的标准差，衡量的是消费场所分布的便利性，在一定程度上体现了消费场所区域分布的合理性。当消费者距离目标消费场所较远时，消费者不得不在准备和路程上花费更多时间，从而导致消费行为的相对滞后；当消费者距离目标消费场所很近时，消费者可能会立刻将消费决策付诸实践，从而造成消费行为的相对提前。所以，消费者与目标消费场所距离的标准差λ通过影响消费行为的实施速度，形成经济领域的“涡流”。

（2）固定相直径dp

化学领域中，dp是影响涡流扩散项A=2λdp的重要因素。一方面，在其他条件相同时，dp越大涡流扩散效果越显著；另一方面，dp会通过影响λ从而改变A=2λdp值。经济领域中，由于λ为全部消费者与目标消费场所距离的标准差，是一个常数项，并不直接取决于dp，但λ和dp之间仍然存在相关关系。当消费场所区域分布越合理，即λ越小时，消费者对外界环境的敏感程度也会越强。

固定相直径dp被置换为消费者对外界环境的敏感性。这里的外界环境主要是指可能会影响消费行为的实现的经济环境因素，包括优惠券的到期、商品促销活动、新开张的商业街、以及银行利率的变化等。当消费者对上述经济环境因素足够敏感时，可能会引起消费行为的提前或滞后；当消费者对上述经济环境极不敏感时，可能根本不会改变已有的消费决策，所以消费者对外界环境的敏感性dp通过影响消费行为的实施速度，形成经济领域的“涡流”。

3 对消费者行为的速率理论置换实例及模拟

3.1 分离过程假设

本文沿用游士兵等（2012）塔板理论中的研究，以特定消费群体的消费行为为研究对象，对速率理论中的涡流扩散项进行置换。有如下假设：

⑴假设待分类组分为两类消费群体，这些消费人群对于可支配收入只有两种选择——消费和储蓄。其中，流动相为消费倾向，固定相为储蓄倾向，且A类消费群体的分配比k=1：1，B类消费群体的分配比为1：4。

⑵假设可支配收入以脉冲式增加，且每次增加M元。当可支配收入每增加一次时，消费者会进行一次消费和储蓄的选择。

⑶若考虑涡流扩散，则消费者会出现两种情况的涡流运动，一种是消费者已形成的消费决策不得不滞后完成，即以较弯或长的路径运行，延迟进入到下一塔板；一种是消费者已形成的消费决策会提前完成，即以较直或短的路径运行，提前进入到下一塔板。

⑷为了更简单明了地体现涡流扩散作用，本文假设消费行为滞后的时间间隔为T=1，即消费者在t期形成的消费决策并没有在t期实现，而是在t+1期才进行消费。在色谱柱中，表现为原本在t期应该进入下一塔板的消费者在t+1期才完成该行为。同样，消费行为提前的时间间隔也设为T=1。

3.2 速率理论模拟

以下模拟过程以上述分离过程假设为基础，当可支配收入约束每增加一次时，消费者在消费和储蓄之间进行一次选择。于是，前一个塔板中的消费者有一半选择进入下一个塔板（即选择消费），同时另一半消费者由于选择储蓄会留在原塔板中。在不存在涡流扩散的情况下，经过多次的分配平衡后，A类消费群体会形成如表1中的分配情况。可以看到，t=2时，塔板1上的50位消费者中有25位消费者进入塔板2，如表1所示。

表1 不存在涡流扩散的分配情况（分配比k=1）

3.2.1 待分离组分为单一组分的流出曲线

（1）消费者存在消费行为的滞后

考虑涡流扩散作用，以第一种情况为例，假设t=3时，塔板1中的25位消费者里有10位消费者可能由于消费场所区域分布问题，不得不延迟消费。由于消费行为滞后的时间间隔设为T=1，则可支配收入约束再次增加时，这10位消费者会继续之前的消费。于是，这10位消费者在t=4才进入下一个塔板（塔板2），表现为t=3时塔板中的消费者仅有15位进入到下一塔板，而有35位留在原塔板。表2反映了消费者选择提前消费时塔板内的组分分布情况，是涡流扩散作用的核心体现。

表2 消费者存在提前消费行为下3、4塔板的分配情况①对于存在涡流扩散项的情况，为简单起见表2，表4只显示第2、3、4次脉冲情况下的塔板分配情况，整个分配过程则分别在表3、表5中予以描述。

存在第一类涡流扩散的A类消费群体的分配表如表3所示。

表3 存在第一类涡流扩散的分配情况（分配比k=1）

3.2.2 消费者存在消费行为的提前

考虑涡流扩散，以第二种情况为例，消费者可能由于外界经济环境的刺激（比如消费券的到期、商品促销活动等），在效用最大化原则下会选择提前已有的消费打算。不妨假设t=4时塔板1中的50位消费者，有10位在经济环境刺激下影响选择提前消费。于是，这10位消费者在t=3时即进入下一个塔板（塔板2），表现为t=2时塔板中的消费者有35位进入到下一塔板，而有15位留在原塔板。表4反映了消费者选择提前消费时塔板内的组分分布情况，是涡流扩散作用的核心体现。

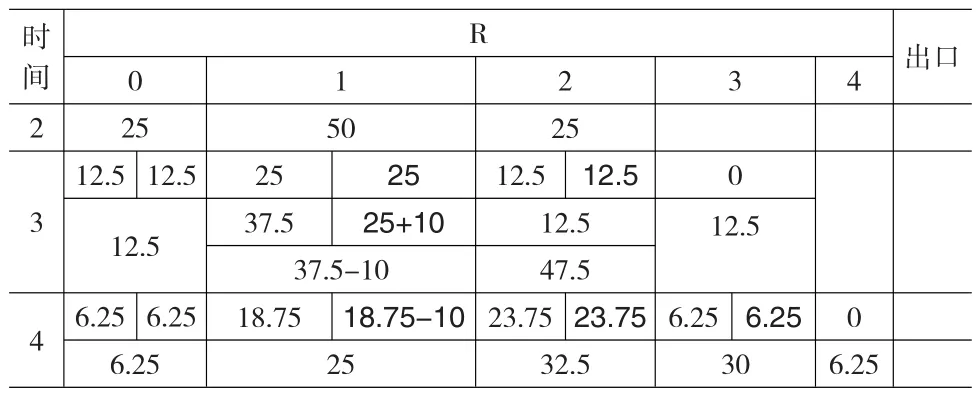
表4 消费者存在提前消费行为下3、4塔板的分配情况

如表5所示，其为存在第二类涡流扩散情况的的完整分配表。

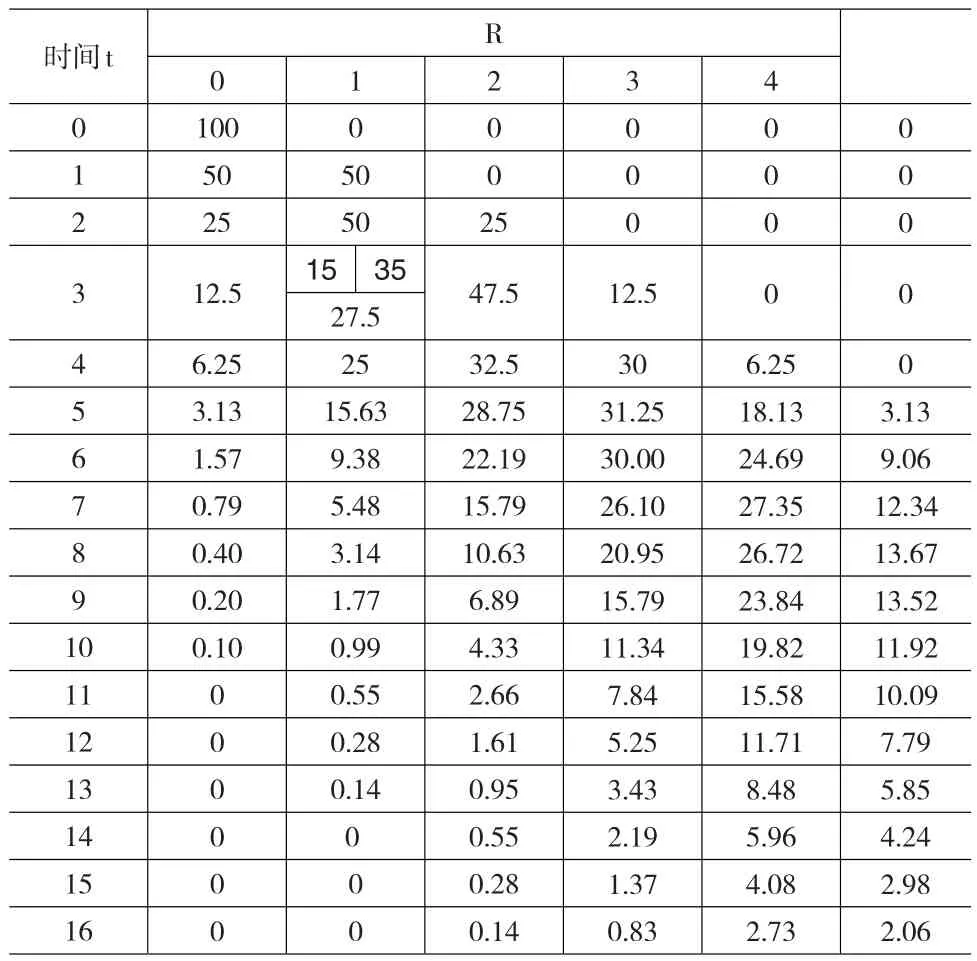
表5 存在第二类涡流扩散的分配情况（分配比k=1）

图1 三种消费行为流出曲线的比较

从三种消费行为的流出曲线可以看出，相对于不存在涡流扩散相的情况，滞后消费行为主要表现为峰的向右扩张；提前消费行为则主要为峰的向左扩张。结果与实际经济生活相吻合，可以认为滞后消费行为的存在使得更多消费者在后阶段时期进行消费，反之。现实中，涡流扩散的存在会同时使消费行为提前或滞后的情形，所以更普遍的情况应是流出曲线双向展宽。

3.2.2 待分离组分为混合物的流出曲线

现考虑B类消费群体（分配比为1：4），在此仅考虑存在滞后消费的涡流扩散作用。假设t=3时，塔板1中的32位消费者里有10位消费者可能由于消费场所区域分布问题，不得不延迟消费。由于消费行为滞后的时间间隔设为T=1，于是，这10位消费者在t=4才进入下一个塔板（塔板2），表现为t=3时塔板中的消费者仅有15.6位进入到下一塔板，而有19.6位留在原塔板。表5给出了B类消费者选择提前消费时塔板内的组分分布情况。

表5 情况下消费者存在滞后消费行为3、4塔板的分配情况(k=1：4)

在表6中给出了B类消费者中存在滞后消费情况下的塔板分配情况。

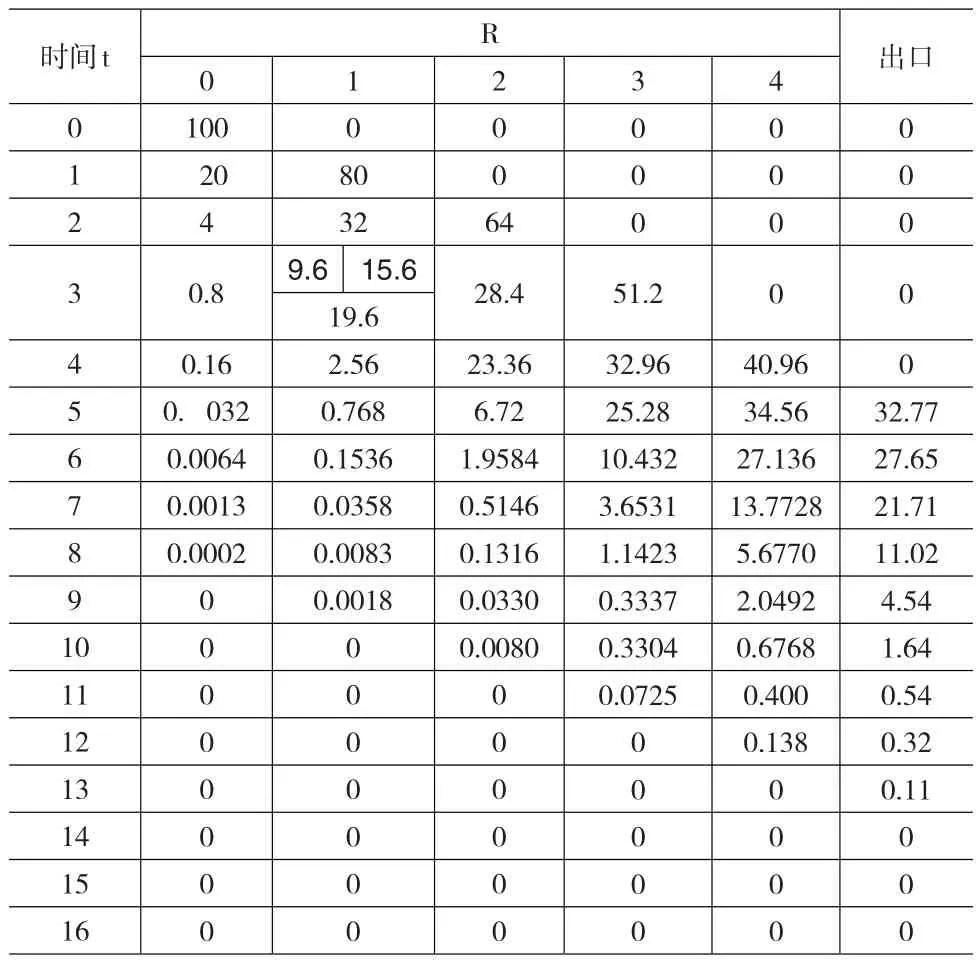
表6 存在第二类涡流扩散相的消费情况（k=1：4）

根据以上分配结果，可得到A、B两类消费群体的流出曲线。其中，图2为不存在涡流扩散下的流出曲线；图3为存在涡流扩散下的流出曲线图。

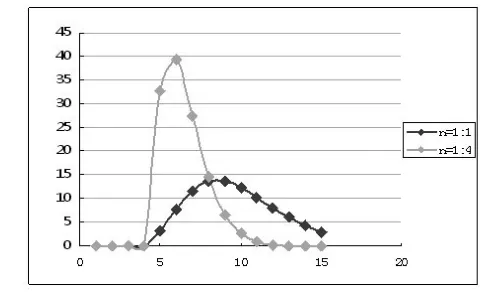
图2 不存在涡流扩散的流出曲线

图3 存在涡流扩散的流出曲线

3.3 结果与分析

速率理论假设色谱柱为非均匀填充，而不均匀的填充会导致涡流扩散作用的存在，从而使得峰宽扩展。填充不均匀导致进入色谱柱同一组分物质路径的不同，组分分子的路径可大致分为三种情况：第一，填充均匀状态下的路径；第二，填充密度相对较大时的路径；第三，填充密度相对较小时的路径。上述过程即置换和模拟了经济领域中的这一情况，第一种情况（表1）即为塔板理论下的状况，后面两种情况（表3、表5）分别对应着上例中消费行为的滞后和提前。在一类消费群体中，消费行为的提前和滞后往往共存。为了方便起见，表3、表5对这两种消费情况分别进行模拟。从图1中可以看出，当消费者选择滞后消费时，流出曲线相对向右展宽；当消费者选择提前消费时，流出曲线相对向左展宽。现实中，涡流扩散的存在会同时使消费行为提前或滞后的情形，所以更普遍的情况应是流出曲线双向展宽。

由于待分离物质为两类消费群体，在不存在涡流扩散时流出曲线如图2所示，当存在涡流扩散时，A、B类消费者峰同时展宽，分离效果有所变差，增加了混合组分分离的难度。在现实经济生活中，因经济环境或个体差异等原因导致的滞后消费和提前消费普遍存在，任何影响填充不规则因子λ和固定相的直径dp的因素都会引起涡流扩散项的改变，从而使得某些消费者的消费行为发生滞后或提前，那么某些分子显然或前或后到达柱出口处，使冲洗它们的时间产生一个统计分布，即色谱峰具有一定展宽。当待分离物质为混合组分时，由于各组分的分配系数有差异，不同组分的色谱峰会相应展宽，流出曲线会有较大的重合，从而使得分离效果降低，整个色谱柱的柱效下降。在经济领域中，涡流扩散作用是普遍存在的经济现象，本文着重讨论填充不均匀时复杂经济中的组分分离效果不能达到理想状态、分离效率降低的情况，使得色谱经济分析法的运用更加贴近经济现实。理论上，本文旨在对存在涡流扩散相情况下组分的流出情况做详尽描述，弥补塔板理论的不足也为后续研究打下坚实基础。实际运用中，本文为把握消费者行为、制定相关政策建议提供新的切入点。

4 结语

本文以消费者的消费行为为研究对象，对速率理论中的涡流扩散现象进行初步探究与现实模拟。涡流扩散是速率理论中引起色谱峰扩张的一个基本因素，即组分分子沿色谱柱内各路径形成紊乱的涡流流动。以消费行为为例，λ被置换为消费者与目标消费场所距离的标准差，dp被置换为消费者对外界环境的敏感性，由于消费者已形成的消费决策可能由于消费场所区域分布（λ）和外界环境的刺激（dp）而发生消费滞后或提前，这种改变“路径”的消费行为于是形成了类似化学领域的涡流运动。模拟的结果表明，当消费者选择滞后消费时，流出曲线相对向右展宽；当消费者选择提前消费时，流出曲线相对向左展宽。现实中，由于消费行为的提前和滞后同时发生，故经济领域的涡流扩散最终会造成峰的展宽。本文的研究重点在于涡流扩散，后续的研究会关注速率理论的传质阻力，以期对速率理论进行深入全面的研究。

[1]游士兵,吴比,沈萍,梅敏,苏正华.复杂经济现象分类方法创新的理论前瞻——基于化学“色谱分析法”的借鉴与思考[J].统计与决策，2011，（7）.

[2]游士兵，梅敏，吴比.色谱分析法在经济领域中的应用展望[J].统计与决策,2011（,11）.

[3]沈萍，张佩，毛锴苑，李跟强，游士兵.色谱经济分析法置换系列研究：分配比[J].统计与决策，2011，（7）.

[4]沈萍，游士兵，毛锴苑，张佩，李跟强.色谱经济分析法置换系列研究：保留时间[J].统计与决策，2012，（13）.

[5]苏立强，郑永杰.色谱分析法[M].第1版.北京:清华大学出版社.2009.

[6]游士兵，苏正华，崔娅雯，杨艺芳，陈蔚妮.速率理论中分子扩散项的置换模拟与经济学[J].统计与决策，2013，（1）.

F069

A

1002-6487（2013）04-0004-04

教育部博士研究生学术新人奖资助项目（5052011105002）；中央高校基本科研业务费专项资金资助项目（201110501020001）

游士兵（1964-），男，湖北天门人，教授，博士生导师，研究方向：统计学、数量经济学。

吴 比（1987-），男，黑龙江大庆人，博士研究生，研究方向：统计学。

（责任编辑/亦 民）