无量纲化对属性权重影响的传导机制及调权研究

糜万俊

(南京理工大学自动化学院，南京 210094)

无量纲化对属性权重影响的传导机制及调权研究

糜万俊

(南京理工大学自动化学院，南京 210094)

文章基于离差最大化要求的约束条件与假设冲突以及离差最大化可能造成权重信息失真的问题，以属性下方案的方差为媒介，分析了无量纲化方法对属性权重影响的传导机制，给出了几个重要的结论。同时，依据方差控制要求，给出了权重调整策略，最后通过算例分析对结论进行了检验。

综合评价；无量纲化；方差控制；调权

0 引言

属性值和属性权重是多属性决策的两个重要因素。权重确定有主观赋权法（AHP法等）、客观赋权法（熵法等）和组合赋权法[1-7]等。由于属性之间的矛盾性和不可公度性，需要进行无量纲化处理。

在权重方面，文[8]以决策信息离差最大设计权重模型，文[10-13]提出离差最大化方法求解权重并应用，其中文[9]定义约束条件为属性权重平方和为1，文[10]认为只要目标函数中权重系数小于约束条件的权重系数均可以获得最优解。文[14]在分析无量纲化对权重影响时，也使用了这个约束条件，但这与假设矛盾。

在无量纲化处理方面，从解的唯一性和有效性、被评价对象间的局部差异和整体差异等角度出发，文[14-15]分析了标准化处理法、极值处理法、线性比例法、向量规范化和功效系数法等无量纲化方法对方差的影响。

在多属性决策中，属性值的无量纲化对决策方案的方差有着一定的影响，而这种影响间接对权重造成影响，分析这种影响关系对于实现有效决策尤为重要。本文将重点研究无量纲化对属性方差的影响，以及属性方差对属性权重的影响，并揭示影响机制。

1 多属性决策下无量纲化

设A={ai|i=1,2,…,n}为某多属性决策问题的方案集，设定方案的属性相同，为：G={Gj|j=1,2,…,m}。在Gj下，ai的属性值为xij(i=1,2,…,n;j=1,2,…,m)，决策矩阵A和无量纲化后矩阵Z记为：A=(xij)n×m,Z=(zij)n×m。常用无量纲化方法主要有：

（1）极差变换法：如果Mj,mj分别是Gj下所有属性值的最大值和最小值，如果Gj为效益型，则：zij=(xij-mj)/(Mj-mj)；如果Gj为成本型，则：zij=(Mj-xij)/(Mj-mj)。

（4）标准化处理法：这种变换对xij没有特殊要求。设sj分别是属性Gj的样本均值和样本均方差，则：

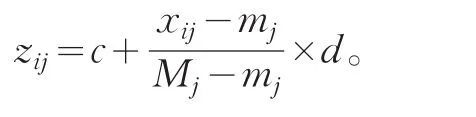
2 无量纲化下的样本方差和权重

不同的无量纲化方法可以产生不同的方差，而不同的方差也会得到不同的权重。

上述6种无量纲化方法中，s(Xj)均为无量纲化处理前属性值的方差值，即对不同的无量纲化方法而言，同一Gj下s(Xj)均相同。

3 无量纲化对综合评价的影响

（1）功效系数法和极差变换法得到的结果不同，但传导到权重方面却是相同的权重。无量纲化传导的方案排序结果和方案评估值的方差是与d相关，与c无关。

（3）线性比例法、向量规范法和归一化方法对原有数据的压缩程度呈现递减趋势，但传导给权重的趋势却不明显，进而对排序和方案的影响也不明显。

4 基于方差的无量纲化方法选择

(1)由于功效系数法和极差变换法得到的排序结果仅仅与d有关，因此取d＞0比较合适。当d=1时两者排序结果正好相同。如果此时的方差达不到要求，可以适当增加d值，直到其满足多属性决策对方案区分的方差需求。

(2)标准化处理法得到的权重完全相同，退化为风险决策的等权决策问题。

（3）就线性比例法、向量规范法和归一化方法而言，由于权重变化趋势未知，而方差变化已知，如对方案区分度有要求，尽量选择方差较大的无量纲化方法，即线性比例法。

（4）将极差变换法与线性比例法相比，方差还与mj相关。

因此，在考虑方案排序结果方差时，当Mj＞0,mj＞0时，尽量选择极差变换法；当Mj＞0,mj＜0时，尽量选择线性比例法。

5 基于方差的权重调整

以上结果表明：功效系数法和极差变换法选择时，调整方差只需要调整d即可。对线性比例法、向量规范法和归一化方法而言，调整方差主要是调整权重，权重优化主要有两种途径，即实施组合赋权或权重修正。本文就权重修正给出调整策略。

由于基于方差获得的权重是客观权重，故权重的调整幅度越大则信息越失真。在权重调整中，由于总和为1，增加某些属性的权重值就需要减少某些属性权重值。于是，设置如下调整原则：

原则1：优先调整方差最大的属性权重和方差最小的属性权重。

理由：增加方差最大的属性权重则可实现s2较快增长，而同时减少方差最小的属性权重，则减小的方差最小。

原则2：增加和减少的属性权重值相同。。

理由：如变化的权重不同，则减小的权重值将不会集中于方差最小的属性，那么会减少其他任何属性的权重，则属性方差减少值将会增加，难以较快实现方案区分度的要求。

基于上述调整原则，本文给出无量纲化选择和权重调整步骤：

（1）针对某个多属性决策矩阵，可以采用多种无量纲化方法进行处理。如果选择极差变化法或功效系数法，由于两种方法得到的权重相同，此时不需要调整权重，如果最终的方案评价值方差达不到要求，只需要增加d值，直到满足要求即可。

（2）如果选择线性比例法、向量规范法或归一化方法，建议首选线性比例法。如果其得到的方案评价值方差达不到要求，则将属性的方差按照从大到小的方式进行排序，增加方差最大的属性权重（增加量为γ），减少方差最小的属性权重（减小量为γ）。针对设定的方差要求（不同无量纲化下方差要求是不同的），求解γ的临界点就演化为求解一个二元一次方程。

γ最终要体现到属性权重中，决策者可以设定最大或最小权重的一个范围，如10%。如果在上述合理的范围内变化，最终的方差满足要求，则停止。如果不能满足要求，则找出方差排序第二位和倒数第二位的属性，按照上述要求进行调整即可。

（3）由于线性比例法、向量规范法或归一化方法传导的权重趋势不显著，如果选择了向量规范法或归一化方法，当其最终的方差达不到决策者要求时，可以按照线性比例法调整步骤实现即可。

6 算例

评价进入军品市场的民营企业的综合能力，在突出国防安全和风险管理等因素，并考虑操作性的情况下，一般可以从企业经营信誉G1、质量管理能力G2、企业保密能力G3和企业创新能力G4、企业财务能力G5五个方面进行评估（三级指标就不展开阐述）均为效益型属性。假设对10个民营企业（a1∼a10）进行评价，评价矩阵见表1：

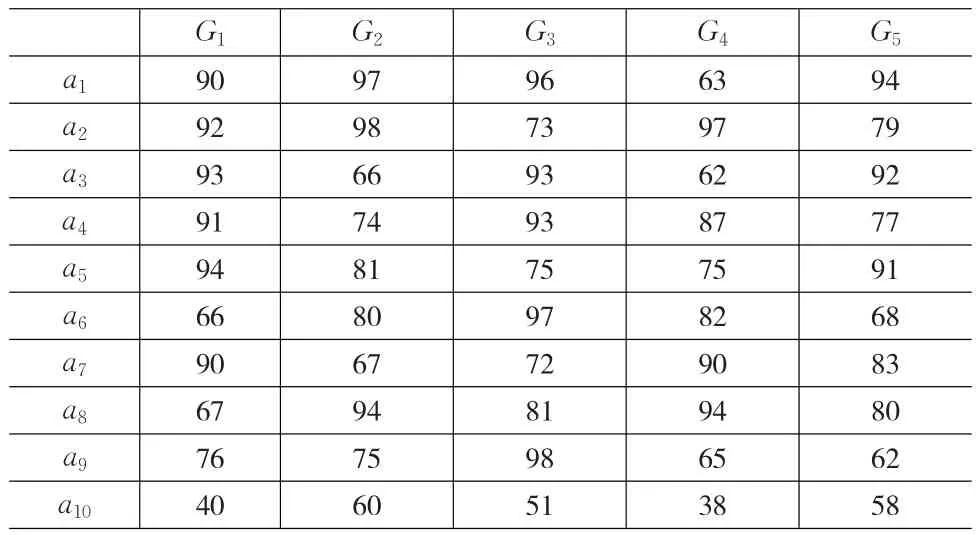
表1 多属性决策矩阵表

按照上述无量纲化方法，得到不同无量纲化下的属性方差，见表2。

表2 无量纲下的属性方差比较表

于是不同无量纲化方法下的属性权重，见表3。

表3 无量纲下的属性权重比较表

（1）在极差变换法下和功效系数法下设定s2=0.05，只有功效系数法（d=2）时方差为0.089922，极差变化法下其方差为0.02248。此时不必改变权重，只要将其按照功效系数法变化，d变化为1.491361即可，c可取任意值。

（2）在线性比例下，设定方差为0.008，变化幅度不超过原有权重的20%。基于方差顺序G4,G1,G3,G2,G5，有γ=0.010041，满足γ设定的阈值要求，调整结束。

在向量规范下，设定方差为0.0009，变化幅度不超过原有权重的20%。有γ=0.021082，满足γ设定的阈值要求，调整结束。

在归一化法，设定方差为0.0001，变化幅度不超过原有权重的20%。此时得到的γ为0.041562，超过了最小权重的20%，于是按照20%进行调整，再次考虑余下的属性，重复上述步骤，得到的调整值为0.018526591，满足要求，调整结束。

7 结论

本文分析了无量纲化对方差以及通过方差对权重的传导机制，避开了传统离差方法要求权重平方和为1以及离差最大化的假设，减少了由于离差最大化可能造成的权重信息失真，为决策者选择合适的无量纲化方法提供理论指导。同时，在某种无量纲化方法下方差达不到要求时，给出有效调整权重策略，并通过算例加以验证。

[1]Ma J,Fan Z P,Huang L H.A Subjective and Objective Integrated Ap⁃proach to Determine Attribute Weights[J].European Journal of Opera⁃tional Research,1999,(112).

[2]Xu XiaoZhan.A Note on the Subjective and Objective Integrated Ap⁃proach to Determine Attribute Weights[J].European Journal of Opera⁃tional Research,2004,156(2).

[3]江文奇.多属性决策的组合赋权优化方法[J].运筹与管理,2006,15(6).

[4]姜昱汐,迟国泰,严丽俊.基于最大熵原理的线性组合赋权方法[J].运筹与管理,2011,(1).

[5]曹清玮,吴坚,梁昌勇.一种基于Yager熵最大化属性权重组合方法[J].运筹与管理,2010,(3).

[6]宋光兴,杨德礼.基于决策者偏好及赋权法一致性的组合赋权法[J].系统工程与电子技术,2004,26(9).

[7]周宇峰,魏法杰.基于相对熵的多属性决策组合赋权方法[J].运筹与管理,2006,15(5).

[8]陈华友.多属性决策中基于离差最大化的组合赋权方法[J].系统工程与电子技术,2004,26(2).

[9]王应明.运用离差最大化方法进行多指标决策与排序[J].系统工程与电子技术,1998,(7).

[10]熊文涛,齐欢,雍龙泉.一种新的基于离差最大化的客观权重确定模型[J].系统工程,2010,28(5).

[11]张国权,李文立,杨件.基于最大离差和最大联合熵的多方案优选方法[J].运筹与管理,2007,16(4).

[12]李刚,迟国泰.级差最大化组合赋权的人的全面发展评价模型及实证[J].中国软科学,2009,(9).

[13]Ying-Ming Wang,Ying Luo.Integration of Correlations with Stan⁃dard Deviations for Determining Attribute Weights in Multiple Attri⁃bute Decision Making[J].Mathematical and Computer Modelling,2010,51.

[14]郭亚军,马凤妹,董庆兴.无量纲化方法对拉开档次法的影响分析[J].管理科学学报,2011,14(5).

[15]郭亚军,综合评价结果的敏感性问题及其实证分析[J].管理科学学报,1998,1(3).

N943

A

1002-6487（2013）04-0011-04

国家自然科学基金资助项目（71071003）；教育部人文社科基金资助项目（09JD630522）

(责任编辑/亦 民)