高阶非线性薛定谔方程的离散梯度法

骆思宇，蒋朝龙，孙建强

(海南大学 信息科学技术学院，海南 海口 570228)

光孤子的概念最早由HASEGAWA 于1973 年提出［1］.HASEGAWA 与TAPPERT［2］合作从理论上证明了任何无损光纤中的光脉冲在传输过程中能形变为孤子后稳定传输.1980 年MOLLEAUER［3］等人提出将光纤中的孤子用做传输信息的载体，构建一种新的光纤通信方案，称为光孤子通信.岳进，方云团等人分别研究了五阶饱和非线性效应下皮秒孤子间相互作用的情况和饱和非线性效应对皮秒孤子传输特性的影响［4-5］.

近年来保结构算法在数值模拟光孤子的传输特性方面具有独特的优势.保结构中辛和多辛算法具有长时间的精确计算能力并能近似地保持系统的能量守恒特性，已广泛应用于KdV 方程、非线性薛定谔方程和Maxwell 方程的计算［6-7］.最近QUISPEL 和MCLACHLAN 等人提出了精确地保持系统守恒特性的离散梯度法，其中包括保Hamilton 系统能量守恒的平均离散梯方法.平均离散梯度方法能精确地保持Hamilton 系统的能量守恒，并且具有很好的精度［8-11］.本文将利用平均离散梯度方法求解高阶非线性薛定谔方程并分析饱和非线性效应和相位对皮秒孤子传输的影响，并与辛算法进行比较分析平均离散梯度法保系统能量守恒的特性.飞秒量级光脉冲的传输特性一直是备受关注的一个领域，光孤子相互作用是其研究的重要内容.

在皮秒光脉冲中，光孤子的传输特性可以由非线性薛定谔方程描述

其中，A 是电场的复振辐包络，x 是脉冲在光纤中传输的距离，τ 为时间坐标，α 是损耗系数，1/β1是群速度，β2对应于二阶色散，γ 是非线性克尔系数.包含五阶饱和非线性效应在内的非线性薛定谔方程为

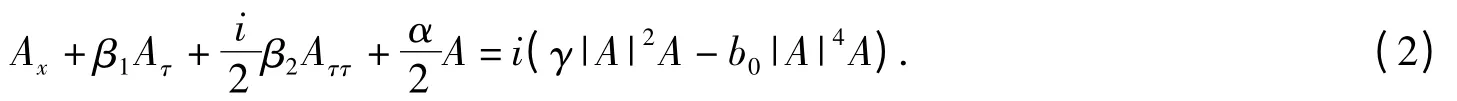
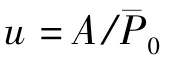
方程(3)具有如下守恒特性

1 离散梯度法

对于给定的Hamilton 系统

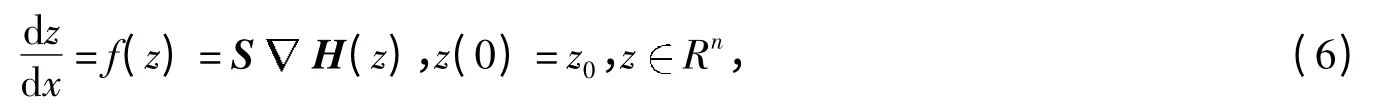
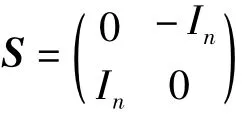
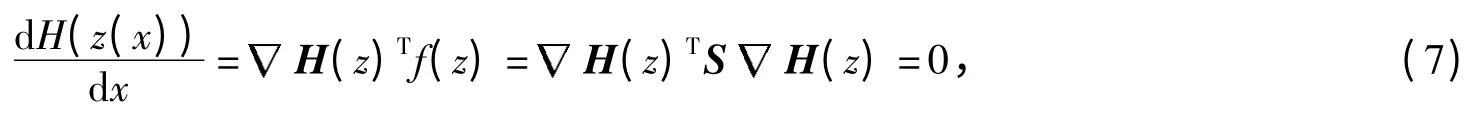
可知Hamilton 系统具有能量守恒特性.

为了让系统在离散后依然保持能量守恒特性，笔者给出二阶精确保Hamilton 系统能量守恒的平均离散梯度法［8］

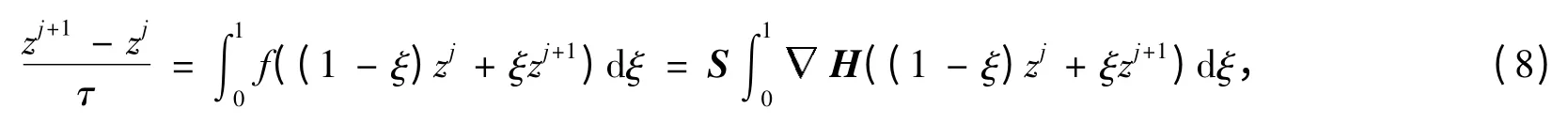
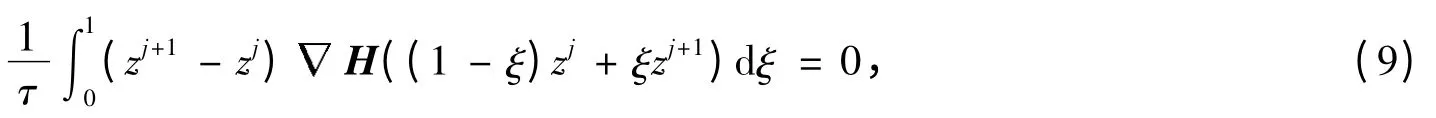
即

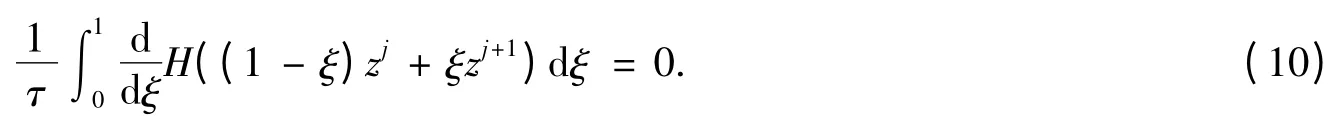
由微积分基本定理，可以得到

方程(11)表明，当式(8)应用于Hamilton 系统(6)时，能精确地保持Hamilton 系统的能量.

2 高阶非线性薛定谔方程的离散梯度格式

令u(s，t)=p(s，t)+q(s，t)i，高阶非线性薛定谔方程(3)等价于

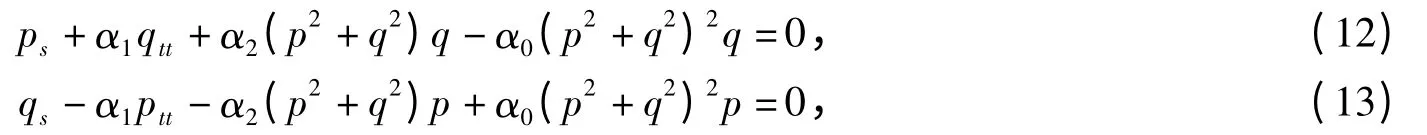
高阶非线性薛定谔方程组(12)和(13)可以写成无限维Hamilton 系统形式

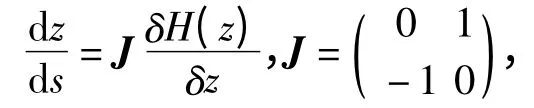
其中，z=(p，q)，Hamilton 函数为

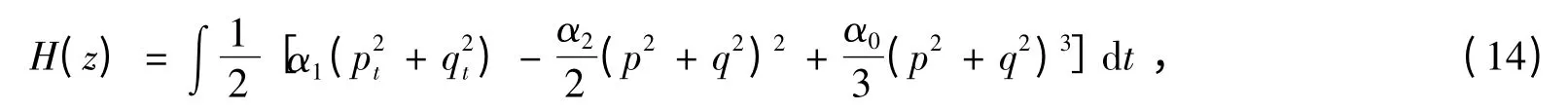
方程(15)的平均离散梯度格式为

将式(17)和(18)化简后，就可以得到高阶非线性薛定谔方程(3)的平均离散梯度格式

为了便于比较，给出非线性薛定谔方程(3)相应的离散辛格式为

3 数值模拟

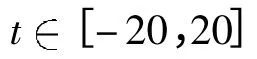
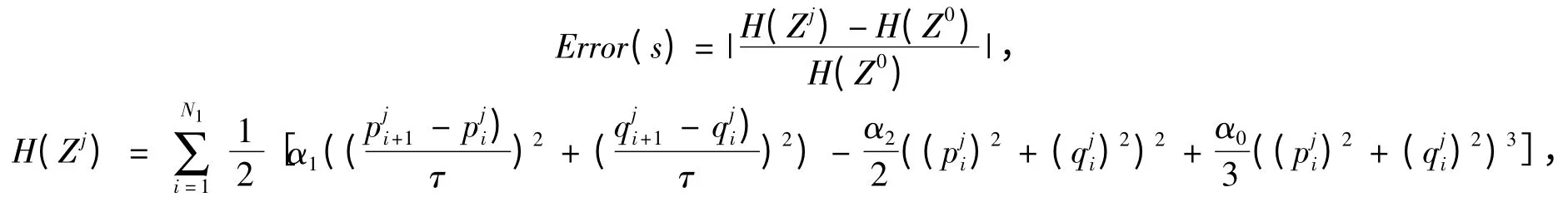
其中，s=jh，Error(s)为s=jh 时的能量相对误差.

首先研究输入皮秒初始脉冲为u(0，t)=r1sech(t-t0/2)+r2sech(t+t0/2)exp(iφ)时［2-4］，不同非线性饱和效应对皮秒孤子演化特性的影响.取h=0.1，τ=0.1.图1 表示相邻等振幅皮秒孤子在间距t0=7，φ=0 时的演化行为，图1(a)是在非线性饱和效应α0=0 时孤子演化行为，图1(b)是在非线性饱和效应α0=0.048 时孤子演化行为.数值结果表明随着非线性饱和效应的增加，非线性饱和效应表现得越明显，孤子碰撞的频率越严重，越不利于孤子脉冲的传输.图2 表示平均离散梯度格式的能量相对误差图，能量相对误差可以到达10-12，能很好地保持方程能量.图3 表示辛格式的能量相对误差图，能量相对误差达到了10-3，只能近似地保持系统的能量.可知非线性饱和效应对孤子有显著的影响，平均梯度法能很好地保持方程的能量，能更加真实地反映皮秒孤子的运动.

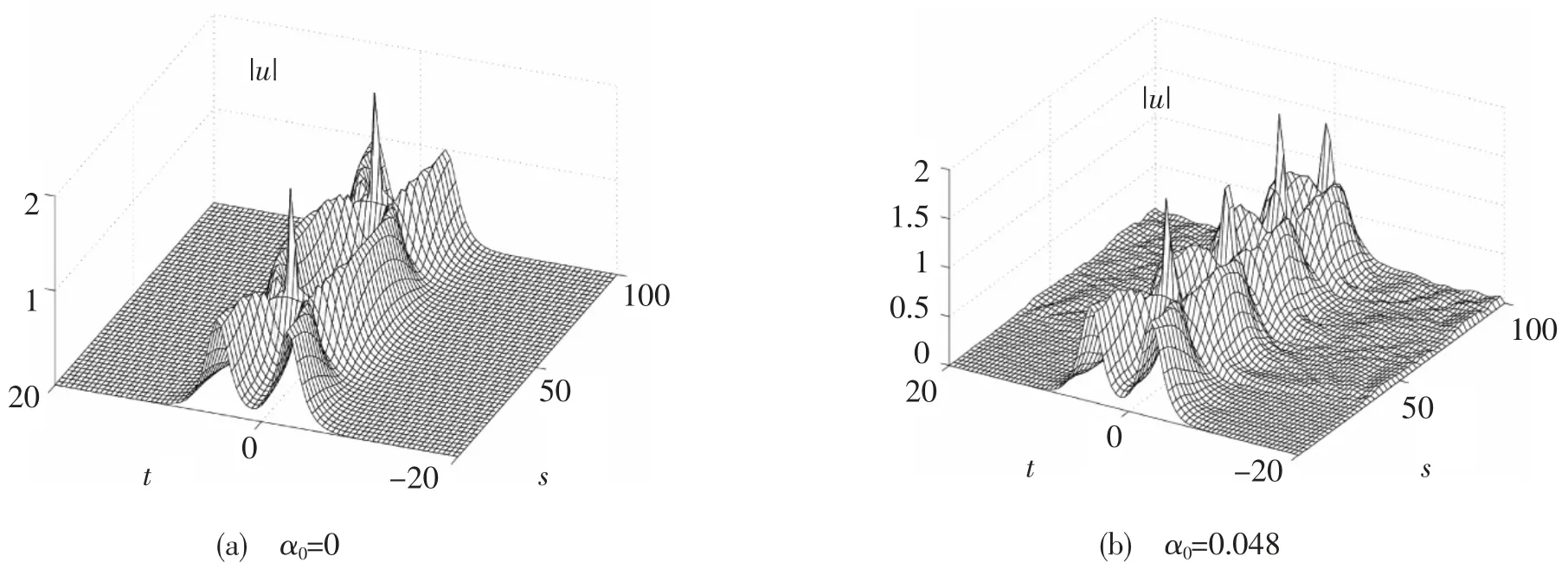
图1 离散梯度格式模拟皮秒孤子演化图

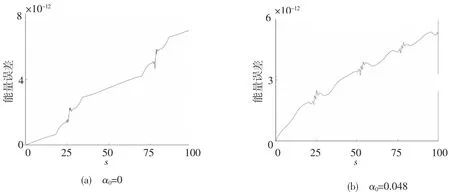
图2 离散梯度格式模拟皮秒孤子的能量误差图

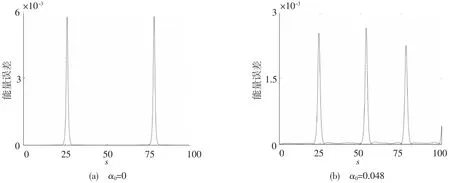
图3 辛格式模拟皮秒孤子的能量误差图

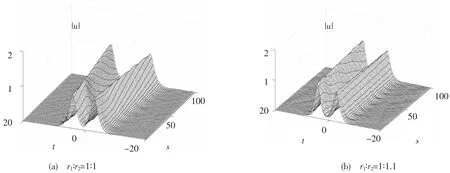
图4 离散梯度格式模拟皮秒孤子演化图

图5 离散梯度格式模拟皮秒孤子的能量误差图

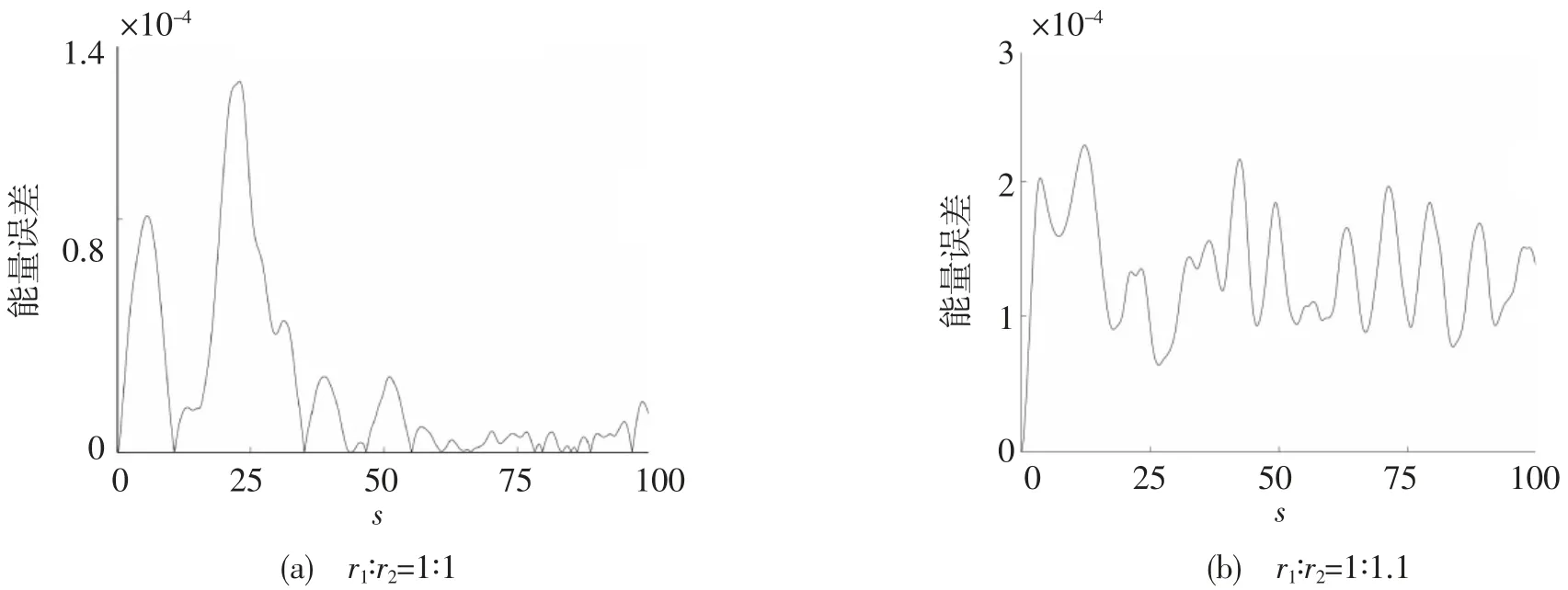
图6 辛格式模拟皮秒孤子的能量误差图

4 小 结

本文构造了高阶非线性薛定谔方程的离散梯度格式，利用高阶非线性薛定谔方程的离散梯度格式，研究了单个和多个光孤子在不同的非线性饱和效应和不同振辐时皮秒光孤子的传输行为，并与高阶非线性薛定谔方程的辛格式进行了比较.数值结果表明，高阶非线性薛定谔方程的离散梯度格式能很好地模拟皮秒光孤子的传输行为，离散梯度法比经典的辛格式能更好地保持系统的能量守恒特性.离散梯度格式在数值模拟具有能量守恒的微分方程中具有独特的优势，能更加真实地反映皮秒孤子运动的客观规律，同样可应用于其他能量守恒的偏微分方程.

［1］HASEGAWA A.Optical Solution in Fiber［M］.Berlin:Spring-Verlag，1989.

［2］HASEGAWA A，TAPPERT F.Transmission of stationary nonlinear optical pulses in dispersive dielectric fibers.Ⅰ.Anomalous dispersion［J］.Appl.Phys.Lett.，1973，23(4):142-144.

［3］MOLLENAUER L F，STOLEN R H，GORDON J P.Experimental observation of picosecond pulse narrowing and solitons in optical fibers［J］.Phys.Rev.Lett.，1980，45(13):1095-1098.

［4］岳进.饱和非线性光纤中孤子传输特性的数值研究［J］.太原师范大学学报:自然科学版，2008，7(1):103-107.

［5］方云团，王永顺，沈廷根，等.孤子对在饱和介质中的传输［J］.量子电子学报，2003，20(6):738-740.

［6］FENG K，QIN M Z.Symplectic Geometric Algorithms for Hamiltonian Systems［M］.Zhejiang:Zhejiang Publishing United Group Zhejiang Science and Technology Publishing House，Heidelberg:Spring-Verlag，2010.

［7］秦孟兆，王雨顺.偏微分方程中的保结构算法［M］.浙江:浙江科学技术出版社，2011.

［8］QUISPEL G R W，MCLAREN D I.A new class of energy-preserving numerical integration methods［J］.Phys.A:Math.Theor，2008，41(4):1-7.

［9］MCLAREN R I，QUISPEL G R W，ROBIDOUX N.Geometric integration using discrete gradients［J］.Phil.Trans.R.Soc.Lond.A，1999，357(1754):1021-1045.

［10］CELLEDONI E，MCLACHLAN R I，OWREN B，et al.On conjugate B-series and their geometric structure［J］.Journal of Numerical Analysis，Industrial and Applied Mathematics，2010，5(1/2):85-94.

［11］CHARTIER P，FAOU E，MURUA A.An algebraic approach to invariant preserving integators:the case of quadratic and Hamiltonian invariants［J］.Numerische Mathematik，2006，103(4):575-590.