基于小波分析的盲源分离

林志阳，白 洋，张春元，易家傅

(海南大学 信息科学技术学院，海南 海口 570228)

盲信号分离(或称为盲源分离)是指从一系列混合信号中分离出原始信号的过程.这一过程可以不借助或很少借助相关源信号中的信息加以实现.典型的例子如“鸡尾酒会”问题，即假设许多人在一个房间里同时说话，而且还有人试图跟其中的一人讨论问题，这时很难完全听到每个人在说什么.笔者的方法是在不同位置上放一组传声器，各传声器所测到的信号是具有不同权重的原语音信号的混合信号，然后从接收的混合信号中分离和识别出原语音信号［1］.盲源分离常应用于语音信号分离与识别、数据通信与阵列信号处理、图像处理与识别以及文本分析与处理等［2］.

语音信号处理在通信和信号分析领域得到广泛应用，也用于噪声均衡、过滤、回声去除等.笔者通过小波去噪技术将混合信号中的噪声除去，是采用独立分量分析(ICA)方法，将录制的语音信号、音乐信号和混合信号，通过盲源分离将其在没有噪声背景的情况下分离出来.

1 盲信号处理

在“多输入-多输出”(MIMO)的非线性动态系统中，假定测到的传感器信号表示为x(t)=［x1(t)，x2(t)，…，xm(t)］T，则通过可逆系统，重构估计原始的源信号，s(t)=［s1(t)，s2(t)，…，sn(t)］T，盲信号输出为y(t)=［y1(t)，y2(t)，…，yn(t)］T［3］.其中，源信号s(t)未知，源信号如何混合得到观测信号也未知［1］，因此，可逆系统必须具有自适应性，即在非统计环境下具有若干跟踪能力，这种自适应性首先识别混合系统，然后利用未知源信号的独立性或稀疏性等先验知识，应用合适的优化算法估计出源信号(可逆系统并不能直接估计出源信号).在许多情况下，传感器信号是源信号的线性瞬时混合，即x(t)=H×s(t)，其中H 是混合矩阵，盲源分离可简化为求解矩阵W，使得y(t)=Wx(t)=s(t)，y(t)为源信号的一种估计和近似［1］.

对于盲源分离问题，在未知源信号和混合矩阵任何信息的情况下，只需假设信号是相互统计独立的，利用ICA 就能将源信号从混合矩阵中分离出来.盲信号分解的一般模式如图1 所示.n 个信号源s1，s2，…，sn所发出的信号被m 个传感器接收后产生输出x1，x2，…，xn.假设传输是瞬时的，即不同信号到达各个传感器的时间差可以忽略不计，并且传感器接收到的是各个信号源信号的线性混合［3］，即认为第i 个传感器的输出为

上式的矩阵表示为

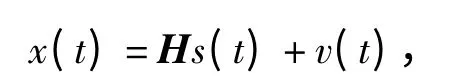
其中，x(t)=［x1(t)，x2(t)，…，xm(t)］T是混合信号向量，s(t)=［s1(t)，s2(t)，…，sn(t)］T是源信号列向量，v(t)=［v1(t)，v2(t)，…，vn(t)］T为传感器的观测噪声向量，H 是未知满秩的m×n 混合矩阵，hij为混合系数.换句话说，假设信号接收是通过传感器阵列实现的，那么，源信号就是各传感器信号的加权和.传感器阵列在语音信号的通信中是典型的时变、零均值、相互统计独立、完全未知的.

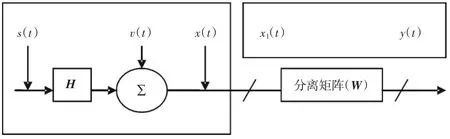
图1 盲信号分解系统

一般情况下，信号盲源分离是指在源信号未知，且混合系数hij未知的情况下，根据传感器所接收的混合信号x(t)对源信号向量s(t)或混合矩阵H 进行的估计.该问题也可表述为:在混合矩阵H 和源信号向量s(t)均未知的情形下，求一个n×m 的矩阵W，使W 对混合信号向量x(t)的线性变换

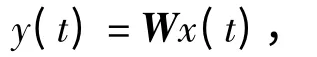
为对源信号向量s(t)或某些分量作一个估计［2］.

2 处理过程

2.1 离散小波变换去噪 离散小波变换是噪声信号去噪最简单高效的方法.本文小波去噪［5］是用阈值预处理法.从小波逆变换理论可知道，选择适当的小波尺度函数通常是最重要的.一般来说，去噪应用的小波尺度函数应与源信号有类似的特性.本文采用2 种不同的小波Daubechies 16 和32 进行研究.

在小波变换域中，可通过小波系数阈值收缩算法(例如非线性软阈值［5］)来完成去噪［6］.这种去噪方法由3 步组成:正交小波变换，非线性阈值收缩去噪，逆小波变换［4］.因为在变换域中系数是非线性收缩的，所以这种小波系数收缩［8］去噪算法是非线性的，它与其他完全线性的去噪方法是有区别的，因此，小波系数收缩去噪方法被认为是一种非参数方法.为了区别其他参数方法，笔者对特殊的模型进行了估计和假定［4］.

假定观测数据

其中S(t)为实际信号，N(t)为噪声，假定W(.)为小波变换，W-1(.)为逆小波变换，D(.λ)为软阈值去噪算子［6］.假定小波系数收缩去噪X(t)，S'(t)为S(t)的估计.以下分3 步来概括这个过程:

1)Y=W(X);

2)Z=D(Y，λ);

3)S'=W-1(Z).

2.2 独立分量分析 独立分量分析［9］就是将2 个源信号，利用独立和非高斯统计［6］原则分解成2 个混合信号.假定每个源信号的值在任意给定时间是一个随机变量，则每个源信号是统计独立的，也就是说，一个源信号的值与其他任何源信号的值是不相关的.

根据假设，ICA 可以将混合的源信号分离出来，这个算法只须将多个传感器信号作为输入信号，例如，传感器记录的2 个独立信号和2 个混合信号表示如下［8］

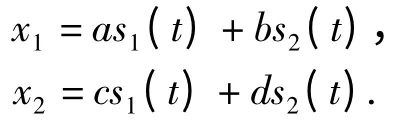
利用矩阵记号，多个混合信号可表示为

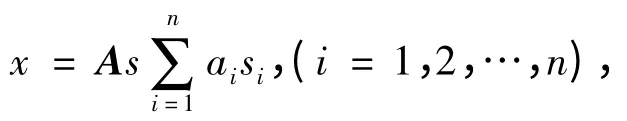
利用ICA 得到盲信号分离，这个过程是可逆的，假定混合信号x 作为输入，采用ICA 可以求得s，其中混合矩阵A 是可逆方阵，逆过程为

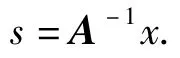
令W=A-1则s=Wx，即与BSS 问题相同.

假设一间房间里有2 个人同时说话，分别把2 个扬声器放在不同的地方，扬声器作为时间信号分别记为x1(t)和x2(t)，其中x1和x2表示振幅，t 表示时间，这些记录的信号是2 个扬声器发出的语音信号s1(t)和s2(t)的加权和

其中a11，a12，a12和a22参数取决于说话者与扬声器的距离和扬声器的特性.

使用记录信号x1(t)和x2(t)对于声源信号s1(t)和s2(t)的预测是合理的.时间延迟和其他因素被忽略都可以简化混合模型，可利用信号si(t)的统计特性来估计aii，实验证明，在每一时刻t，s1(t)和s2(t)是统计独立的.

2.3 离散小波变换与逆变换 利用小波变换分析信号常常是有效的.小波变换提供一种信号的时-频分布，即提供较高分辨率空间的频率信息和较低分辨率空间信号的时间分布信息，它不像傅里叶变换那样是一种完全的时-频变换.

离散小波变换可通过对信号的高通滤波器和低通滤波器［8］实现，如果g［t］和h［t］分别表示小波变换的高通滤波器和低通滤波器，则小波分解可以由下面的公式实现

其中，Yhigh［t］和Ylow［t］分别代表高频系数和低频系数.

为了得到离散小波系数［8］，将源信号进行重构，重构公式为

2.4 分离算法 盲信号分离过程如图2 所示，它由6 个部分组成.其中，输入信号采用混合信号，混合信号里的噪声采用小波去噪方法除去，然后通过DWT 进行分离，接着使用ICA 算法，再利用IDWT 进行重构，最后分离出源信号.

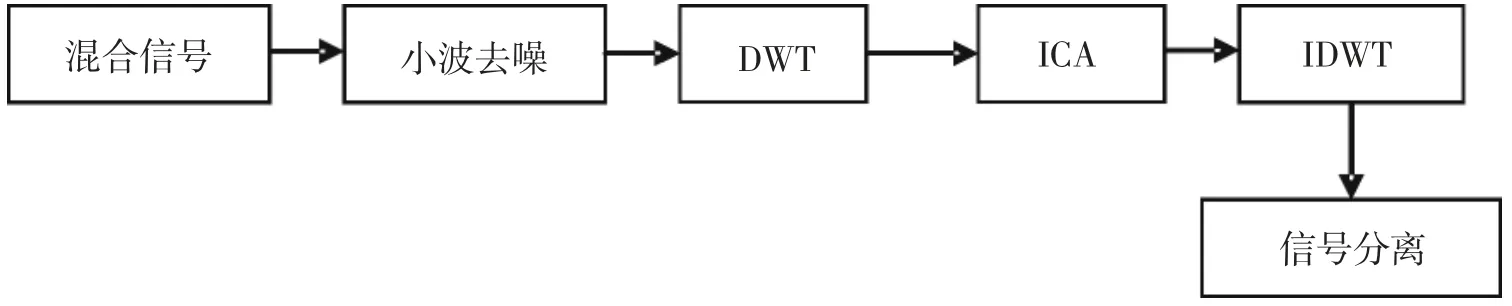
图2 盲信号分离框图

3 仿真结果

采用3 种不同的样本，即录制的语音信号、音乐信号和混合信号，分别采用2 种不同的方法进行仿真，一种是直接采用ICA 算法(如图3a，图4a，图5a)，另一种是笔者提出新的盲源分离算法(BSS)(如图3b，图4b，图5b)，并将小波变换技术和ICA 算法相结合，实现了较好的盲源分离.

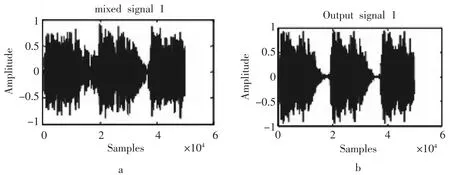
图3 录制的语音信号分解

图4 录制的音乐信号分解

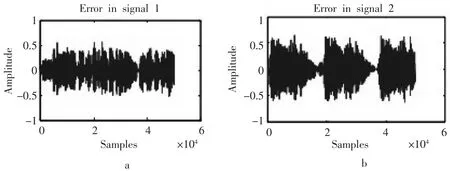
图5 2 种混合信号分解

4 小 结

笔者提出的新盲源(BSS)分离算法是在独立分量分析(ICA)算法中引入离散小波变换技术分解出有用的信号.该算法能够减少高阶统计量的相关性，有效地恢复源信号，与ICA 算法比较，BSS 算法更能够适用于盲信号分离问题.

［1］史习智.盲信号处理:理论与实践［M］.上海:上海交通大学出版社，2008.

［2］余先川，胡丹.盲源分离理论与应用［M］.北京:科学出版社，2011.

［3］YILMAZ O，RICKARD S.Blind separation of speech mixtures via timeFrequency masking［J］.IEEE transactions on signal processing，2004，52(7):207-215.

［4］POLIKAR Robi.The engineer's ultimate guide to wavelet analysis［J］.Hosted by Rowan University，College of Engineering Web Servers，2001，12(1):323-328.

［5］DONOHO D L.Denoising via soft thresholding［J］.IEEE Transactions on Information Theory，1995，5 (41):613-627.

［6］TASWELL Carl，COMPUTATIONAL Toolsmiths.What，Hoe，and Why of Wavelet Shrinkage Denoising［J］.Computing in Science ＆ Engineerng，2000，5(2):12-19.

［7］DONOHO D L，JOHNSTONE M Iain.Ideal spatial adaption via wavelet shrinkage［J］.Biometrika，1994，81(3):425-455.

［8］AAPO Hyvarinen，ERKKI Oja.Independent Component Analysis，Neural Networks［M］.New York :Academic Press，2000.