光纤绕制系统稳定张力控制策略研究＊

赵金才 王 中 高 卓 汤伟江

（1.中国船舶重工集团公司第七〇五研究所 西安 710075）（2.水下信息与控制重点实验室 西安 710075）

1 引言

以机电控制为主体的绕制张力控制系统，具有广泛的工业应用基础。目前，欧、美、日等世界先进工业制造强国都十分重视对稳定张力控制技术的研究，美国Rockwell Automation、3M 等数家公司，联合成立了张力技术研究中心，研究解决其工业生产中所涉及稳定张力控制等问题［1～3］。国内自上世纪80年代开展张力控制技术研究以来，在稳定张力控制方面提出了模糊免疫及自适应PID 等多种控制算法［4］。近年来，出现了许多用于生产绕制特定产品（如光纤环）的专用设备，这些设备技术成熟，在关键参数（如绕制张力）控制上方法多样、精度不断提高［11］。

本文针对光纤绕制的张力稳定控制要求（±5%精度），结合机电控制特性及系统工作原理设计了系统工作的控制策略。

2 系统介绍

该系统采用收线伺服电机速度控制和放线直流电机力矩控制方式相结合，如图1所示。主要由收线系统、放线系统、舞蹈轮、调节螺母、测量轮系及固定轮系组成。

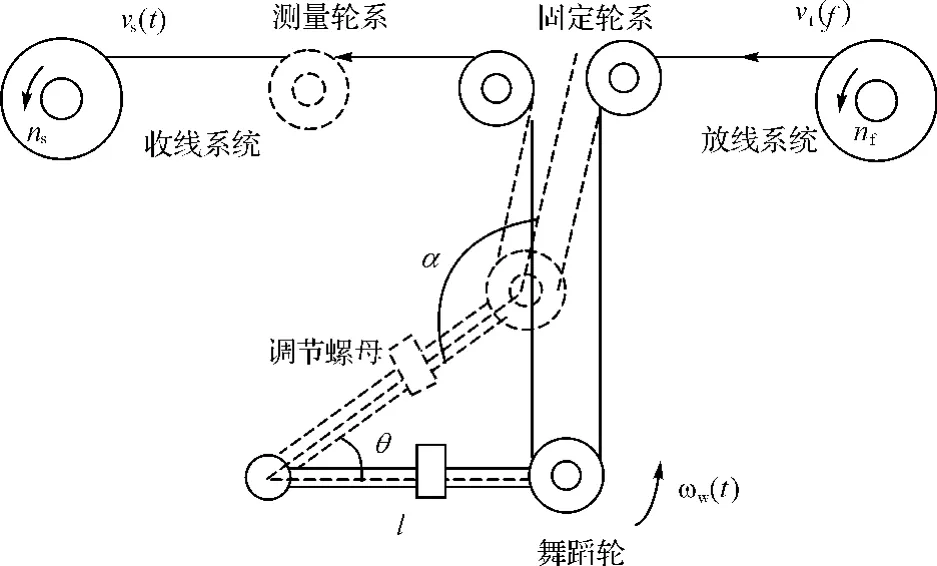
图1 光纤绕制系统结构示意图

稳定张力控制以舞蹈机构（由舞蹈轮、调节螺母等组成）为核心部件，其一端通过转轴与角度传感器相连并同轴固定在设备上，另一端同心安装多个转动轮，光纤依次绕过各转动轮后与收、放线盘相连。舞蹈轮机构的作用主要体现在两个方面：一是在结构上通过多重舞蹈轮设计延长了收放线间的线导光纤，为异常及突发工况下收放线间的速度响应提供了缓冲，实现了线团的安全绕制；二是通过控制舞蹈轮稳定在零位位置，可实现绕制过程中的张力稳定。此外，通过控制调节螺母在摆杆上的移动位置可消除由于动、静摩擦等因素引起的系统误差，从而实现线团以设定张力稳定绕制。

3 系统建模与仿真

通过图1简化相关结构，通过动力学分析可建立稳定张力控制的数学模型［2～5］，如式（1）

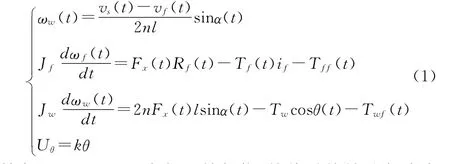
其中，ωw（t）、ωf（t）为舞蹈轮机构、放线系统转动角速度rad／s；vs（t）、vf（t）为收、放线速 度m／s；n为舞 蹈轮个数，l为舞蹈轮摆臂长度，m；Jf、Jw为放线系统及舞蹈轮机构转动惯量，kg·m2；Fx（t）为线上实时张力N；Rf（t）为放线盘实时半径，m；if为放线系统所选减速器减速比；Tf（t）、Tff（t）、Twf（t）、Tw为放线电机电磁 转矩、放 线系统及舞 蹈轮摩擦转矩和舞蹈轮重力矩，N·m；k为对应输入转角的比例系数，v／°。

根据系统模型建立稳定张力系统框图如图2所示［6］。其中，函数f（u1，θ）、f（u2，θ）分别是关于输入u1、u2和转角θ的函数，f（ω）、f（θ）分别是舞蹈轮转动角速度ωw和输出转角θ的函数，Bf、Bw分别是等效在放线电机主轴和舞蹈轮转动轴上的阻尼系数。

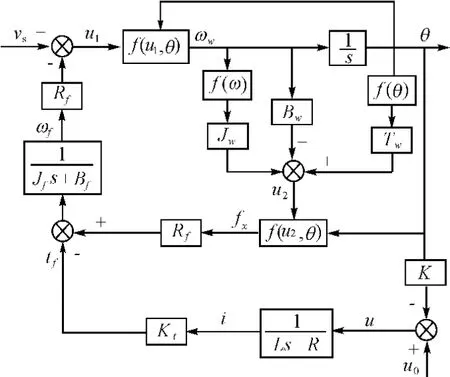
图2 稳定张力控制系统框图

当系统启动后放线电机根据力矩平衡将舞蹈轮机构稳定在零位位置，此时输出转角近似为零。在绕制开始时，收线电机首先响应，vs逐渐增大，此时收线速度大于放线速度，使得输出转角θ逐渐增大，进而增大线上张力；与此同时，放线系统根据θ变化引起的传感器输出控制放线电机的输入电压，实时调整放线电机的输出转矩，实现放线速度的随动控制，直至收线与放线等速运行；通过放线系统的力矩平衡控制，使输出转角逐步减小到零位附近，从而使线上张力逐步减小直至到达稳定。

在控制算法上，针对舞蹈轮转角不同，设计不同的PID控制参数形成基于专家经验的PID 控制算法［9］，其中张力仿真与试验对比曲线如图3所示，其中设定张力为3.2N。

2000年之前，日本的大学设立衍生风险企业数量很少，直到2001年经济产业省提出“大学衍生风险企业1 000家计划”，提出2002—2004年间设立1 000家衍生风险企业的目标后，才有了快速的增长并在2004年时达到顶峰，之后减少，直到2014年，随着产业竞争力强化法的实施，国立大学出资风险投资成为可能，大学衍生风险企业数量重新开始呈现上升趋势。根据经济产业省2017年的相关数据[10]，截至2017年11月，日本共有2 093家大学衍生风险企业，见图3。

可见，仿真与试验曲线变化趋势基本一致；但两者之间有一个稳定的差值，同时系统启动过程中有较大的张力超调，这些均与要求的光纤稳定张力绕制不符，故需设计系统工作的控制策略。

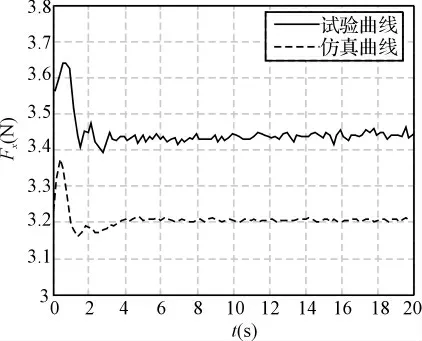
图3 张力Fx的仿真曲线与试验曲线对比

4 系统控制策略分析

4.1 延长收线速度上升时间策略

分析启动时的张力超调主要是由系统惯性引起的，考虑通过延长收线速度上升时间进而降低速度上升阶段的平均加速度值来减小张力超调［7］，速度控制示意图如图4所示。

其中Ⅰ为原设定的收线电机转速曲线，根据伺服电机特性，其单位时间内速度变化率相同，故要想将升速时间由tc延长至t′c，需对速度的变化进行步进控制，即在单次步进时间内输入定量的电压增量使速度逐步上升，如Ⅱ所示。其中tb为单次步进时间，nb为单次步进时间施加电压对速度的增加量。故在步进时间一定的情况下，通过控制单段电压的增量值，可控制速度的上升时间。

系统中针对不同的设定收线速度，可设置不同的速度上升时间，并据此设定单段时间的输入控制电压增量。

以设定速度为20m／min，张力3.2N 为例，进行仿真得张力变化曲线如图5所示。

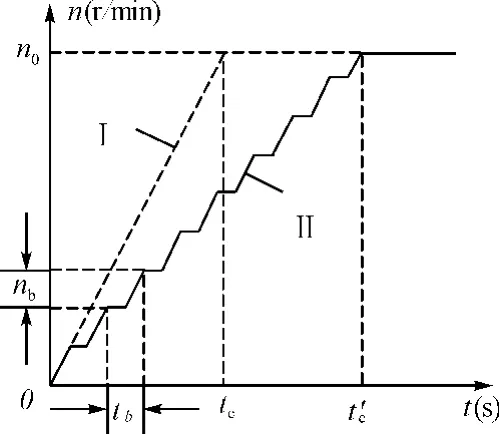
图4 延长收线电机速度上升时间示意图

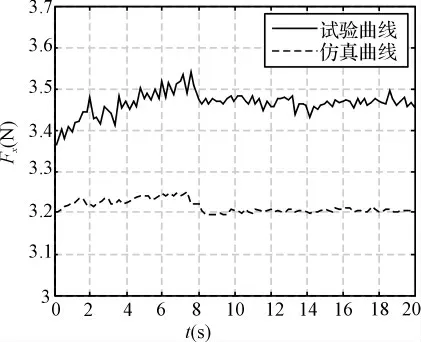
图5 延长速度上升时间输出张力Fx 仿真与试验曲线

可见，通过延长收线电机启动时间使张力在启动阶段的超调得到了较大的抑制，稳态时张力控制精度仅为1.84%，满足系统±5%的控制要求。但起始和稳态到达时的张力波动仍较为显著，这主要是由于线上加速度的突变引起的，故可考虑降低系统在起始和稳态到达时的平均加速度值来进一步降低启动过程的张力波动。

4.2 收线速度上升控制优化策略

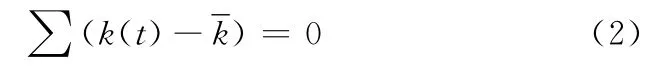
式中：k（t）为Ⅰ在t时刻加速度，m／s2；为Ⅱ升速段平均加速度，m／s2。

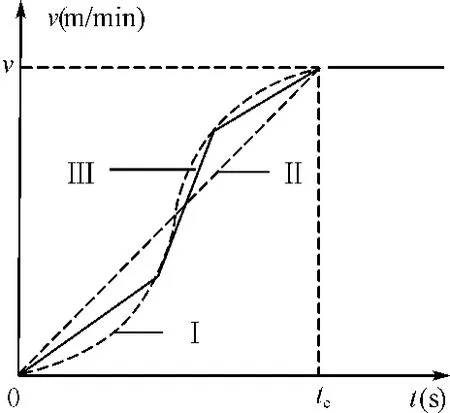
图6 上升速度优化曲线对比

若将收线的升速过程分为q段进行控制，则各段升速量与设定速度满足式（3）。

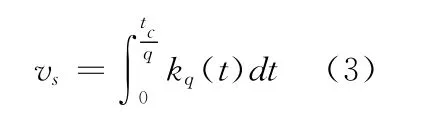
式中：tc为升速过程总时间，s；kq为分段线段的加速度，m／s2。

通过对各段选择合适的加速度，可使速度以既定的方式上升直至达到稳定，此时速度在上升阶段的控制算法如式（4）。

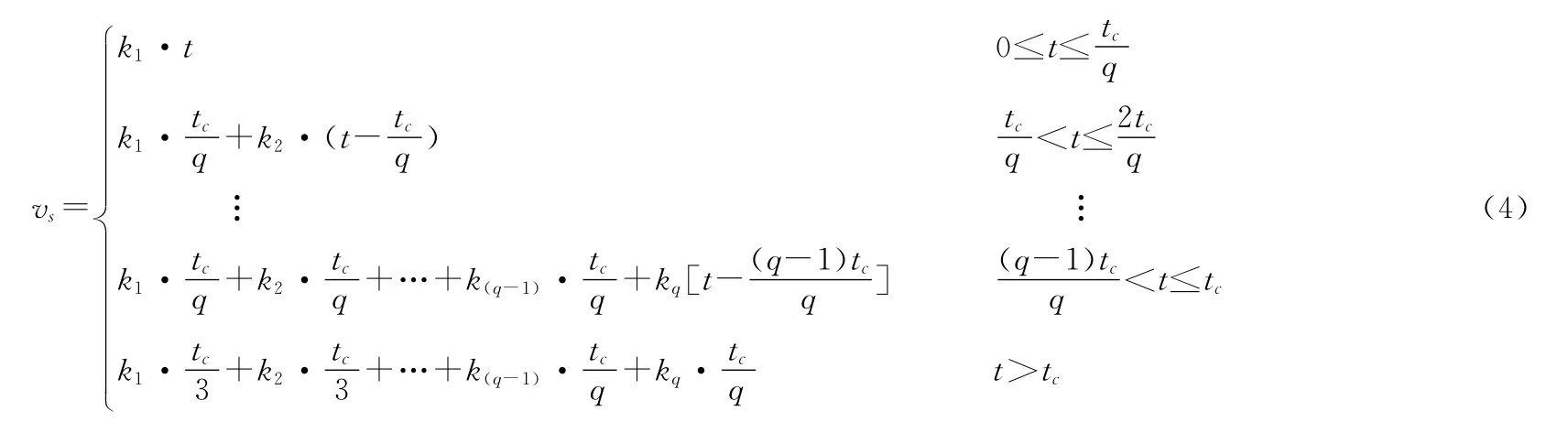
理论上，优化的控制曲线分段越多，则与理想曲线变化趋势越接近。实际中因为控制周期及电机响应延迟等因素的影响，使每段升速时间不宜过短，在上升总时间一定的情况下，决定了对升速时间的分段不宜过多。

4.3 张力实时调节控制策略

系统启动阶段的张力快速超调是由传动轮惯量和摩擦因素共同作用的结果，而稳态与设定张力的差值主要由摩擦作用产生，这些因素均为系统误差而无法直接消除［8］。根据舞蹈轮机构的设计（图1）可知，通过控制张力调节螺母在丝杠上的不同位置，即可由力矩平衡对线上张力的波动进行实时调整，从而实现对线团绕制张力的稳定控制。

通过对前述张力波动趋势分析知，在起始阶段，实际张力波动较设定值快速增大，直至达到稳态阶段后，张力波动逐渐减小。因此在控制张力调节螺母时应使起始阶段螺母以最大速度向支点方向移动，通过力矩平衡降低线上张力，直至张力达到设定值允许误差的范围后停止对螺母的移动控制。

根据设定绕制张力，绕制前使张力调节螺母处于有效行程中间位置。对螺母的移动控制采用如下策略：

1）给定控制频率控制螺母匀速快速运动，以降低系统延迟对速度的影响；

2）当实时张力波动超过设定范围后，对螺母进行移动控制；

3）当两次采样时刻的角度差值超出一定范围后，对螺母进行移动控制。

根据4.1仿真结果的分析，采用4.2的策略可降低系统起始和到稳定到达时的张力超调，采用4.3的策略可消除系统误差，据此对系统进行试验仿真，当绕制张力4N、设定速度为30m／min和50m／min时的张力变化曲线如图7所示。

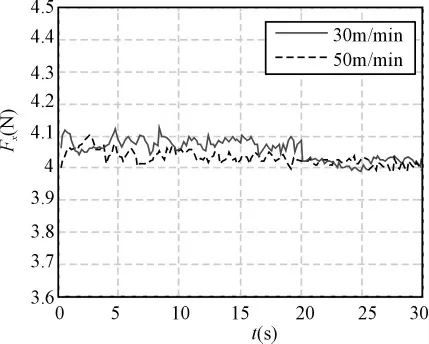
图7 协同控制时不同收线速度对应的张力变化曲线

图中，当速度为30m／min和50m／min时的启动阶段张力超调分别为2.49%和2.53%，稳态张力控制精度分别0.73%和1.09%，可见启动和稳态张力控制精度均得到较大提高，完全满足系统的控制要求。

5 结语

本文根据介绍的光纤稳定张力绕制系统，在对仿真结果分析的基础上，提出基于收线速度优化和张力实时调节的控制策略。实践表明，采用该策略后可将启动张力控制在±3%以内，稳态张力控制在±1.5%以内，优于系统±5%的稳态张力设计要求。故该控制策略有效，实现了预期的控制目标。

［1］郭帅，何永义，姚志良，等.张力控制试验平台及监测系统研究［J］.工业仪器与自动化装置，2005，74（6）：42－45.

［2］赵金才，王中，高卓，等.基于稳定张力的光纤绕制系统建模与仿真［J］.舰船科学技术，2013，23（2）：88－92.

［3］Ku Chin Lin.Observer－Based Tension Feedback Control With Friction and Inertia Compensation［J］.IEEE Transaction on Control System Teehnology，2003，11（l）：109－118.

［4］Ku Chin Lin，Ming－Ching Tsai and Kung－Yi Chen.Web Tension Control of a Start－up Process using Observer Techniques with Friction and Inertia Compensation［J］.The 27th Annual Conference of the IEEE Industrial Electronics Society，2001，9（5）：37－42.

［5］高钟毓.机电控制工程［M］.北京：清华大学出版社，2011：54－58.

［6］薛定宇，陈阳泉.基于MATLAB／Simulink的系统仿真技术与应用［M］.北京：清华大学出版社，2011，2：175－198.

［7］鄢景华.自动控制原理［M］.哈尔滨：哈尔滨工业大学出版社，2000，7：35－41.

［8］刘金昆.先进PID控制及MATLAB仿真［M］.北京：电子工业出版社，2011，3：223－225.

［9］J.C.Basilio，S.R.Matos.Design of PI and PID Controllers With Transient Performance Specification［J］.IEEE Transactions On Education，2002，4（6）：97－99.

［10］姜黎，高志军，曹新星.基于光纤通信技术的数据单向传输设备研究［J］.计算机与数字工程，2012（3）.

［11］赵晋洪，舒晓武.光纤绕线机张力控制系统的研究［J］.光学仪器，2005，04：64－68.