分布式融合处理结构研究＊

李 岳

（中国电子科技集团公司第二十八研究所 南京 210007）

1 引言

目前，分布式融合系统［1～3］中普遍采用两种融合处理结构，一种是原始航迹与融合航迹之间的融合，另一种是原始航迹与原始航迹之间的融合，这两种融合处理结构各有优缺点，需要针对具体问题进行深入分析。关于第一种融合处理结构的优点是，它以融合航迹作为中心线贯穿整个融合相关过程，逻辑控制比较简单，容易掌控。但其缺点是在融合过程中往往忽略了误差的相关性，破坏了算法的前提假设，以导致算法性能下降。而第二种融合处理结构的优点是，其相互参加融合的数据源具有独立性，能较好地满足或近似满足算法的先决条件，使得算法性能能够得到充分的发挥。但其缺点是这种融合处理结构考虑的因素较多，导致融合处理逻辑、航迹管理比较复杂，难以实现。

本文针对分布式融合系统中的两种融合处理结构的使用问题，通过理论推导，深入分析，寻求一种简单而又能充分发挥算法性能的融合处理结构，为分布式融合系统提高融合性能奠定一定的基础。

2 分布式融合处理结构

分布式融合系统就是，每个传感器的检测报告在进入融合之前，先由它自己的数据处理器产生局部多目标跟踪航迹，然后把处理后的信息送至融合中心，融合中心根据各节点的航迹数据完成航迹关联和航迹融合，形成全局估计。相对于集中式系统，分布式融合系统所要求的通信开销小，融合中心计算机所需的存储容量小，且融合速度快。

首先为了下面的讨论方便，在这里，引入两个术语，即原始航迹和融合航迹。

定义1 在多传感器融合系统中，每个传感器的目标跟踪器所给出的航迹称为原始航迹。

定义2 航迹融合系统将各个传感器的输入的原始航迹经过相关判定、融合后形成的航迹称为融合航迹。当然，将原始航迹与融合航迹融合后形成的航迹仍然称为融合航迹。

如下图所示，各个模块组成了一个航迹融合系统。

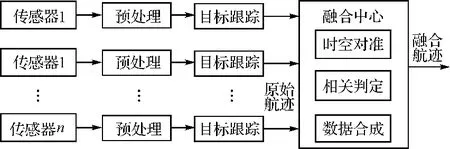
图1 分布式航迹融合系统

根据图1，各个传感器跟踪器产生自身的原始航迹，然后，各传感器将周期性探测的原始航迹传送到融合中心进行融合。融合中心处理主要包含三个步骤：时空对准、相关判定以及数据合成。

在这里，融合航迹得到之前，需要考虑一个融合处理结构的问题，是采用原始航迹与原始航迹之间的融合，还是原始航迹与融合航迹之间的融合？关于这两种融合处理结构存在何区别，对融合的影响有多大？下面将进一步进行探讨。

2.1 假设基础

2.2 原始航迹与融合航迹之间的融合

原始航迹与融合航迹之间的融合是现在普遍采用的一种融合处理结构，它的优点就是以融合航迹为航迹相关主线，贯穿整个相关逻辑，实现比较简单，容易掌控，但是这种融合处理结构也存在诸多缺点，具体如下。

原始航迹与融合航迹之间的融合主要是当原始航迹到来时，把融合航迹的前一时刻的状态外推到接受原始航迹的时刻，并与新来的原始航迹进行相关融合，得到当前的融合航迹的状态估计，形成融合航迹的新成员。然而，这样必须要面对一个相关估计误差的问题，这也是往往忽略的一个问题，也是算法性能难以发挥到理论水平的症结所在。进一步说，由于相关或融合中过去处理误差导致了融合航迹中的任何误差会影响将来的融合性能。如图2所示，对于这种结构，我们也可以看出融合航迹存在先验的公共信息源，前后点存在一定的关联，所以先验信息在这里是不能忽略掉的。

图2 原始航迹与融合航迹融合

由于融合航迹的状态估计包括了航迹的先验信息，所以在使用这种处理结构的时候要想算法性能充分地发挥必须采用“去相关”算法［4～7］，将相关误差消除，否则融合能力将会大打折扣。

信息去相关可以使用Kalman滤波器的信息滤波器形式去推导，其关键思想是识别用来融合的两个估计量中的相同信息，为了避免重复计算，必须在融合的时候去除掉。

则有：

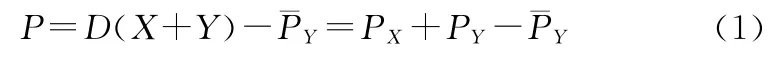
其中是传感器上一次传给融合航迹的误差协方差（传播到相同的融合时刻），这就是融合算法用到的附加信息。

这种方法对这种融合处理结构是非常有用的。这种方法没有过程噪声是最优的。当过程噪声很小，并且原始航迹的更新速率相当高时，表现出的性能下降也是很小的。

2.3 原始航迹与原始航迹之间的融合

由于上面的处理结构考虑的因素较多，能否有一种处理结构考虑的因素较少，而且又能使算法性能很好地发挥呢？原始航迹与原始航迹之间的融合，就能很好地满足上面两个条件，但实现起来稍显麻烦，因为这种处理结构贯穿整个相关逻辑的是相关对照表，再根据相关对照表的信息对对应批号的原始航迹进行相关和合成，而融合航迹不参加相关和合成，只是数据分发的对象。

原始航迹之间的融合主要是对多个不同传感器的原始航迹在数据对准后的状态估计进行关联和融合得到融合航迹的状态估计。在这一融合结构中航迹融合没有利用前一时刻的融合航迹的状态估计，所以不涉及相关估计误差问题。

因为原始航迹基本上是一个无记忆的操作，所以关联和融合的误差不会从一个时刻传播到下一个时刻。如下图所示，对于这种结构，我们可以看到融合航迹仅仅只是来自多个原始航迹的集合，不存在前后点之间的关联，所以也就没有共同的先验信息。由于融合航迹的状态估计不代入下一次融合，这原始航迹｛X｝ 和｛Y｝ 一般情况下是相互独立的，则有：

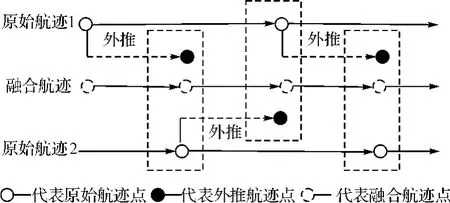
图3 原始航迹与原始航迹融合

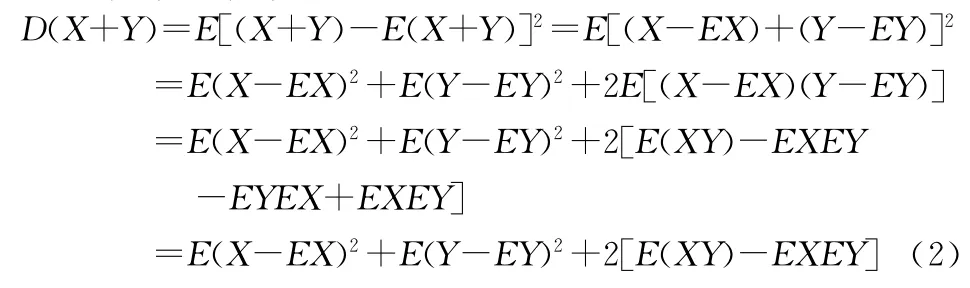
由于｛X｝ 和｛Y｝ 相互独立，则有：

所以有：

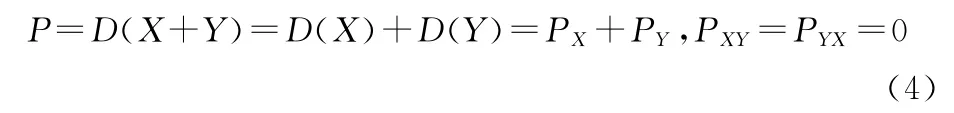
采用这种融合处理结构可以不必考虑误差的相关性问题，这样对相关判别和数据合成是个很好的先决条件（一般认为不同传感器之间的测量是相互独立的，并且呈正态分布或近似正态分布）。

2.4 公共的过程噪声

这种情况发生在传感器不共享共同的量测而进行融合时。当目标动态方程不确定时，给定某一时刻的目标状态，来自两条传感器的原始航迹不一定条件独立。如此，形成的公共的过程噪声就会使得这两条原始航迹的估计误差可能不独立。这种情况，在上面2.2节、2.3节均有可能发生。

所以当各个传感器的估计误差是相关的时候，如果不考虑PXY的存在，任何算法效果都会是次优的。下面给出一种方法推导：

当采用Kalman滤波器作为估计器的时候，其中的互协方差［8～9］可以由下式得到：

其中K是Kalman滤波器增益，Φ是状态转移矩阵，Q是噪声协方差矩阵，H是观测矩阵。

得到PXY的优点是，考虑了各个传感器估计误差之间的相关性，很好地控制公共的过程噪声。如果所关心的系统是线性不变的，则互协方差阵就可以离线进行计算。

3 数值试验

仿真实验在某型多源信息融合系统仿真平台上完成，利用相同的剧情和雷达数据分别采用第一种融合处理结构和第二种融合处理结构进行了仿真比较。设雷达1大地坐标为（116.4，21.8，0.0），雷达2大地坐标为（117.1，21.9，0.0），两探测平台速度均为8m／s，向正北行驶；两雷达量测误差分布服从N（0，σ2），距离误差σd分别为30m、80m，方位误差σα分别为0.1°、0.3°，仰角误差分别是0.1°、0.2°，采样周期分别为1.5s和2s。模拟仿真三批目标：目标1初始大地坐标为（116.162，22.9391，3000.0），目标2 初始大地坐标为（116.162，22.9341，3000.0），目标3初始大地坐标为（116.162，22.9291，3000.0）；三批目标间距650m，同时做匀速直线运动，航速均为119m／s，航向均为135°，仿真测试100周期。具体情况如下图所示。

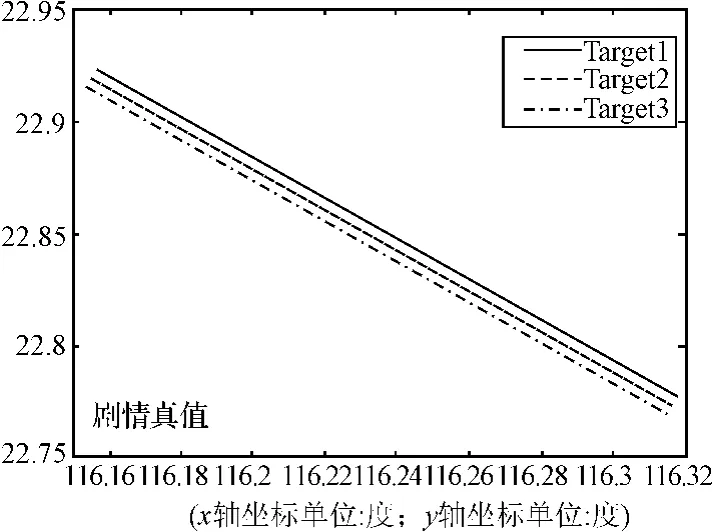
图4 剧情真值目标运动经度、纬度图

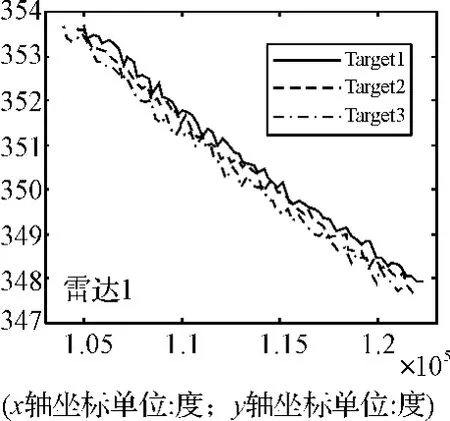
图5 雷达1探测目标距离、方位图

图6 雷达2探测目标距离、方位图

图7 原始航与原始航迹融合目标经度、纬度图

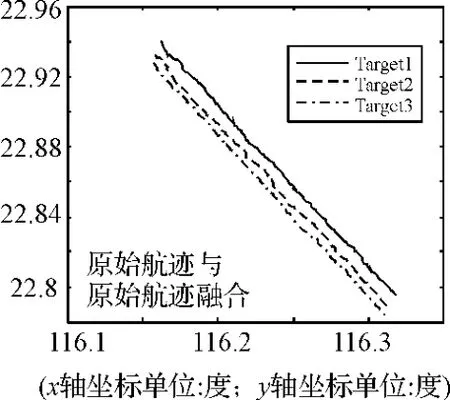
图8 原始航迹与融合航迹融合目标经度、纬度图

融合目标质量性能评价标准采用融合航迹精度［12］指标：

融合航迹精度指标主要是反映融合系统输出融合航迹的质量。在本次仿真实验中，各目标的融合航迹精度计算结果如表1。

表1 融合航迹精度计算结果

可见，原始航迹之间的融合处理精度要略高于原始航迹与融合航迹之间的融合处理精度，主要原因是原始航迹与融合航迹之间的融合忽略了误差的相关性。

4 结语

综上所述，从上面对两种融合处理结构的分析，可以得出结论，如果充分考虑融合的误差因素，包括公共过程噪声、误差相关性等，这两种融合处理结构都能满足情报系统的数据融合要求，但是融合的误差因素是复杂多变的，难以进行正确的把握，所以寻求一种简单的而又能充分发挥算法性能的融合处理结构是非常必要的，通过大量的数据实验和理论分析，第二种融合处理结构（原始航迹之间的融合）是比较实用的，在当前分布式融合系统中的应用也是较成功的。

［1］Mutambara A G O.Decentralized Estimation and Control for Multisensor Systems［M］.Boca Raton：CRC Press，1998.

［2］杨万海.多传感器数据融合及其应用［M］.西安：西安电子科技大学出版社，2004.

［3］何友，王国宏，彭应宁，等.多传感器信息融合及应用［M］.第二版.北京：电子工业出版社，2007.

［4］Chong C Y.Hierarchical estimation［C］／／Proc.MIT／ONR Workshop on C3.Monterey，CA，1979.

［5］LiggIns M E.Distributed fusion architectures and algorithms for target tracking［C］／／Proceedings of the IEEE，1997，85（1）：95－107.

［6］Chong C Y.Mori S，Chang K C.Information fusion in distributed sensor network［C］／／Proc.1985American Control Conference.New York，NY，USA：IEEE，1985：830－835.

［7］Chong C Y.Distributed fusion architetures and algorithms［C］／／Pro.1998International Conf.on Multisource－Multisensor Data Fusion，1998：95－107.

［8］Xia Xiang－Gen.Discrete chirp－Fourier transform and its application to chirp rate estimation［C］／／IEEE Trans.SP（s1053－587X），2000，48（11）：3122－3133.

［9］［澳］安德森BDO，等.最佳滤波［M］.北京：国防工业出版社，1983.

［10］胡敏，王梅.分布式虚拟现实中数据分发管理算法研究［J］.计算机与数字工程，2011，（1）.

［11］王莹，陈涛.基于组件的分布式测试管理系统研究［J］.计算机与数字工程，2011，（8）.

［12］周永丰，吴汉宝.雷达数据相关器的基本性能测试方法［J］.舰船电子工程，2005，25（1）：35－40.